JEE Advanced (Subjective Type Questions): Modern Physics- 1 | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. A single electron orbits around a stationary nucleus of charge + Ze. Where Z is a constant and e is the magnitude of the electronic charge. It requires 47.2 eV to excite the electron from the second Bohr orbit to the third Bohr orbit.
Find (1981- 10 Marks)
(i) The value of Z.
(ii) The energy required to excite the electron from the third to the fourth Bohr orbit.
(iii) The wavelength of the electromagnetic radiation required to remove the electron from the first Bohr orbit to infinity.
(iv) The kinetic energy, potential energy, potential energy and the angular momentum of the electron in the first Bohr orbit.
(v) The radius of the first Bohr orbit.
(The ionization energy of hydrogen atom = 13.6 eV, Bohr radius = 5.3 × 10–11 metre, velocity of light = 3 × 108 m/sec.
Planck’s constant = 6.6 × 10–34 joules - sec).
Ans. (i) 5
(ii) 16.53 eV
(iii) 3.65 × 10–9 m
(iv) 340 eV, –680 eV, 1.05 × 10–34 J.s
(v) 1.05 × 10–11m
Solution.
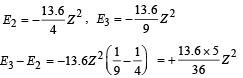
But E3 – E2 = 47.2 eV (Given)
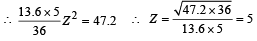
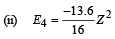
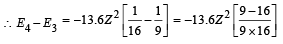
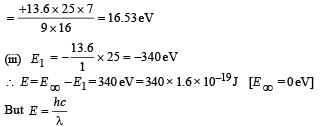
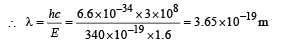
(iv) Total Energy of 1st orbit = – 340 eV We know that – (T.E). = K.E. [in case of electron revolving around nucleus] and 2T.E. = P.E.
∴ K.E. = 340 eV ; P.E. = – 680 eV
KEY CONCEPT :
Angular momentum in 1st orbit :
According to Bohr’s postulate,
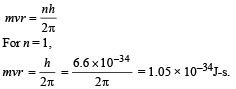
(v) Radius of first Bohr orbit
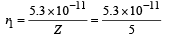
= 1.06 × 10–11 m
Q.2. Hydrogen atom in its ground state is excited by means of monochromatic radiation of wavelength 975Å. How many different lines are possible in the resulting spectrum ?
Calculate the longest wavelength amongst them. You may assume the ionization energy for hydrogen atom as 13.6 eV. (1982 - 5 Marks)
Ans. 6, 18.835 × 10–7 m
Solution.
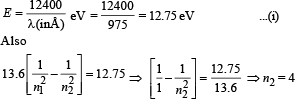
For every possible transition one downward arrow is shown therefore the possibilities are 6.
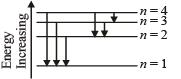
Note : For longest wavelength, the frequency should be smallest.
This corresponds to the transition from n = 4 to n = 3, the energy will be 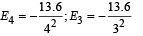
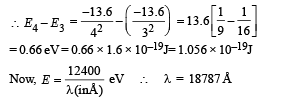
Q.3. How many electron, protons and neutr ons are th ere in a nucleus of atomic number 11 and mass number 24 ? (1982 - 2 Marks)
(i) number of electrons =
(ii) number of protons =
(iii) number of neutrons =
Ans. 0, 11, 13
Solution. (i) In a nucleus, number of electrons = 0 (∵electrons don't reside in the nucleus of atom).
(ii) number of protons = 11
(iii) number of neutrons = 24 – 11 = 13
Q.4. The ionization energy of a hydrogen like Bohr atom is 4 Rydbergs. (i) What is the wavelength of the radiation emitted when the electron jumps from the first excited state to the ground state ? (ii) What is the radius of the first orbit for this atom? (1984- 4 Marks)
Ans. (i) 300Å (ii) 2.5 × 10–11 m
Solution.
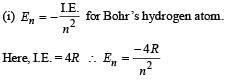
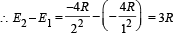 ..(i)
..(i)
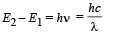 ..(ii)
..(ii)
From (i) and (ii)
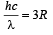
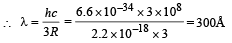
(ii) The radius of the first orbit
Bohr’s radius of hydrogen atom = 5 × 10–11 m (given)
| En| = + 0.22 × 10–17Z2 = 4R = 4 × 2.2 × 10–18
∴ Z = 2
Q.5. A double ionised Lithium atom is hydrogen-like with atomic number 3. (1985 - 6 Marks)
(i) Find the wavelength of the radiation required to excite the electron in Li++ from the first to the third Bohr orbit. (Ionisation energy of the hydrogen atom equals 13.6 eV.)
(ii) How many spectral lines ar e observed in the emission spectrum of the above excited system?
Ans. (i) 1.142 × 10–8
(ii) 3
Solution.
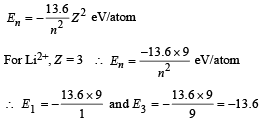
ΔE = E3 – E1 = – 13.6 – (–13.6 × 9)
= 13.6 × 8 = 108.8 eV/atom
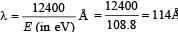
(ii) The spectral line observed will be three namely 3 → 1, 3 → 2, 2 → 1.
Q.6. A triode has plate characteristics in the form of parallel lines in the region of our interest. At a grid voltage of – 1 volt the anode current I (in milli amperes) is given in terms of plate voltage V (in volts) by the algebraic relation : I = 0.125V – 7.5
For grid voltage of – 3 volts, the current at anode voltage of 300 volts is 5 milliampere. Determine the plate resistance (rp), transconductance (gm) and the amplification factor (µ) for the triode. (1987 - 7 Marks)
Ans. 8 mΩ, 12.5 × 10–3 s,100
Solution. I = 0.125 V – 7.5
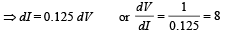
We know that plate resistance, 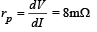
The transconductance, 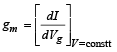
At Vg = – 1 volt, V = 300 volt, the plate current
I = [0.125 × 300 – 7.5] mA = 30 mA
Also it is given that Vg = – 3V, V = 300 V and I = 5mA
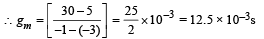
The characteristics are given in the form of parallel lines. Amplification factor
= rp gm = 8 × 103 × 12.5 × 10–3 = 100
Q.7. A particle of charge equal to that of an electron, – e, and mass 208 times the mass of the electron (called a mu-meson) moves in a circular orbit around a nucleus of charge + 3e. (Take the mass of the nucleus to be infinite). Assuming that the Bohr model of the atom is applicable to this system. (1988 - 6 Marks)
(i) Derive an expression for the radius of the nth Bohr orbit.
(ii) Find the value of n for which the radius of the orbit is approximately the same as that of the first Bohr orbit for the hydrogen atom.
(iii) Find the wavelength of the radiation emitted when the mu-meson jumps from the third orbit of the first orbit.
Ans.
Solution. (i) Let m be the mass of electron. Then the mass of mumeson is 208 m. According to Bohr’s postulate, the angular momentum of mu-meson should be an integral multiple of h/2π.
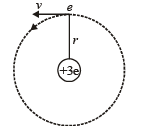
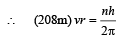
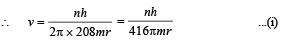
Note: Since mu-meson is moving in a circular path, therefore, it needs centripetal force which is provided by the electrostatic force between the nucleus and mumeson.
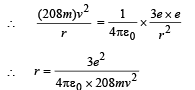
Substituting the value of v from (1), we get
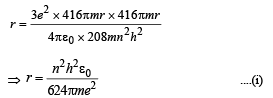
(ii) The radius of the first orbit of the hydrogen atom
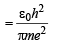 ...(ii)
...(ii)
To find the value of n for which the radius of the orbit is approximately the same as that of the first Bohr orbit for hydrogen atom, we equate eq. (i) and (ii)
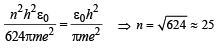
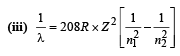
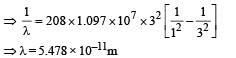
Q.8. A gas of identical hydrogen-like atoms has some atoms in the lowest (ground) energy level A and some atoms in a particular upper (excited) energy level B and there are no atoms in any other energy level. The atoms of the gas make transition to a higher energy level by absorbing monochromatic light of photon energy 2.7 eV. Subsequently, the atoms emit radiation of only six different photon energies. Some of the emitted photons have energy 2.7 eV, some have energy more and some have less than 2.7 eV. (1989 - 8 Marks)
(i) Find the prin cipal quantum number of the initially excited level B.
(iii) Find the ionization energy for the gas atoms.
(iii) Find the maximum and the minimum energies of the emitted photons.
Ans. (i) 2
(ii) 14.46 eV
(iii) 13.5 eV, 0.7 eV
Solution. (i) The transition state of six different photon energies are shown.
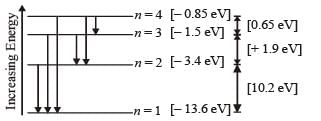
Since after absorbing monochromatic light, some of the emitted photons have energy more and some have less than 2.7 eV, this indicates that the excited level B is n = 2. (This is because if n = 3 is the excited level then energy less than 2.7 eV is not possible).
(ii) For hydrogen like atoms we have
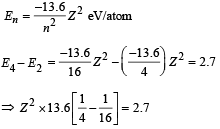
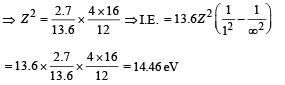
(iii) Max. Energy
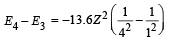
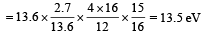
Min. Energy
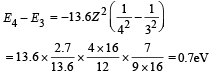
Q.9. Electron s in hydrogen like atom (Z = 3) make transitions from the fifth to the fourth orbit and from the fourth to the third orbit. The resulting radiations are incident normally on a metal plate and eject photoelectrons. The stopping potential for the photoelectrons ejected by the shorter wavelength is 3.95 volts. Calculate the work function of the metal and the stopping potential for the photoelectrons ejected by the longer wavelength. (1990 - 7 Marks)
(Rydberg constant = 1.094 × 10 7 m -1 )
Ans. 2 eV, 0.754 V
Solution. For hydrogen like atom energy of the nth orbit is
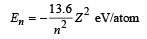
For transition from n = 5 to n = 4,
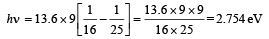
For transition from n = 4 to n = 3,
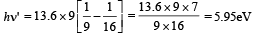
For transition n = 4 to n = 3, the frequency is high and hence wavelength is short.
For photoelectric effect, hn' – W = eV0, where W = work function
5.95 × 1.6 × 10–19 – W = 1.6 × 10–19 × 3.95
⇒ W = 2 × 1.6 × 10–19 = 2 eV
Again applying hn – W = eV'0
We get, 2.754 × 1.6 × 10–19 – 2 × 1.6 × 10–19 = 1.6 × 10–19 V'0
⇒ V'0 = 0.754 V
Q.10. It is proposed to use the nuclear fusion reaction 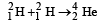 in a nuclear reactor of 200 MW rating. If the energy from the above reaction is used with a 25 per cent efficiency in the reactor, how many grams of deuterium fuel will be needed per day. (The masses of
in a nuclear reactor of 200 MW rating. If the energy from the above reaction is used with a 25 per cent efficiency in the reactor, how many grams of deuterium fuel will be needed per day. (The masses of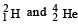 are 2.0141 atomic mass units and 4.0026 atomic mass units respectively)
are 2.0141 atomic mass units and 4.0026 atomic mass units respectively)
Ans. 119.6 gm
Solution. Energy required per day
E = P × t = 200 × 106 × 24 × 60 × 60
= 1.728 × 1013J
Energy released per fusion reaction
= [2 (2.0141) – 4.0026] × 931.5 MeV
= 23.85 MeV = 23.85 × 106 × 1.6 × 10–19
= 38.15 × 10–13J
∴No. of fusion reactions required
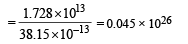
∴ No. of deuterium atoms required
= 2 × 0.045 × 1026 = 0.09 × 1026
Number of moles of deuterium atoms
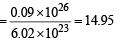
∴ Mass in gram of deuterium atoms
= 14.95 × 2 = 29.9 g
But the efficiency is 25%.
Therefore, the actual mass required = 119.6 g
Q.11. A monochromatic point source radiating wavelength 6000 Å, with power 2 watt, an aperture A of diameter 0.1 m and a large screen SC are placed as shown in fig. A photoemissive detector D of surface area 0.5 cm2 is placed at the centre of the screen. The efficiency of the detector for the photoelectron generation per incident photon is 0.9. (1991 - 2 + 4 + 2 Marks)
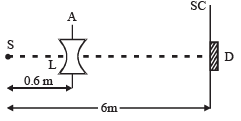
(a) Calculate the photon flux at the centre of the screen and the photocurrent in the detector.
(b) If the concave lens L of focal length 0.6 m is inserted in the aperture as shown, find the new values of photon flux and photocurrent. Assume a uniform average transmission of 80% from the lens.
(c) If the work function of the photoemissive sur face is 1eV, calculate the values of the stopping potential in the two cases (without and with the lens in the aperture).
Solution. Energy of one photon 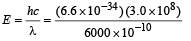
= 3.3 × 10–19 J
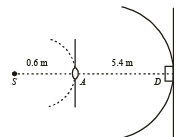
Power of the source is 2 W or 2 J/s. Therefore, number of photons emitting per second,
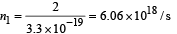
At distance 0.6 m, number of photons incident per unit area per unit time :
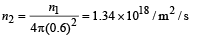
Area of aperture is,
∴ Total number of photons incident per unit time on the aperture,
n3 = n2s1 = (1.34 × 1018) (7.85 × 10-3) / s
= 1.052 × 1016 / s
The aperture will become new source of light.
Now these photons are further distributed in all directions.
Hence, at the location of detector, photons incident per unit area per unit time :
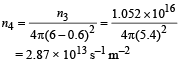
This is the photon flux at the centre of the screen. Area of detector is 0.5 cm2 or 0.5 × 10–4 m2. Therefore, total number of photons incident on the detector per unit time :
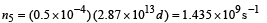
The efficiency of photoelectron generation is 0.9. Hence, total photoelectrons generated per unit time :
n6 = 0.9n5 = 1.2915 × 109 s-1
or, photocurrent in the detector :
i = (e)n6 = (1.6 × 10-19) (1.2915 × 109) = 2.07 × 10-10 A
(b) Using the lens formula :
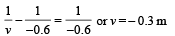
i.e., image of source (say S', is formed at 0.3 m from the lens.)
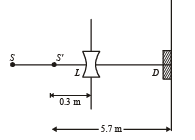
Total number of photons incident per unit time on the lens are still n3 or 1.052 × 1016/s. 80% of it transmits to second medium. Therefore, at a distance of 5.7 m from S' number of photons incident per unit are per unit time will be :
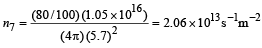
This is the photon flux at the detector.
New value of photocurrent is :
i = (2.06 × 1013) (0.5 × 10-4) (0.9) (1.6× 10-19)
= 1.483 × 10–10 A
(c) For stopping potential
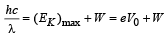
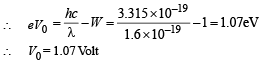
Note : The value of stopping potential is not affected by the presence of concave lens as it changes the intensity and not the frequency of photons. The stopping potential depends on the frequency of photons.
Q.12. A nucleus X, initially at rest, undergoes alpha decay according to the equation, 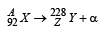
(a) Find the values of A and Z in the above process.
(b) The alpha particle pr oduced in the above process is found to move in a circular track of radius 0.11 m in a uniform magnetic field of 3 Tesla. Find the energy (In MeV) released during the process and the binding energy of the parent nucleus X.
Given that : m(Y) = 228.03 u; m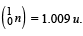
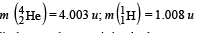
Ans. (a) 232, 90
(b) 5.34 MeV, 1823 MeV
Solution. 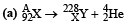
A = 228 + 4 = 232; 92 = Z + 2 ⇒ Z = 90
(b) Let v be the velocity with which α - particle is emitted.
Then
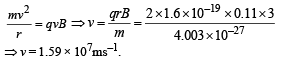
Applying law of conservation of linear momentum during α-decay we get
mY vY = mαvα ...(1)
The total kinetic energy of α-particle and Y is
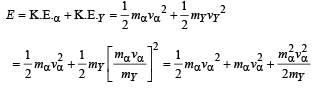
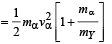
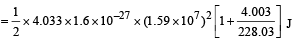
= 8.55 × 10–13 J
= 5.34 MeV
∴ Mass equivalent of this energy
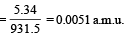
Also, mx = mY + mα + mass equivalent of energy (E)
= 228.03 + 4.003 + 0.0057 = 232.0387 u.
The number of nucleus = 92 protons + 140 neutron.
∴ Binding energy of nucleus X
= [92 × 1.008 + 140 × 1.009] – 232.0387
= 1.9571 u = 1.9571 × 931.5
= 1823 MeV.
Q.13. Light from a discharge tube containing hydrogen atoms falls on the surface of a piece of sodium. The kinetic energy of the fastest photoelectrons emitted from sodium is 0.73 eV. The work function for sodium is 1.82 eV. Find (1992 - 10 Marks)
(a) the energy of the photons causing the photoelectric emission,
(b) the quantum numbers of the two levels involved in the emission of these photons,
(c) the change in the angular momentum of the electron in the hydrogen atom in the above transition, and
(d) the recoil speed of the emitting atom assuming it to be at rest before the transition. (Ionization potential of hydrogen is 13.6 eV)
Ans. (a) 2.55 eV (b) 4 → 2
(d) 0.814 m/s
Solution. (a) The energy of photon causing photoelectric emission
= Work function of sodium metal + KE of the fastest photoelectron
= 1.82 + 0.73 = 2.55 eV
(b) We know that 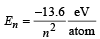 for hydrogen atom.
for hydrogen atom.
Let electron jump from n2 to n1 then
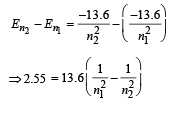
By hit and trial we get n2 = 4 and n1 = 2
[angular momentum mvr = nh/2π]
(c) Change in angular momentum
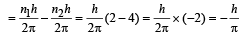
(d) The momentum of emitted photon can be found by de Broglie relationship
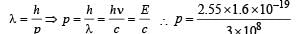
Note : The atom was initially at rest the recoil momentum of the atom will be same as emitted photon (according to the conservation of angular momentum).
Let m be the mass and v be the recoil velocity of hydrogen atom then
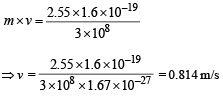
Q.14. A small quantity of solution containing Na24 radio nuclide (half life = 15 hour) of activity 1.0 microcurie is injected into the blood of a person. A sample of the blood of volume 1 cm3 taken after 5 hour show an activity of 296 disintegrations per minute. Determine the total volume of the blood in the body of the person. Assume that radioactive solution mixes uniformly in the blood of the person. (1 curie = 3.7 ×1010 disintegrations per second) (1994 - 6 Marks)
Ans. 5.95 ℓ
Solution. t1/2 = 15 hours
Activity initially A0 = 10–6 Curie (in small quantity of solution of 24Na) = 3.7 × 104dps
Observation of blood of volume 1 cm3
After 5 hours, A = 296 dpm
The initial activity can be found by the formula
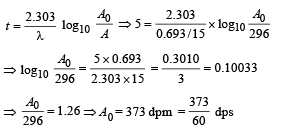
This is the activity level in 1 cm3. Comparing it with the initial activity level of 3.7 × 104 dps we find the volume of blood.
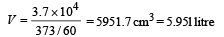
Q.15. A hydrogen like atom (atomic number Z) is in a higher excited state of quantum number n. The excited atom can make a transition to the first excited state by successively emitting two photons of energy 10.2 and 17.0 eV respectively.
Alternately, the atom from the same excited state can make a transition to the second excited state by successively emitting two photons of energies 4.25 eV and 5.95 eV respectively. (1994 - 6 Marks)
Determine the values of n and Z. (Ionization energy of Hatom = 13.6 eV)
Ans. 6, 3
Solution. For hydrogen like atoms
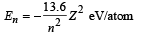
Given En – E2 = 10.2 + 17 = 27.2 eV ..(i)
En – E3 = 4.24 + 5.95 = 10.2 eV
∴ E3 – E2 = 17
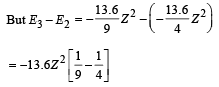
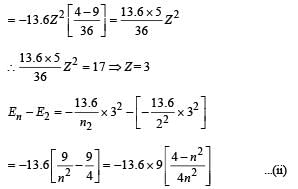
From eq. (i) and (ii),
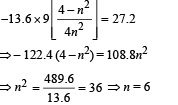
Q.16. An electron, in a hydrogen-like atom, is in an excited state.
It has a total energy of –3.4 eV. Calculate (i) the kinetic energy and (ii) the de Broglie wavelength of the electron. (1996 - 3 Marks)
Ans. (i) 3.4 eV
(ii) 0.66 × 10–9 m
Solution. (i) En = – 3.4 eV
The kinetic energy is equal to the magnitude of total energy in this case.
∴ K.E. = + 3.4 eV
(ii) The de Broglie wavelength of electron
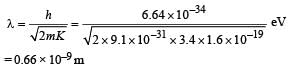
Q.17. At a given instant there are 25% undecayed radio-active nuclei in a sample. After 10 seconds the number of undecayed nuclei reduces to 12.5%. Calculate (i) mean-life of the nuclei, and (ii) the time in which the number of undecayed nuclei will further reduce to 6.25% of the reduced number. (1996 - 3 Marks)
Ans. (i) 14.43 sec.
(ii) 40 sec.
Solution. (i) From the given information, it is clear that half life of the radioactive nuclei is 10 sec (since half the amount is consumed in 10 second. 12.5% is half of 25% pls. note).
Mean life
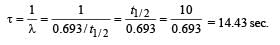
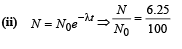
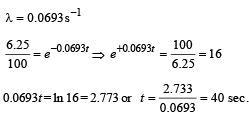
Q.18. Assume that the de Broglie wave associated with an electron can form a standing wave between the atoms arranged in a one dimensional array with nodes at each of the atomic sites. It is found that one such standing wave is formed if the distance d between the atoms of the array is 2Å. A similar standing wave is again formed if d is increased to 2.5 Å but not for any intermediate value of d. Find the energy of the electrons in electron volts and the least value of d for which the standing wave of the type described above can form. (1997 - 5 Marks)
Ans. 151 eV, 0.5 Å
Solution. As nodes are formed at each of the atomic sites, hence

[∵Distance between successive nodes = λ/2]
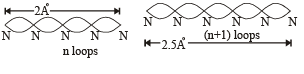
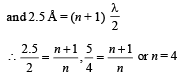
Hence, from equation (1),
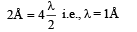
Now, de broglie wavelength is given by
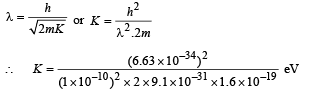
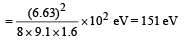
d will be minimum, when
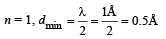
|
446 docs|929 tests
|





















