JEE Advanced (Subjective Type Questions): Ray & Wave Optics- 1 | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. A pin is placed 10 cm in front of a convex lens of focal length 20 cm, made a material of refractive index 1.5. The surface of the lens farther away from the pin is silvered and has a radius of curvature are of 22 cm. Determine the position of the final image. Is the image real as virtual?        (1978)

Ans. 11 cm, Real

Solution. The focal length of the equivalent mirror is

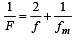
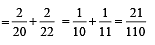
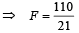
NOTE : Since the focal length is positive it is a converging mirror

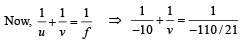
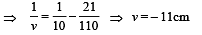
NOTE : The negative sign indicates the image is real.

Q.2. A ray of light is incident at an angle of 60° on one face of prism which has an angle of 30°. The ray emerging out of the prism makes an angle of 30° with the incident ray. Show that the emergent ray is perpendicular to the face through which it emerges and calculate the refractive index of the material of the prism.      (1978)

Ans. 1.732

Solution. The situation can be shown as in the figure.

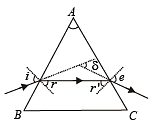
Here, i = 60°,  A = 30°, d = 30°, e = ?

We know that, A + d = i + e ....(1) 

Also, A = r + r' ....(2) 

From (1), e = A + δ – i = 30° + 30° – 60° = 0

As the angle of emergence (e) is 0, hence the emergent ray is normal to the face from which it emerges.

When e = 0, r' = 0 

∴ From (2), A = r = 30°.

From Snell's law, refractive index of prism,

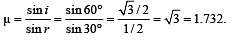
Q.3. A rectangular block of glass is placed on a printed page lying on a horizontal surface. Find the minimum value of the refractive index of glass for which the letters on the page are not visible from any of the vertical faces of the block.       (1979)

Ans. 1.41

Solution. 

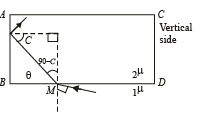
For a grazing incident ray at BD for which i ≈ 90° the angle of refraction (90 – C) is maximum. For this C is least. Let C is greater than the critical angle.

Applying Snell's law at M

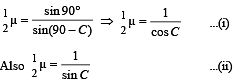
When C is the critical angle.

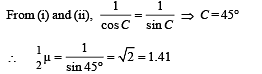
Q.4. What is the relation between the refractive indices μ₁ and μ₂, if the behaviour of light rays is as shown in the figure?       (1979)

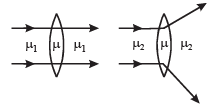
Ans. μ₁ < μ₂

Solution. For case (i), there is no refraction. Therefore  µ₁ = µ 

NOTE : Here the convex lens behaves as a diverging lens.

Therefore, µ < µ₂.

Q.5. An object is placed 21 cm in front of a concave mirror of radius of curvature 10 cm. A glass slab of thickness 3 cm and refractive index 1.5 is then placed close to the mirror in the space between the object and the mirror.

Find the position of the final image formed. (You may take the distance of the near surface of the slab from the mirror to be 1 cm.

Ans. 7.67 cm

Solution. The rays or iginating from A (the point object) suffer refraction before striking the concave mirror.

For the mirror the rays are coming from A'

such that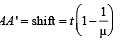

Therefore the object distance

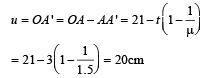
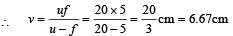
The reflected rays again pass through the glass slab. The image should have formed at B is the absence of glass slab.

But. due to its presence the image is formed at B'.

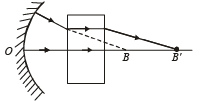
Therefore image distance  = OB + BB'

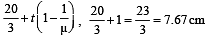
Q.6. The convex surface of a thin concavo-convex lens of glass of refractive index  1.5 has a radius of curvature 20 cm. The concave surface has a radius of curvature 60 cm. The convex side is silvered and placed on a horizontal surface.                   (1981- 6 Marks)

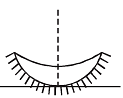
(i) Where should a pin be placed on the optic axis such that its image is formed at the same place? 

(ii) If the concave part is filled with water of refractive index 4/3, find the distance through which the pin should be moved so that the image of the pin again coincides with the pin.

Ans. (i) 15 cm    
(ii)  1.15 cm

Solution. KEY CONCEPT : The given silvered concavo-convex lens behaves like a mirror whose focal length can be calculated by the formula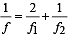

f₁ = focal length of concave surface.
f₂ = focal length of concave mirror

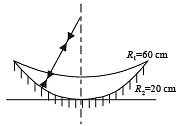
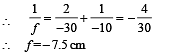
Using mirror formula

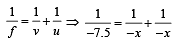
x = 15 cm 

(ii) Let the object distance be u. When water is poured over the concave surface the apparent object distance will be v then

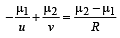
For flat surface  R = ∞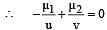

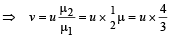
Since the ray enters the lens from water into glass

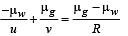
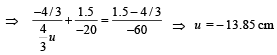
∴ Downward shift  = 15 – 13.85 = 1.15 cm.

Q.7. Screen S is illuminated by two point sources A and B. Another source C sends a parallel  beam of light towards point P on the screen  (see figure). Line AP is normal to the screen and the lines AP, BP and CP are in one plane. The distance AP, BP and CP are 3 m, 1.5 m and 1.5 m respectively. The radiant powers of sources A and B are 90 watts  and 180 watts respectively. The beam from  C is of  intensity 20 watts/m2.

Calculate the intensity at P on the screen.        (1982 - 5 Marks)

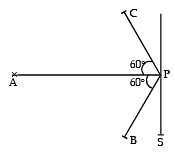
Ans. 13.9

Solution. The total intensity at point P will be = I_A + I_B + I_C

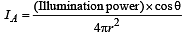
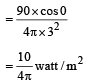
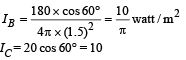
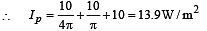
Q.8. A plano convex lens has a thickness of 4 cm . When placed on a horizontal table, with the curved surface in contact with it, the apparent depth of the bottom most point of the lens is found to be 3 cm. If the lens is inverted such that the plane face is in contact with the table, the apparent depth of the centre of the plane face is found to be 25/8 cm. Find the focal length of the lens.         (1984- 6 Marks)

Ans. 75 cm

Solution. Here R = ∝ i.e., plane surface is the refracting surface

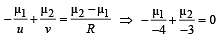
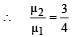     ...(i)

Again applying

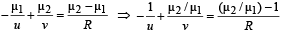
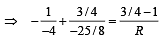
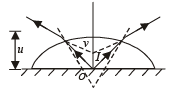
On solving we get R = – 25cm.

Applying Len's maker formula,

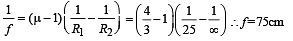
Q.9. A beam of light consisting of two wavelengths, 6500Å and 5200Å, is used obtain interference fringes in a Young’s double slit experiment :       (1985 - 6 Marks) 

(i) Find the distance of the third bright fringe on the screen from the central maximum for wavelength 6500Å.
(ii) What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide?

The distance between the slits is 2 mm and the distance between the plane of the slits and the screen is 120 cm.

Ans. (i) 1.17 × 10^–3 m,
(ii) 1.56 × 10^–3 m

Solution. (i) The distance of the nth bright fringe from the central maxima is given by the expression

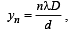For  3rd bright fringe n = 3

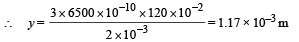
(ii) Let nth bright fringe of wavelength 6500 Å coincide with mth bright fringe of wavelength 5200Å. Their distance will be same from the central bright. Therefore,

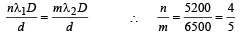
i.e., at the least distance 4th bright fringe of 6500 Å will coincide with 5th bright fringe of 5200 Å.  Its distance from the central maxima will be

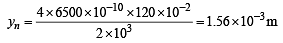
Q.10. Monochromatic light is incident on a plane interface AB between two media of refractive indices n₁ and n₂ (n₂ > n₁) at an angle of incidence q as shown in fig. The angle θ is infinitesimally greater than the critical angle for the two media so that total internal reflection takes place. Now if a transparent slab DEFG of uniform thickness and of refractive index n₃ is introduced on the interface (as shown in the figure), show that for any value of n₃ all light will ultimately be reflected back again into medium II. Consider separately the cases       (1986 - 6 Marks)

(i) n₃ <n ₁ and 
(ii) n₃ >n₁.

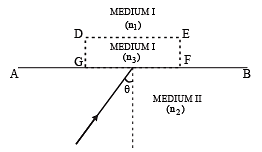
Solution. KEY CONCEPT : For total  internal reflection, the conditions are 

The object should be in the denser medium. 

The angle of incidence should be greater than the critical angle

Case (i) : When n₃ < n₁ 

Obviously n₃ < n₂ and the angle θ is greater than the critical angle required for the ray passing from medium II to medium III. Therefore total internal reflection will also take place when a ray strikes with the same angle at the interface of medium II and medium III.

Case (ii) : n₃ > n₁ but n₃ < n₂ 

The ray will get refracted in medium III as the angle θ will now be less than the critical angle required for medium II and medium III pair.

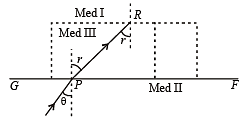
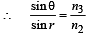 (Applying Snell's law at P)

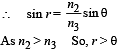
When the refracted ray PR meets the boundary DE, it is travelling from a denser medium to a rarer medium. Therefore the ray will be totally internally reflected at DE if its angle of incidence r is more than the critical angle for med III and I.

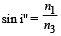
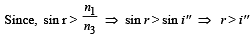
Therefore ray PR will be totally internal reflected along RQ.

On reaching Q, the ray will be refracted in med II. Thus, the ray will ultimately be reflected back in medium II.

Q.11. A right prism is to be made by selecting a proper material and the angles A and B (B < A) , as shown in Figure. It is desired that a ray of light incident on the face AB emerges parallel to the incident direction after two internal reflections.

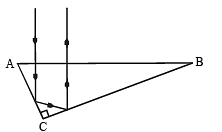
(i) What should be the minimum refractive index n for this to be possible ?

(ii) For n = 5/3 is it possible to achieve this with the angle B equal to 30 degrees ?                      (1987 - 7 Marks)

Ans. (i) √2 (ii)  No

Solution. (i) Let x is the incident angle for reflection at AC. For total internal reflection x > i_C (critical angle)

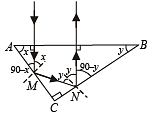
Let y be the incident angle of the ray on face CB. For total internal reflection

internal reflection 

y > i_C 

∴ x + y > 2i_C 

But x = ∠A and y = ∠B (from geometry) 

∴ x + y = 90° 

⇒ 90 > 2iC ⇒ i_C < 45° 

The refractive index of the medium for this to happen.

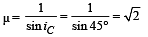
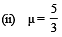
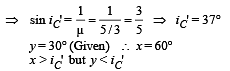
⇒ Total internal reflection will take place on face AC but not on CB.

Q.12. A parallel beam of light travelling in water (refractive index = 4/3) is refracted by a spherical air bubble of radius 2 mm situated in water. Assuming the light rays to be paraxial            (1988 - 6 Marks) 

(i) Find the position of the image due to refraction at the first surface and the position of the final image. 

(ii) Draw a ray diagram showing the positions of both the images.

Ans. (i)  –6 mm, –5 mm

Solution. (i) Initially the object is in denser medium and u = ∞ using the formula of refraction at a spherical surface for AB

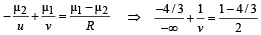
⇒ v = – 6 mm 

NOTE : This is the position of the image due to refraction at the first surface. This image will behave as a virtual object for the refraction at the second surface. 

u = – 6 – 4 = – 10 mm 

Again using the formula of refraction at a spherical surface for CD

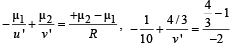
⇒ v' = – 5 mm.

The is the position of final image. 

(ii) Ray Diagram.

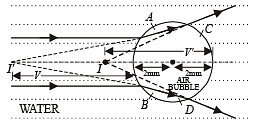
Q.13. In a modified Young’s double slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000 Å and intensity (10/ π) W m^–2 is incident normally on two circular apertures A and B of radii 0.001 m and 0.002 m respectively. A perfectly transparent film of thickness 2000 Å and refractive index 1.5 for the wavelength of 6000 Å is placed in front of aperture A, see fig. Calculate the power (in watts) received at the focal spot F of the lens.

The lens is symmetrically placed with respect to the apertures. Assume that 10% of the power received by each aperture goes in the original direction and is brought to the focal spot.               (1989 - 8 Mark)

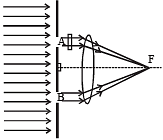
Solution. The power transmitted through A

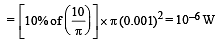
The power transmitted through B

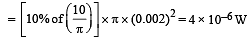
Let Δφ be the phase difference introduced by film

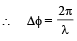 (path difference introduced by the film)

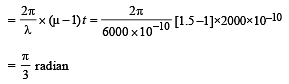
The power received at F

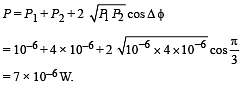
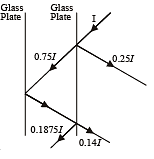
Q.14. A narrow monochromatic beam of  light of intensity I is incident on a glass plate as shown in figure. Another identical glass plate is kept close to the first one and parallel to it. Each glass plate reflects 25 per cent of the light incident on it and transmits the remaining. Find the ratio of the minimum and the maximum intensities in the interference pattern formed by the two beams obtained after one reflection at each plate.                    (1990 - 7 Mark)

Ans. 1/49

Solution. As shown in the figure, the interference will be between 0.25 I = I₁ and 0.14 I = I₂

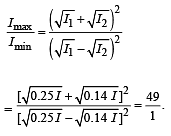
Q.15. Two parallel beams of light P and Q (separation d) containing radiations of wavelengths 4000 Å and 5000 Å (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in fig.  The refractive index of the prism as a function of wavelength is given by the relation.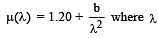 is in Å and b ispositive constant. The value of b is such that the condition for total reflection of the face AC is just satisfied for one wave length and is not satisfied for the other.          (1991 - 2 + 2 + 4  Marks)

(a) Find the value of b. 
(b) Find the deviation of the beams transmitted through the face AC 
(c) A convergent lens is used to bring these transmitted beams into focus. If the intensities of transmission form the face AC, are 41 and I respectively, find the resultant intensity at the focus.

Ans. (a) 0.8 × 10^–14 m² 
(b) 27.2°  
(c)  9I

Solution. (a) λ₁ = 4000 Å and λ₂ = 5000 Å

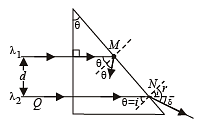
For total internal reflection to take place, q should be greater than C. For smaller values of C, the values of m should be high or in other words the value of l should be small.

Therefore, total internal reflection will be given by 

λ1 = 4000 Å 

Here, sin θ = 0.8 (given) ⇒ θ = 53.1°

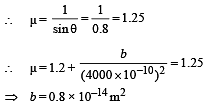
(b) Applying Snell's law at N for wavelength λ₂

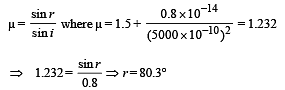
From the figure it is clear that the deviation, 

δ = r – i = 80.3° – 53.1° = 27.2°

(c) The intensities of transmitted beams are 4I and I respectively.

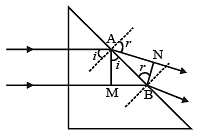
Path diff =  μ(MB)- AN

= 0

Since both the radiations are mutually coherent and while coming to focus these travel equal paths, therefore, these two beams will arrive in phase at focus. 

∴ Resultant Intensity

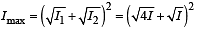
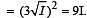
Q.16. Light is incident at an angle α on one planar end of a transparent cylindrical rod of refractive index μ. Determine the least value of μ so that the light entering the rod does not emerge from the curved surface of rod irrespective of the value of μ             (1992 - 8  Marks)

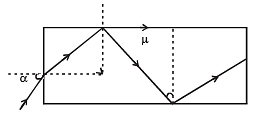
Ans. √2

Solution. The light entering the rod does not emerge from the curved surface of the rod when the angle (90° – β) is greater than the critical angle.

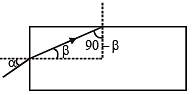
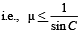 where C is the critical angle.

Here, C = 90 – β

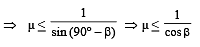
As a limiting case, 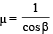     ... (i)

Applying Snell's law at A

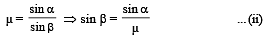
NOTE : The smallest angle of incidence on the curved surface is when α = π/2. This can be taken as a limiting case for angle of incidence on plane surface.

From (ii)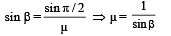
    ... (iii)

From (i) and (ii), sin β = cos β 

⇒ β = 45°

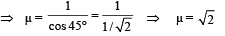
This is the least value of the refractive index of rod for light entering the rod and not leaving it from the curved surface.

Q.17. In Fig., S is a monochromatic point source emitting light of wavelength λ = 500nm. A thin lens of circular shape and focal length 0.10 m is cut into two identical halves L₁ and L₂ by a plane passing through  a diameter. The two halves are placed symmetrically about the central axis SO with a gap of 0.5 mm. The distance along the axis from S to L₁ and L₂ is 0.15 m while that from L₁ and L₂ to O is 1.30 m. The screen at O is normal to SO.                (1993 - 5+1  Marks)

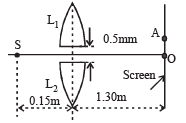
(i) If the third intensity maximum occurs at the point A on the screen, find the distance OA. 
(ii) If the gap between L₁ and L₂  is reduced from its original value of 0.5mm, will the distance OA increase, decrease, or remain the same?

Ans. (i) 10^–3 m  
(ii)  increase

Solution.  (i) In this case, the two identical halves of convex lens will create two seperate images S₁ and S₂ of the source S. These Images (S₁ and S₂) will behave as two coherent sources and the further dealing will be in accordance to Young's double slit experiment.

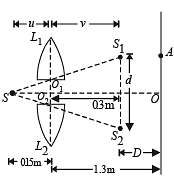
For lens L₁ 

The object is S 

u = – 0.15 m,  v = ?,    f = + 0.1 m

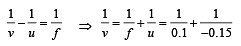
⇒ v =  0.3 m 

Δ SO₁O₂ and Δ SS₁S₂ are similar. Also the placement of O₁ and O₂ are symmetrical to S

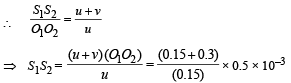
⇒ S₁S₂ = d = 1.5 × 10^–3 m  ∴ D = 1.3 – 0.3 = 1m

The fringe width

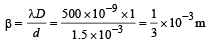
∴ Therefore,

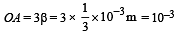
(ii) If the gap between L₁ and L₂ i.e., O₁O₂ is reduced.

Then d will be reduced. Then the fringe width will increase and hence OA will increase.

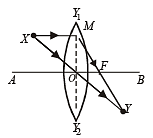
Q.18. An image Y is formed of point object X by a lens whose optic axis is AB as shown in figure. Draw a ray diagram to locate the lens and  its focus. If the image Y of the object X is formed by a concave mirror (Having the same axis as AB) instead of lens, draw another ray diagram to locate the mirror and its focus. Write down the steps of construction of the ray diagrams.     (1994 - 6 Marks)

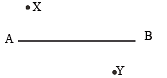
Solution. (i) Since Y is below of optic axis, therefore the image is real and inverted.

(i) STEPS OF CONSTRUCTION OF DIAGRAM.

For convex lens 

(1) Join XY. This represents the ray originating from the source and meeting the image Y. Since the ray is undeviated after passing through the lens, therefore O is the optical centre of the lens. Draw Y₁OY₂ perpendicular to AB. 

(2) Draw a ray from X, parallel to AB. It strikes Y₁OY₂ at M. Join MY. It cuts AB at F. This is the focus of the convex lens.

(ii) For concave mirror 

As the image is real and inverted, the concave mirror has to be placed towards the left of X. To find the exact position of the concave mirror, we draw a line YY' perpendicular to AB such that BY = BY'

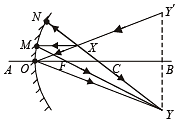
Join Y'X and extend the line to meet AB at O. If the concave mirror is placed at O then after reflection at O, this line will meet Y.

To find the radius of curvature of the mirror 

Join X and Y. Let it cut AB at C. This C should be the centre of curvature of the concave mirror. With OC as radius, draw a part of sphere. This is the concave mirror.

To find the focus of the concave mirror 

Draw XM parallel to the principal axis. Join M to Y. Let it cut AD at F. Therefore, F is the focus of concave  mirror.

Q.19. A ray of light travelling in air is incident at grazing angle (incident angle ≅ 90°) on a long rectangular slab of a transparent medium of thickness t = 1.0 m (see figure below).

The point of incidence is the origin A(0, 0). The medium has a variable index of refraction n(y) given by

n(y) = [ky^3/2+ 1]^1/2, where k = 1.0 (metre) ^-3/2

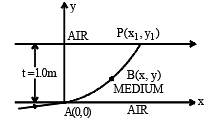
The refractive index of air is 1.0.         (1995 - 10 Marks) 

(a) Obtain a relation between the slope of the trajectory of the ray at a pint B(x, y) in the medium and the incident angle at that point.
(b) Obtain an equation for the trajectory y(x) of the ray in the medium.
(c) Determine the coordinates (x₁ ,y₁) of the point P, where the ray intersects the upper surface of the slabair boundary.
(d) Indicate the path of the ray subsequently. 

Ans.

(c)  (4m, 1m)

Solution. (a) SLOPE AT P 

To find the slope at B, we draw a tangent to the trajectory at B. The trajectory is such that as the ray passes through the rectangular transparent medium, the ray continuously deviates towards the normal. The tangent at B makes an angle θ with the x-axis. Therefore, the slope at point B is tan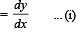

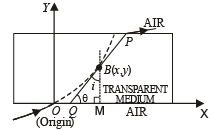
i is the angle of incidence at B then according to ΔBQM

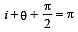        ... (ii)

Substituting the value of q from (ii) in (i)

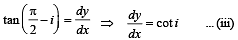
(b) EQUATION OF TRAJECTORY 

According to Snell's law, when light propagates through a series of parallel layers of different media, then n sin i = constant 

Let us consider the rectangular state to be made up of parallel layers such that as we move in the + Y direction, the refractive index increases as given by the relationship

n (y) = [ky^3/2 + 1]^1/2 ...(iv)

Applying Snell's law at O, we get 1 × sin 90° = constant = 1.

Again applying Snell's law at B, we get 

n sin i = const. = 1 (from above equation)

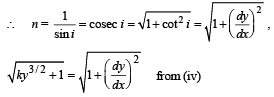
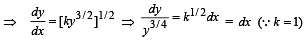
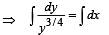
⇒ 4_y^1/4 =  x + C where C is an integration constant.

But at x = 0, y = 0

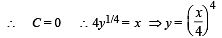
(c) CO-ORDINATES (x₁, y₁) OF THE POINT P 

At P, y = 1m     ∴ x = 4 y^{1 /4} =4 

The coordinates of P are (4m, 1m) 

(d) The refractive index at P

n_p = [ky^3/2 + 1]^1/2 = [1 (1)^3/2 + 1]^1/2 = √2

If i_p is angle of incidence at P then according to Snell's law,

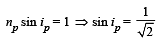
Also by Snell's law, n_air sin r_p = n_p sin i_p

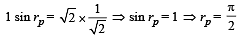
⇒ After emerging from the rectangular glass slab, the light ray becomes parallel to slab length.

Q.20. A right angled prism (45° –90°–45°) of refractive index n has a plate of refractive index n₁(n₁ < n) cemented to its diagonal face. The assembly is in air. A ray is incident on AB.

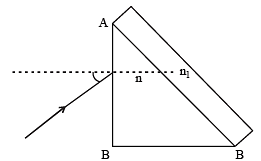
(i) Calculate the angle of incidence at AB for which the ray strikes the diagonal face at the critical angle. 
(ii) Assuming n = 1.352 calculate the angle of incidence at AB for which the refracted ray passes through the diagonal face undeviated.      (1996 - 3 Marks)

Ans.

Solution. (i) The ray incident on AB at M makes an angle of incidence i. It gets refracted at M. The angle of refraction is r. Applying Snell's law at M

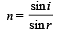               ...(i)

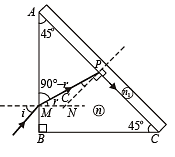
From fig

∠APM = 180° – (45° + 90° – r) = 45° + r and  C = 90° – (45° + r) = 45° – r

The ray after refraction at M enter the prism and strikes its diagonal face AC making an angle C with the normal at P.

Here C is the critical angle, therefore, the ray after refraction at P makes angle of refraction 90° Applying Snell's law at P

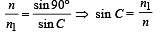       ... (ii)

From (i), sin i = n sin r   = n sin (45° – C)                  

= n [sin 45° cos C – cos 45° sin C]

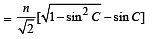
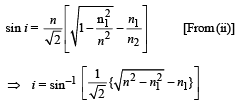
(ii) Angle of incidence at AB for which the refracted ray passes through the diagonal face undeviated. For this to happen, the angle of incidence of ray MP on diagonal face should be zero. It means that the ray should strike normal to AC.

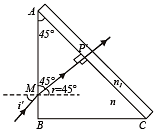
Applying Snell's law at M, we get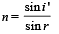

Since ∠AP'M = 90° ∠ AMP = 45 ⇒ r = 45º

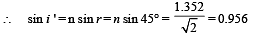
⇒ i ' = 72.94°