JEE Advanced (Subjective Type Questions): Ray & Wave Optics- 2 | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.21. A double-slit apparatus is immersed in a liquid of refractive index 1.33. It has slit separation of 1mm, and distance between the plane of slits and screen is 1.33 m. The slits are illuminated by a parallel beam of light whose wavelength in air is 6300 Å. (1996 - 3 Marks)
(i) Calculate the fringe-width.
(ii) One of the slits of the apparatus is covered by a thin glass sheet of refractive index 1.53. Find the smallest thickness of the sheet to bring the adjacent minimum on the axis.
Ans. (i) 6.3 × 10–4 m (ii) 1.575 × 10–6 m
Solution. 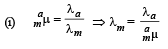
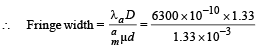
= 6.3 × 10–4m
(ii) KEY CONCEPT : The shift of fringes when one slit is covered with thin glass sheet is
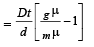
where, t = thickness of glass sheet.
The shift has to be such that the minima shifts to the axis.
For this the shifting of the fringes should be β/2 where b is fringe width
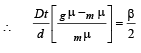
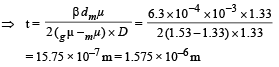
Q.22. A thin plano-convex lens of focal length f is split into two halves: one of the halves is shifted along the optical axis . The separation between object and image planes is 1.8 m.
The magnification of the image formed by one of the halflenses is 2. Find the focal-length of the lens and separation between the two halves. Draw the ray diagram for image formation. (1996 - 5 Marks)
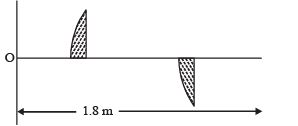
Ans. 0.4m, 0.6m
Solution.
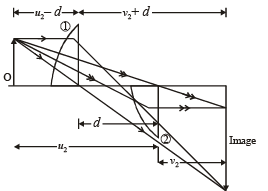
Given u2 + v2 = 1.8 m ... (i)
The magnification of lens (1) is 2

From (i) and (ii)
u2 = 0.6+d , v2 = 1.2 – d
Applying lens formula
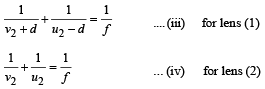
From (iii) and (iv)
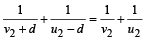
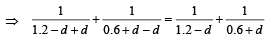
On solving, we get
⇒ d = 0.6 m
Substituting this value in (iv)
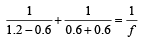
∴ f = 0.4 m
Q.23. In Young’s experiment, the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index 1.7. Interference pattern is observed using light of wavelength 5400 Å. It is found that the point P on the screen where the central maximum (n = 0) fells before the glass plates were inserted now has 3/4 the original intensity. It is further observed that what used to be the fifth maximum earlier, lies below the point P while the sixth minimum lies above P. Calculate the thickness of the glass plate. (Absorption of light by glass plate may be neglected.) (1997 - 5 Marks)
Ans. 9.3 × 10–6m
Solution.
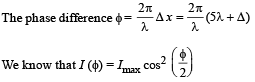
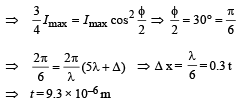
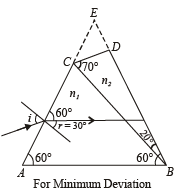
Q.24. A prism of refractive index n1 and another prism of refractive index n2 are stuck together without a gap as shown in Figure.
The angles of the prisms are as shown. n1 and n2 depend on λ, the wavelength of light, according to 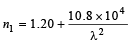 and
and 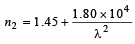 where λ is in nm. (1998 - 8 Marks)
where λ is in nm. (1998 - 8 Marks)
(a) Calculate the wavelength λ0 for which rays incident at any angle on the interface BC pass through without bending at that interface.
(b) For light of wavelength λ0, find the angle of incidence i on the face AC such that the deviation produced by the combination of prisms is minimum.
Ans. (a) 600 nm
Solution.
(a) The rays of wavelength λ0 incident at any angle on the interface BC will pass through without bending, provided the refractive indices n1 and n2 have the same value for the wavelength λ0. Equating the expressions of n1 and n2, we get
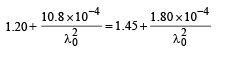
(where λ0 is in nm)
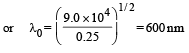
(b) For the wavelength 600 nm, the combination of prism acts as a single prism shaped like an isosceles triangle (ABE). At the minimum deviation, the ray inside the prism will be parallel to the base. Hence, the angle of refraction on the face AC will be r = 30°.
Now sin i = n sin r = n sin 30° = n/2 ... (1)
The value of n at 600 nm is
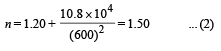
From (1) and (2),
the angle of incidence is 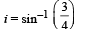
Q.25. A coherent parallel beam of microwaves of wavelength λ = 0.5 mm falls on a Young’s double slit apparatus. The separation between the slits is 1.0 mm. The intensity of microwaves is measured on a screen placed parallel to the plane of the slits at a distance of 1.0 m from it as shown in Fig.
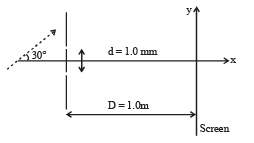
(a) If the incident beam falls normally on the double slit apparatus, find the y-coordinates of all the interference minima on the screen.
(b) If the incident beam makes an angle of 30° with the x axis (as in the dotted arrow shown in Figure), find the y-coordinate of the first minima on either side of the central maximum. (1998 - 8 Marks)
Ans. (a) ± 0.26 m, ±1.13 m
(b) 1.13 m, 0.26 m
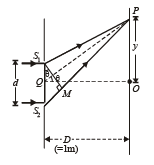
Solution. (a) The path difference (Δx) from the ray starting from S1 and S2 and reaching a point P will be
Δx = d sin θ
We know that the path difference for minimum intensity is
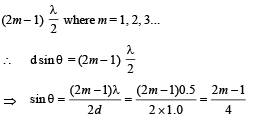
Also -1 < sin θ < 1 . Therefore, possible values of m are ± 1, ± 2, 0
From Δ POQ
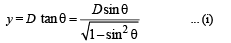
Positions of minima
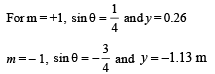
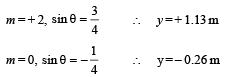
(b) WHEN THE INCIDENT BEAM MAKES AN ANGLE OF 30° WITH X-AXIS
Two cases arise as shown by the following two figures.
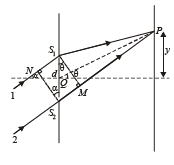
Path difference between ray 1 and 2 reaching P = S2M – NS1
∴ Δx1 = d sin θ - d sinα (Case 1)
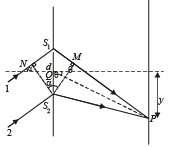
Path difference between ray 1 and 2 reaching P = NS1 + S1M
Δx2 = d sin α + d sin θ (Case 2)
Position of Central maxima : Path difference should be zero. Therefore
Δx1 = 0 or Δx2 = 0
⇒ d sin α = d sin θ

For first minima; 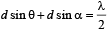
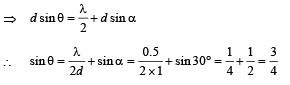
From equation (i), y = 1.15m
For first minima on the other side
Q.26. The Young’s double slit experiment is done in a medium of refractive index 4/3. A light of 600 nm wavelength is falling on the slits having 0.45 mm separation. The lower slit S2 is covered by a thin glass sheet of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in Figure. (1999 - 10 Marks)
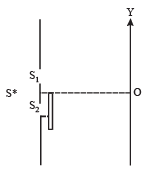
(a) Find the location of the central maximum (bright fringe with zero path difference) on the y – axis.
(b) Find the light inten sity at poin t O relative to th e maximum fringe intensity.
(c) Now, if 600 nm light is replaced by white light of range 400 to 700 nm, find the wavelengths of the light that form maxima exactly at point O.
[All wavelengths in this problem are for the given medium of refractive index 4/3. Ignore dispersion]
Ans. (a) 4.33 × 10–3 m
(b) 0.75
(c) 0.65 × 10–6 m, 0.433 × 10–6 m
Solution. (a) Let the central maxima is obtained at a distance x below O. [This is because a glass sheet is present in front of S2 which increases its path length to the screen.
Therefore the path length of ray from S1 to the screen should also increase].
Here,
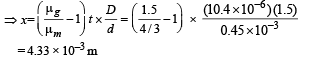
(b) For O, path difference 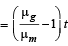
∴ Phase difference
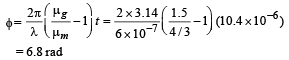
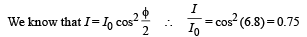
(c) For maximum at O
Again path difference 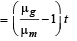
We know that for maxima, path difference = nλ
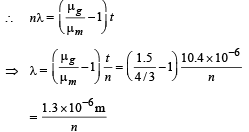
Putting different values of n for find the wave length in the range of 0.4 × 10–6 m to 0.7 × 10–6 m we get λ = 0.65 × 10–6 m and 0.433 × 10–6 m
Q.27. The x – y plane is the boundary between two transparent media. Medium –1 with z > 0 has a refractive index √2 and medium –2 with z < 0 has a refractive index √3 . A ray of light in medium –1 given by the vector 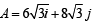 –10 k is incident on the plane of separation. Find the unit vector in the direction of the refracted ray in medium –2. (1999 - 10 Marks)
–10 k is incident on the plane of separation. Find the unit vector in the direction of the refracted ray in medium –2. (1999 - 10 Marks)
Ans.
Solution.
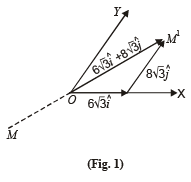
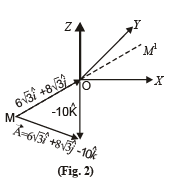
Figure 1 shows vector 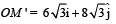
Figure 2 shows vector 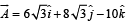
The perpendicular to line MOM' is Z-axis which has a unit vector of 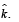
Angle between vector 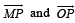 can be found by dot product.
can be found by dot product.
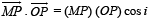
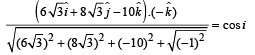
⇒ i = 60°
Unit vector in the direction of MOM' from fig. (1) is
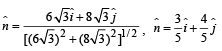
To find the angle of refraction, we use Snell's law
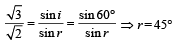
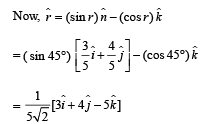
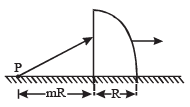
Q.28. A quarter cylinder of radius R and refractive index 1.5 is placed on a table. A point object P is kept at a distance of mR from it. Find the value of m for which a ray from P will emerge parallel to the table as shown in Figure. (1999 - 5 Marks)
Ans. 4/3
Solution. First of all, we consider the refraction at plane surface. Here the image of P will form at I' after refraction from I surface.
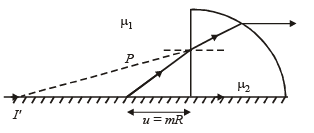
For plane surface :
Object distance u = – mR
Radius of curvature of the plane surface = ∞
The ray is coming from air and incident on the glas.
Here µ1 = 1, µ2 = 1.5.
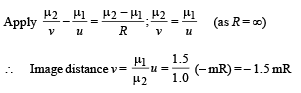
Now we consider refraction at the curved surface.
Object distance, u = – (1.5 mR + R)
Here, µ2 = 1, µ1 = 1.5, Image distance, v = ∞,
Radius of curvature = – R
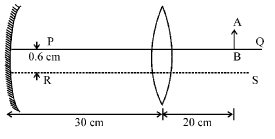
Q.29. A convex lens of focal length 15 cm and a cancave mirror of focal length 30 cm are kept with their optic axes PQ and RS parallel but separated in vertical direction by 0.6 cm as shown. The distance between the lens and mirror is 30 cm. An upright object AB of height 1.2 cm is placed on the optic axis PQ of the lens at a distance of 20 cm from the lens. If A'B' is the image after refraction from the lens and reflection from the mirror, find the distance of A'B' from the pole of the mirror and obtain its magnification. Also locate position of A' and B' with respect to the optic axis RS. (2000 - 6 Marks)
(b) A glass plate of refractive index 1.5 is coated with a thin layer of thickness t and refractive index 1.8. Light of wavelength λ travelling in air is incident normally on the layer. It is partly reflected at the upper and the lower surface of the layer and the two reflected rays interfere. Write the condition for their constructive interference. If l = 648 nm, obtain the least value of t for which the rays interfere constructively. (2000 - 4 Marks)
Ans. (a) 15 cm, 1/2
(b) 90 nm
Solution. (a) For the lens
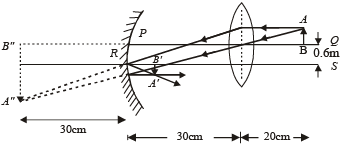
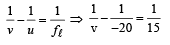
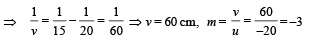
The image is formed to the left of the lens, real, inverted and three times the actual size (3.6 cm in height below PQ).
For the mirror,
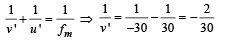
⇒ v' = – 15 cm
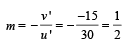
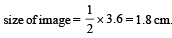
This image will be inverted w.r.t. the original image and its position will be 0.3 cm above RS and 1.5 cm below RS. The position of the image is 15 cm to the right of the mirror.
(b) The path difference between the two rays reflected from the upper surface AB (shown by ray 1, single arrow upwards) and lower surface CD (shown by ray 2 double arrow pointing upwards) is
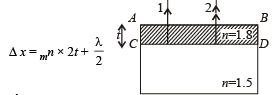
Here λ/2 is the path difference as the ray 1 suffer reflection from a denser medium on surface AB
We known that for constructive interference
Path difference = mλ where m is 1, 2,....
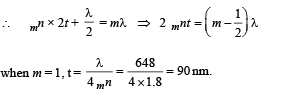
Q.30. The refractive indices of the crown glass for blue and red lights are 1.51 and 1.49 respectively and those of flint glass are 1.77 and 1.73 respectively. An isosceles prism of angle 6o is made of crown glass. A beam of white light is incident at a small angle on this prism. The other flint glass isosceles prism is combined with the crown glass prism such that there is no deviation of the incident light. Determine the angle of the flint glass prism. Calculate the net dispersion of the combined system. (2001 - 5 Marks)
Ans. 4°, – 0.04°
Solution. For no deviation condition
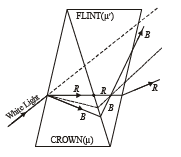
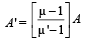
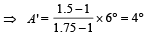
Now, the angular dispersion produced by crown glass prism δb – δr = A (µb – µr)
Also the angular dispersion produced by flint glass prism
δb' – δr' = A' (µb' – µr')
∴ Net deviation in blue light
δb = (μb1 - 1) A1 – (μb2- 1)A2
= (1.51 – 1) 6° – (1.77 – 1) 4° = – 0.02°
Similarly Net deviation of red light
δr = (μr1 - 1) A1 – (μr2- 1)A2
= (1.49 – 1) 6° – (1.73 – 1) 4° = 0.02
∴ Net dispersion = δb – δr = –0.04°
∴ The magnitude of the net angular dispersion = 0.04
Q.31. A vessel ABCD of 10 cm width has two small slits S1 and S2 sealed with identical glass plates of equal thickness. The distance between the slits is 0.8 mm. POQ is the line perpendicular to the plane AB and passing through O, the middle point of S1 and S2. A monochromatic light source is kept at S, 40 cm below P and 2 m from the vessel, to illuminate the slits as shown in the figure below. Calculate the position of the central bright fringe on the other wall CD with respect to the line OQ. Now, a liquid is poured into the vessel and filled upto OQ. The central bright fringe is found to be at Q.
Calculate the refractive index of the liquid. (2001-5 Marks)
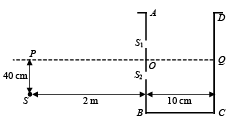
Ans. 2 cm, 1.0016
Solution. (i) O is the middle point of two slits S1 and S2.
S1S2 = d = 0.8 mm
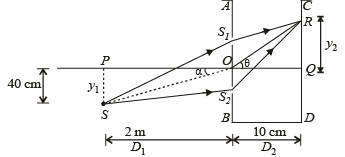
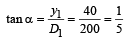
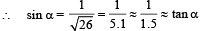
or ΔX1 = d sin α 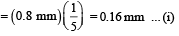
Let R denotes the position of central bright fringe. Net path difference will be zero.
Now ΔX2 = S2 R- S1R or ΔX2 = d sinθ ... (ii)
For central bright fringe
ΔX2 - ΔX1 = 0 or d sin θ - ΔX1 = 0
or = d sin θ = ΔX1 = 0.16 mm
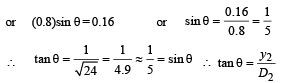
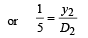
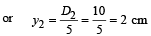
Hence position of central bright fringe is 2 cm above point Q on side CD.
(ii) μ of liquid poured if central fringe is at Q:
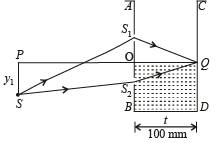
The liquid is poured into vessel upto OQ.
The central bright fringe is formed at Q.
For central bright fringe net path difference = 0.
(μ – 1)t = ΔX1 or(μ – 1)(100) = 0.16
or μ – 1 = 0.0016 or μ = 1.0016
Q.32. A thin biconvex lens of refractive index 3/2 is placed on a horizontal plane mirror as shown in the figure. The space between the lens and the mirror is then filled with water of refractive index 4/3. It is found that when a point object is placed 15 cm above the lens on its principal axis, the object coincides with its own image. On repeating with another liquid, the object and the image again coincide at a distance 25 cm from the lens. Calculate the refractive index of the liquid. (2001-5 Marks)

Ans. 1.6
Solution. The lens maker formula is
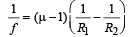
When the space between the lens and the mirror is filled with water, a system of two lenses is formed.
(i) a glass lens
(ii) a plano concave water lens
For glass lens Here R1 = + R and R2 = – R
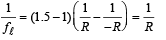
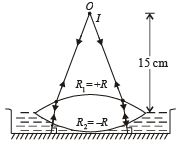
For water lens
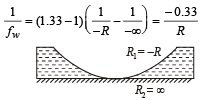
The focal length of the combination of two lenses will be
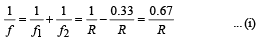
A convex lens placed on a plane mirror behaves like a concave mirror. The image is formed at the object itself if the object is placed at centre of curvature of concave mirror.
After refraction through lens, the rays fall on the plane mirror normally and retrace their path to form image at the object itself.
∴ Focal length of system (f) = 15 cm ... (ii)
From (i) and (ii)
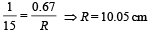
The same situation is repeated with two differences
(a) The object and image distance are now 25 cm and
(b) In place of water there is a new liquid of refraction index µ
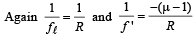
where f ' is the focal
length of new liquid lens.
∴ New combined lens,
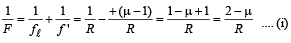
For new combined lens,
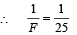 ... (ii)
... (ii)
From (i) and (ii)
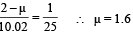
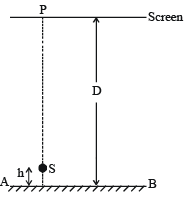
Q.33. A point source S emitting light of wavelength 600 nm is placed at a very small height h above a flat reflecting surface AB (see figure). The intensity of the reflected light is 36% of the incident intensity. Interference fringes are observed on a screen placed parallel to the reflecting surface at a very large distance D from it. (2002 - 5 Marks)
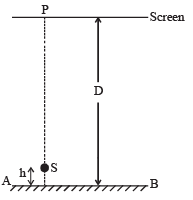
(a) What is the shape of the interference fringes on the screen?
(b) Calculate the ratio of the minimum to the maximum intensities in the interference fringes formed near the point P (shown in the figure).
(c) If the intensity at point P corresponds to a maximum, calculate the minimum distance through which the reflecting surface AB should be shifted so that the intensity at P again becomes maximum.
Ans. (a) circular
(b) 1/16
(c) 300 nm
Solution. (a) Because S is a point source, fringes will be circular.
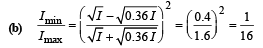
[∵ If intensity of light falling on P directly from S is I, then the intensity of light falling at P after reflection from AB is 0.36 I ]
(c) For maximum at P, path difference = nλ
If AB is shifted by a distance x, it will cause an additional path difference of 2x.
2x = λ (for minimum value of x) ⇒ x = λ/2 = 300 nm
Q.34. Find the focal length of the lens shown in the figure. The radii of curvature of both the surfaces are equal to R. (2003 - 2 Marks)
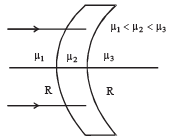
Ans.
Solution. For an object placed at infinity the image after first refraction will be formed at a distance v1
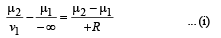
Image afte second refraction will be formed at a distance v2
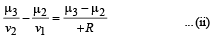
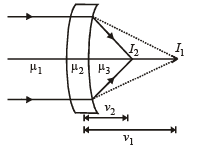
Adding (i) and (ii),
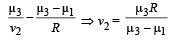
Final image is formed at the focus when incident rays are parallel.
Therefore, focal length will be 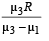
Q.35. Shown in the figure is a prism of angle 30º and refractive index 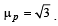 Face AC of the prism is covered with a thin film of refractive index μf = 2.2. A monochromatic light of wavelength λ = 550 nm fall on the face AB at an angle of incidence of 60º. (2003 - 4 Marks)
Face AC of the prism is covered with a thin film of refractive index μf = 2.2. A monochromatic light of wavelength λ = 550 nm fall on the face AB at an angle of incidence of 60º. (2003 - 4 Marks)
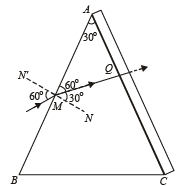
Calculate
(a) angle of emergence.
(b) minimum value of thickness t so that intensity of emergent ray is maximum.
Ans. (a) zero
(b) 125 nm
Solution. (a) Using Snell's law at surface AB
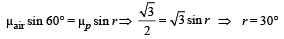
Now, NN' is the normal to surface AB.
∴∠ AMN = 90°
But ∠ QMN = 30° ⇒ ∠AMQ = 60°
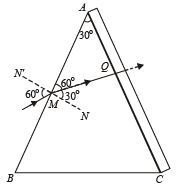
In ΔAMQ
∠ AQM = 180° – (60° + 30°) = 90°
The refracted ray inside the prism hits the other face at 90°; hence deviation produced by this face is zero and hence angle of emergence is zero.
(b) Multiple reflections occur in the film for minimum thickness.
The intensity of emergent ray will be maximum if transmitted waves undergo constructive interference.
∴ For minimum thickness,
⇒ Δx = λ
⇒ Δ x = 2mt = λ,
where t = thickness 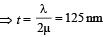
Q.36. A ray is incident on a medium consisting of two boundaries, one plane and other curved as shown in the figure. The plane surface makes an angle 60º with horizontal and curved surface has radius of curvature 0.4 m. The refractive indices of the medium and its environment are shown in the figure.
If after refraction at both the surfaces the ray meets principle axis at P, find OP. (2004 - 2 Marks)
Ans. 6.056 m
Solution. Use Snell's law
n1 sin i = n2 sin r
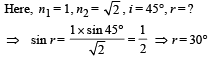
The angle made by refracted ray at B with normal is 30°.
∴ Angle made by the first surface with refracted ray BC is 60°.
Hence the refracted ray at B is parallel to horizontal arrow.
∴ For refraction at spherical surface, u = ∞
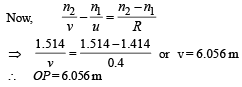
Q.37. In YDSE a light containing two wavelengths 500 nm and 700 nm are used. Find the minimum distance where maxima of two wavelengths coincide. Given D/d = 103, where D is the distance between the slits and the screen and d is the distance between the slits. (2004 - 4 Marks)
Ans. 3.5 mm
Solution. At the place where maxima for both the wavelengths coincide, y will be same for both the maxima, i.e.,
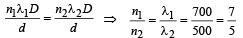
Minimum integral value of n2 is 5.
∴ Minimum distance of maxima of the two wavelengths from central fringe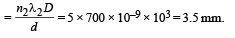
Q.38. An object is moving with velocity 0.01 m/s towards a convex lens of focal length 0.3 m. Find the magnitude of rate of separation of image from the lens when the object is at a distance of 0.4 m from the lens. Also calculate the magnitude of the rate of change of the lateral magnification. (2004 - 4 Marks)
Ans. 0.09 m/sec, 0.35 s–1
Solution. f = 0.3 m, u = – 0.4 m
Using lens formula
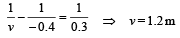
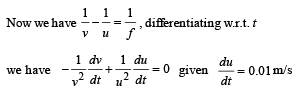
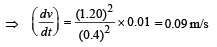
So, rate of separation of the image (w.r.t. the lens) = 0.09 m/s
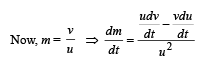
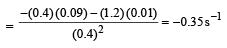
Magnitude of rate of change of lateral magnification = 0.35 s–1.
Q.39. What will be the minimum angle of incidence such that the total internal reflection occurs on both the surfaces? (2005 - 2 Marks)
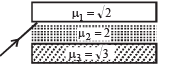
Ans. 60º
Solution. For total internal reflection on interface AB
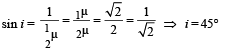
For total internal reflection in interface CD.
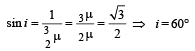
⇒ The minimum angle for total internal reflection for both the interface is 60°.
Q.40. Two identical prisms of refractive index √3 are kept as shown in the figure. A light ray strikes the first prism at face AB. Find, (2005 - 4 Marks)
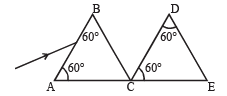
(a) the angle of incidence, so that the emergent ray from the first prism has minimum deviation.
(b) through what angle the prism DCE should be rotated about C so that the final emergent ray also has minimum deviation.
Ans. (a) 60º,
(b) 60º, anticlockwise
Solution. (a) For minimum deviation of emergent ray from the first prism. MN is parallel to AC
∴ ∠BMN = 60°
⇒ ∠r = 30°
Applying Snell's law at M
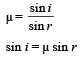
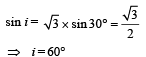
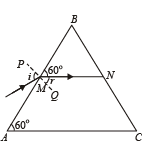
(b) When the prism DCE is rotated about C in anticlockwise direction by 60°, as shown in the figure, then the final emergent ray SR becomes parallel to the incident ray TM. Thus, the angle of deviation becomes zero.
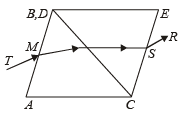
|
446 docs|929 tests
|





















