JEE Advanced (Subjective Type Questions): States of Matter- 1 | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. Calculate density of NH₃ at 30°C and 5 atm pressure. (1978) 

Ans. Sol.  TIPS/Formulae :

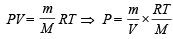
Substituting the value, we get

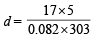= 3.42 g/litre

Q.2. 3.7 g of a gas at 25°C occupied the same volume as 0.184g of hydrogen at 17°C and at the same pressure. What is the molecular weight of the gas? (1979) 

Ans. Sol. Given, moles  = 

mass of gas = 3.7g,

mass of hydrogen = 0.184g T₁ = 298K, T₂ = 17°C = 273 + 17 = 290K
Moles of H₂ = n₁ = 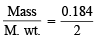 = 0.092

Moles of gas = n₂ =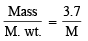 

For hydrogen P₁V₁ = n₁RT₁ .........(i)
For gas P₁V₁ = n₂RT₂ .........(ii)
(∵ Pressure and volume of gas are same)

∴ From equation (i) and equation (ii)

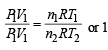
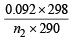
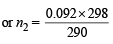
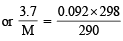
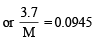
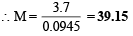
Q.3. A straight glass tube has two inlets X and Y at two ends. The length of tube is 200 cm. HCl gas through inlets X and NH₃ gas through inlet Y are allowed to enter the tube at the same time. What fumes appear at point P inside the tube. Find distance of P from X. (1980) 

Ans. Sol. Let NH₃ diffuse through = x cm

HCl diffuses through = y cm

According to Graham’s law of diffusion

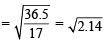= 1.465

x = 1.465 y ... (1)
x + y = 200 cm ... (2)
From these equations; y = 85.2 cm
Distance between P and X = y = 85.2 cm.

Q.4. 1 litre of mixture of CO and CO₂ is taken. The mixture is passed through  a tube containing red hot charcoal. The volume now becomes 1.6 litre. The volumes are measured under the same conditions. Find the composition of mixture by volume. (1980) 

Ans. Sol. Following reaction takes places in tube C + CO₂ —→ 2CO
Volume of mixture of CO and CO₂ = 1L
Let volume of CO₂ in mixture = x
∴ Volume of CO in mixture = 2x
∴ Original volume of CO in mixture = 1 – x
Total volume of CO after reaction = (1 – x) + 2x = 1 + x 1 + x = 1.6
(∵ It is given total volume after reaction = 1.6L)
∴ x = 0.6 L
∴ Volume of CO₂ = 0.6 L Volume of CO = 0.4 L CO₂ : CO = 3 : 2

Q.5. At room temperature, ammonia gas at 1 atm pressure and hydrogen chloride gas at P atm pressure are allowed to effuse through identical pin holes from opposite ends of a glass tube of one metre length and of uniform cross-section.
 Ammonium chloride is first formed at a distance of 60 cm from the end through which HCl gas is sent in. What is the value of P? (1982 - 4 Marks) 

Ans. Sol. Since the pressures of gases are different, and the temperature is constant, the rate at which molecules of the two gases diffuse is directly proportional to the pressure.
This rate of diffusion is also directly proportional to the distance travelled by the gas.

Hence r₁ (of HCl gas) at pressure P = 60 = .....(i)

and r₂ (of NH₃) at 1 atm. pressure P = 40 = 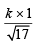 .....(ii)

From (i) and (ii)

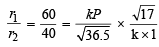
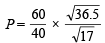= 2.197 atm

Q.6. Calculate the average of kinetic energy, in Joules of the molecules in 8.0 g of methane at 27ºC. (1982 - 2 Marks) 

Ans. Sol. TIPS/Formulae : Total kinetic energy = n (3/2 RT)
where n = Number of moles of the gas
R = Gas constant
T = Absolute temperature Molecular weight of methane, CH₄ = 12 + 4 × 1 = 16
∴  Number of moles of methane in 8.0 gm of methane

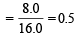
R =  8.314 joules/K/mole, T = 27 + 273 = 300 K
∴ Total kinetic energy of the molecules in 8.0 gm of methane at 27ºC = n × 3/2  RT  = 0.5 × 3/2 × 8.314 × 300 = 1870.65 joules

∴ Average kinetic energy =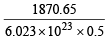

= 6.21 × 10^–21 joules/molecule

Q.7. Oxygen is present in 1 litre flask at a pressure of 7.6 × 10^–10 mm of Hg. Calculate the number of oxygen molecules in the flask at 0ºC. (1983 - 2 Marks) 

Ans. Sol. NOTE THIS STEP :  First we should calculate the number of moles of the gas under the given conditions by the relation PV = nRT

Here P = 7.6 × 10^–10 mm Hg

atm. = 1 × 10^–12 atm.

V = 1 litre, T = 273 + 0 = 273K, R = 0.082 litre atm./K/mol Putting the values in equation

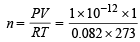moles

Now since 1 mole = 6.023 × 10²³ molecules

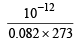moles = 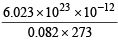molecules

 = 2.7 × 10¹⁰ molecules

Q.8. When 2 gm of a gas A is introduced into an evaluated flask kept at 25ºC, the pressure is found to be one atmosphere. If 3 gm of another gas B is then added to the same flask, the total pressure becomes 1.5 atm. Assuming ideal gas behaviour, calculate the ratio of the molecular weights MA : MB. (1983 - 2 Marks) 

Ans. Sol. From ideal gas equation,

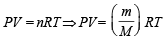
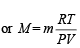
Let the molecular wt. of A and B be M_A and M_B respectively.
Then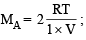  

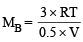
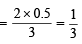
Therefore, the ratio M_A : M_B = 1 : 3

Q.9. Calculate the root mean square velocity of ozone kept in a closed vessel at 20ºC and 82 cm mercury pressure. (1985 - 2 Marks) 

Ans. Sol. 

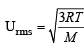
Given T = 20°C = 20 + 273 = 293K R = 8.314 × 10⁷ erg per degree per mol M (of O₃) = 48

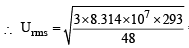= 3.9 × 10⁴ cm sec^–1

Q.10. A spherical balloon of 21 cm diameter is to be filled up with hydrogen at N.T.P. from a cylinder containing the gas at 20 atmospheres at 27ºC. If the cylinder can hold 2.82 litres of water, calculate the number of balloons that can be filled up. (1987 - 5 Marks)

Ans. Sol. Volume of ballon = 4.851 L           (as calculated above)
Let no. of balloons to be filled = n
∴ Total volume occupied by n balloons = 4.851× n
Volume of H₂ present in cylinder = 2.82 L (given)
∴ Total volume of H₂ at NTP = (4.851n + 2.82)L
P₁ = 1 atm                                 P₂ = 20 atm
V₁ = 4.85 × n + 2.82 L               V₂ = 2.82 L
T₁ = 273 K                                 T₂ = 300 K

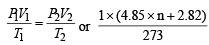
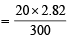
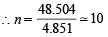
Q. 11. The average velocity at T₁K, and the most probable velocity at T₂K of CO₂ gas is 9.0 × 104 cm sec^–1. Calculate the value of T₁ and T₂. (1990 - 4 Marks) 

Ans. Sol. TIPS/Formulae :

Average velocity =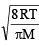

and Most probable velocity =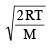

Given -For  CO₂ Average velocity at
T₁ = Most probable velocity at T₂                                        
 = 9 × 10⁴ cm/sec =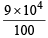m/sec.

  = 9 × 10² m/sec.

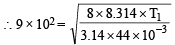...(A)

[Average velocity at T₁K]

and 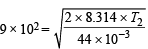 ...(B)

[Most probable velocity at T₂K] On solving,  T₁ = 1682.5 K,   T₂ =  2143.4 K

Q.12. Calculate the volume occupied by 5.0 g of acetylene gas at 50ºC and 740 mm pressure. (1991 - 2 Marks)

Ans. Sol. Applying the general gas equation

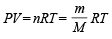
Here, Mol. wt. of acetylene i.e., C₂H₂ (M) = 26, P = 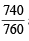 atm,

T = 50°C = 50 + 273 = 323 K

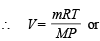
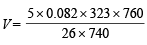= 5.23 L

Q. 13. At 27ºC, hydrogen is leaked through a tiny hole into a vessel for 20 minutes. Another unknown gas at the same temperature and pressure as that of H₂ is leaked through the same hole for 20 minutes. After the effusion of the gases the mixture exerts a pressure of 6 atmosphere. The hydrogen content of the mixture is 0.7 mole. If the volume of the container is 3 litres, what is the molecular weight of the unknown gas? (1992 - 3 Marks) 

Ans. Sol. Using gas equation; PV = nRT

Total no. of moles of gases in the mixture (n)

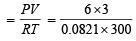= 0.7308 mol.

Thus no. of moles of unknown gas = 0.7308 – 0.7  = 0.0308 mol.
Now we know that

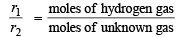
Also we know that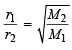 

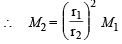
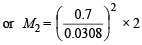  = 1033

Q.14. At room temperature the following reactions proceed nearly to completion : (1992 - 4 Marks) 2NO + O₂ → 2NO₂ → N₂O₄
 The dimer, N₂O₄, solidifies at 262 K. A 250 ml flask and a 100 ml. flask are separated by a stop-cock. At 300 K, the nitric oxide in the larger flask exerts a pressure of 1.053 atm. and the smaller one contains oxygen at 0.789 atm. The gases are mixed by opening the stopcock and after the end of the reaction the flasks are cooled at 220K. Neglecting the vapour pressure of the dimer, find out the pressure and composition of the gas remaining at 220 K. (Assume the gases to behave ideally). 

Ans. Sol. 2NO + O₂ → 2NO₂ → N₂O₄
Calculating the number of moles of NO and O₂ by applying the formula, n =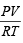

Moles of NO in the larger flask = 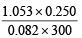 = 0.0107
[250 mL = 0.250  L]

Moles of O₂ in the smaller flask =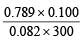 = 0.0032
[100 mL = 0.100  L]

The reaction takes place as follows.

Mols before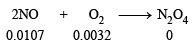  

reaction Mole after         (0.0107 –               0                  0.0032
reaction 2 × .0032)
Hence moles of NO reacting completely with 0.0032 moles of O₂ = 2 × 0.0032 = 0.0064 Moles of NO left = 0.0107 – 0.0064 = 0.0043

NOTE : Oxygen will be completely changed into NO₂ which in turn is completely converted into N₂O₄ which solidifies at 262 K. Hence at 220 K, the dimer is in the solid state and only NO present in excess will remain in the gaseous state occupying volume equal to 350 ml.
Hence pressure (P) of NO gas left

= 0.221 atm

[Total volume = 0.250 + 0.100 = 0.350 L]

Q.15. A gas bulb of 1 litre capacity contains 2.0 × 10²¹ molecules of nitrogen exerting a pressure of 7.57 × 10³ Nm^–2. Calculate the root mean square (r.m.s) speed and the temperature of the gas molecules. If the ratio of the most probable speed  to the root mean square speed is 0.82, calculate the most probable speed for these molecules at this temperature. (1993 - 4 Marks) 

Ans. Sol. Given V= 1L = 10^–3 m³, P = 7.57 × 10^–3 Nm^–2, R = 8.314J, n = 2 × 10²¹/6.023×10²³ moles

PV = nRT or T =

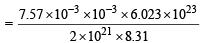= 274.13 K

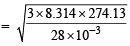 m/s = 494.15 m/s
(Given U)

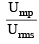= (given)

∴ U_mp = 0.82 × U_rms = 0.82 × 494.15 = 405.2 m/sec

Q.16. A 4 : 1 molar mixture of He and CH₄ is contained in a vessel at 20 bar  pressure . Due to a hole in the vessel, the gas mixture leaks out. What is the composition of the mixture effusing out initially? (1994 - 2 Marks)

Ans. Sol. TIPS/Formulae : Partial pressure = Mole fraction × Total pressure

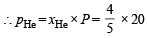= 16 bar

∴ pCH₄ = 20 – 16 = 4 bar

Now applying the formula

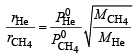
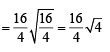
∴ rHe :rCH₃ = 8 :1
∴ Composition of the mixture (He : CH₄) effusing out = 8 :1