JEE Advanced (Subjective Type Questions): Straight Lines & Pair of Straight Lines - 1 | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. A straight line segment of length l moves with its ends on two mutually perpendicular lines. Find the locus of the point which divides the line segment in the ratio 1 : 2. (1978) 

Ans. 

Sol.  Let P (x, y) divides line segment AB in the ratio 1 : 2, so that AP = ℓ /3 and BP = 2ℓ/3 where AB = ℓ .
Then PN = x and PM = y Let ∠ PAM = q = ∠ BPN

In ΔPMA,  

In ΔPNB,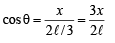 

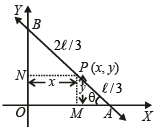
Now,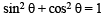 

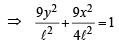⇒ 9x² + 36y² = 4ℓ²

Q.2. The area of a triangle is 5. Two of its vertices are A (2, 1) and B (3, –2). The third vertex C lies on y = x + 3. Find C. (1978)

Ans. 

Sol. As C lies on the line y = x + 3, let the co-ordinates of C be (λ, λ + 3). Also A (2, 1), B (3, – 2).
Then area of ΔABC is given by

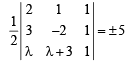
⇒ |2 (– 2 – λ – 3) – 1 (3 – λ) (3λ + 9 + 2λ)| = 10
⇒ | – 2λ – 10 – 3 + λ + 5λ + 9λ = 10
⇒ | 4λ – 4λ = 10
⇒ 4λ – 4 = 10 or4λ – 4 = – 10
⇒ λ = 7/2 or λ = – 3/2

∴ Coordinates of C are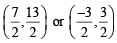 

Q.3. One side of a rectangle lies along the line 4x + 7y + 5 = 0. Two of its vertices are (–3, 1) and (1, 1). Find the equations of the other three sides. (1978) 

Ans. 4x + 7y -11= 0, 7x - 4y -3 = 0 ; 7x - 4y + 25 = 0

Sol. Let side AB of rectangle ABCD lies along 4x + 7y + 5 = 0.
As (– 3, 1) lies on the line, let it be vertex A.
Now (1, 1) is either vertex C or D.

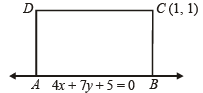
(–3, 1)

If (1, 1) is vertex D then slope of AD = 0 ⇒ AD is not perpendicular to AB.

But it is a contradiction as ABCD is a rectangle.
∴ (1, 1) are the co-ordinates of vertex C.
CD is a line parallel to AB and passing through C, therefore equation of CD is

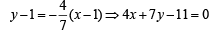
Also BC is a line perpendicular to AB and passing through C, therefore equation of BC is

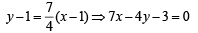
Similarly, AD is a line perpendicular to AB and passing through A (– 3, 1), therefore equation of line AD is

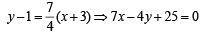
Q.4. (a) Two vertices of a triangle are (5, –1) and (–2, 3). If the orthocentre of the triangle is the origin, find the coordinates of the third point. (b) Find the equation of the line which bisects the obtuse angle between the lines x – 2y + 4 = 0 and 4x – 3y + 2 = 0. (1979)

Ans.

 Sol. (a) AH ⊥ BC ⇒ mAH x mBC =-1

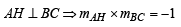
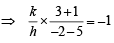
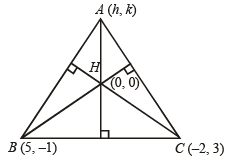
⇒ 4k – 7h = 0 ......... (1)

Also, BH ⊥ AC

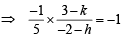    ⇒     3 – k = – 10 – 5h

⇒ 5h – k + 13 = 0 ......... (2)
Solving (1) and (2), we get h = – 4, k = – 7
∴ Third vertex is (– 4, – 7).

(b) The given lines are x – 2y + 4 = 0 .....… (1)
and 4x – 3y + 2 = 0 …..... (2)
Both the lines have constant terms of same sign.
∴ The equation of bisectors of the angles between the given lines are

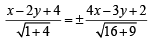
Here a₁a₂ + b₁b₂ > 0 therefore, taking +ve sign on RHS, we get obtuse angle bisector as

.....…(3)

Q.5. A straight line L is perpendicular to the line 5x – y = 1. The area of the triangle formed by the line L and the coordinate axes is 5. Find the equation of the line L. (1980)

Ans. 

Sol.  The given line is 5x – y = 1
∴ The equation of line L which is perpendicular to the given line is x + 5y = l.
This line meets co-ordinate axes at A (l, 0) and B (0, l/5).

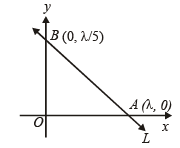
∴ Area of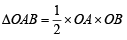  

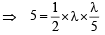
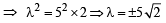
∴ The equation of line L is x + 5y –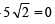  

or x + 5y +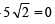

Q.6. The end A, B of a straight line segment of constant length c slide upon the fixed rectangular axes OX, OY respectively. If the rectangle OAPB be completed, then show that the locus of the foot of the perpendicular drawn from P to AB is

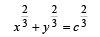 (1983 - 2 Marks)

Ans. 

Sol. From figure,     

x = OA – AL
= c cosα – AN cosα
= c cosα – (AP sin a.) cosα
= c cosα – c sinα .                  
 sinα cosα
= c cosα (1 – sin2α)
= c cos3α

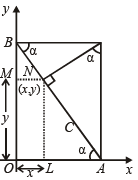
y = OB – MB 

= c sinα – BN sinα
= c sinα – BP cosα sinα
= c sinα – c cosα . cosα sinα
= c sinα (1 – cos2α)
= c sin3α

∴  Locus of (x, y) is 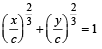or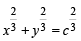

Q.7. The vertices of a triangle are [ at₁t₂, a(t₁ + t₂)], [at₂t₃, a(t₂ + t₃)], [at₃t₁, a(t₃ + t₁) ]. Find the orthocentre of the triangle. (1983 - 3 Marks) 

Ans. Sol. 

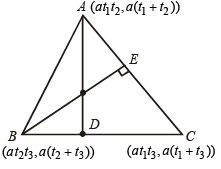
Slope of BC =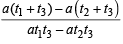

∴ Slope of AD = – t₃ 

∴ Eq. of AD,

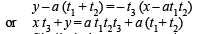....… (1)

Similarly, by symm. equation of BE is

⇒ xt₁ + y = at₁t₂t₃ + a (t₂ + t₃) ….... (2)
Solving (1) and (2),
we get  x = – ay = a (t₁+ t₂ + t₃) + at₁t₂t₃)
∴ Orthocentre H (–a, a (t₁ + t₂ + t₃) + at₁t₂t₃)

Q.8. The coordinates of A, B, C are (6, 3), (–3, 5), (4, – 2) respectively, and P is any point (x, y). Show that the ratio of the area of the triangles ΔPBC and ΔABC is 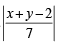          (1983 - 2 Marks) 

Ans. Sol. Area of ΔABC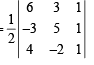  

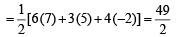
Area of ΔPBC =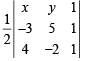

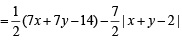
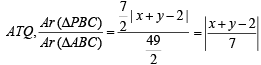
Q.9. Two equal sides of an isosceles triangle are given by the equations 7x -y + 3=0 and x +y - 3=0 and its third side passes through the point (1, –10). Determine the equation of the third side.           (1984 - 4 Marks) 

Ans. Sol. Let equations of equal sides AB and AC of isosceles ΔABC are
7x – y + 3 = 0 .....… (1)
and x + y – 3 = 0 .....… (2)
The third side BC of Δ passes through the point (1, – 10). Let its slope be m.

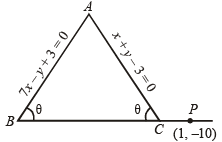
As AB = AC
∴∠B = ∠C
⇒ tan B = tan C .....… (3)
Now slope of AB = 7 and slope of AC = – 1

Using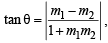 we get

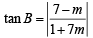and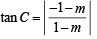 

From eq. (3), we get

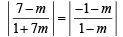
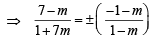
Taking '+ ' sign, we get (7 – m) (1 – m) = – (1+ m) (1 + 7m)
⇒ 7 – 8m + m² + 7m² + 8m + 1 = 0 ⇒ 8m² + 8 = 0  
⇒ m² + 1 = 0
It has no real solution.

Taking '–' sign, we get (7 – m) (1 – m) = (1 + m) (1 + 7m)
⇒ 7 – 8m + m² – 7m² – 8m – 1 = 0
⇒ – 6m² – 16m + 6 = 0  
⇒ 3m² + 8m – 3 = 0
⇒ (3m – 1) (m + 3) = 0  
⇒ m = 1/3, – 3
∴ The required line is

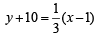or   y + 10 = – 3 (x – 1)

i.e. x – 3y – 31 = 0   or 3x + y + 7 = 0.

Q.10. One of the diameters of the circle circum scribing the rectangle ABCD is 4 y = x + 7 . If A and B are the points (–3, 4) and (5, 4) respectively, then find the area of rectangle. (1985 - 3 Marks) 

Ans. 32 sq. units

Sol. Let O be the centre of the circle. M is the mid point of AB.
Then

OM ⊥ AB
Let OM when produced meets the circle at P and Q.

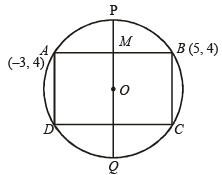
∴ PQ is a diameter perpendicular to AB and passing through M.

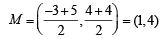
Slope of AB  =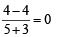 

∴ PQ, being perpendicular to AB, is a line parallel to yaxis passing through (1, 4).
∴ Its equation is x = 1
....… (1)
Also eq. of one of the diameter given is 4y = x + 7 ....… (2)
Solving (1) and (2), we get co-ordinates of centre OO( 1, 2)
Also let co-ordinates of D be (α, b)
Then O is mid point of BD, therefore

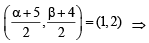  a = – 3, b = 0

∴ D (– 3, 0)
Using the distance formula we get

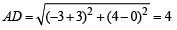
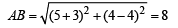
∴ Area of rectangle ABCD = AB × AD = 8 × 4    = 32 square units.

Q.11. Two sides of a rh ombus ABCD ar e par allel to the lines y = x + 2 an d y = 7 x + 3 . If th e diagonals of the rhombus intersect at the point (1, 2) and the vertex A is on the y-axis, fin d possible co-ordinates of A. (1985 - 5 Marks) 

Ans. (0, 0) or (0, 5/2)

Sol. A being on y-axis, may be chosen as (0, a).
The diagonals intersect at P (1, 2).

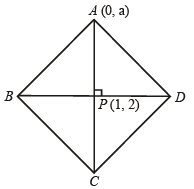
Again we know that diagonals will be parallel to the angle bisectors of the two sides  y = x + 2 and y = 7x + 3

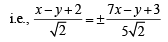
⇒ 5x – 5y + 10 = ± (7x – y + 3)
⇒ 2x + 4y – 7 = 0 and 12x – 6y + 13 = 0
m₁ = – 1/2
m₂ = 2
Let diagonal d₁ be parallel to 2x + 4y – 7 = 0 and diagonal d₂ be parallel to 12x – 6y + 13 = 0.
The vertex A could be on any of the two diagonals. Hence slope of AP is either – 1/2 or 2.

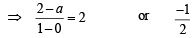
⇒ a = 0             or 5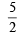 

∴ A is (0, 0) or (0, 5/2)

Q.12. Lines L₁ ≡ ax + by +c= 0 and L₂ ≡ Ix + my + n = 0 intersect at the point P and make an angle θ with each other. Find the equation of a line L different from L₂ which passes through P and makes the same angle θ with L₁. (1988 - 5 Marks) 

Ans.  (a² + b² )(lx + my + n) - 2(al + bm)(ax + by + c) = 0

Sol. Let the equation of other line L, which passes through the point of intersection P of lines L₁ ≡ ax + by + c = 0 .....… (1)
and L₂ ≡ ℓx + my + n = 0 ..…... (2)
be L₁ + λL₂ = 0 i.e.(ax + by + c) + λ(ℓx + my + n) = 0 .....… (3)

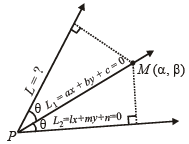
From figure it is clear that L₁ is the bisector of the angle between the lines given by (2) and (3) [i.e. L₂ and L] Let M (α, β) be any point on L₁ then aα + bβ + c = 0  …... (4)
Also from M, lengths of perpendiculars to lines L and L₂ given by equations (3) and (4), are equal

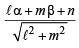
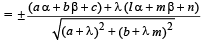
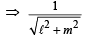
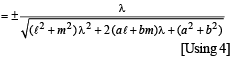
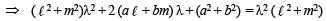
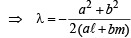
Substituting this value of l in eq. (3), we get L as

(ax + by + c)  (ℓx + my + n) = 0

⇒ (a² + b²)(ℓx + my + n) – 2 (aℓ + bm)(ax + by + c) = 0

Q.13. Let ABC be a triangle with AB = AC. If D is the midpoint of BC, E is the foot of the perpendicular drawn from D to AC and F the mid-point of DE, prove that AF is perpendicular to BE. (1989 - 5 Marks) 

Ans. Sol. Let BC be taken as x-axis with origin at D, the mid-point of BC, and DA will be y-axis.

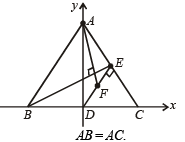
Let BC = 2a, then the co-ordinates of B and C are (– a, 0) and (a, 0).
Let DA = h, so that co-ordinates of A are (0, h).

Then equation of AC is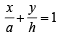....… (1)
And equation of DE ⊥ to AC and passing through origin is

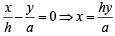.....… (2)
Solving (1) and (2) we get the co-ordinates of pt E as follows

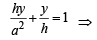h2 y + a2 y = a2 h

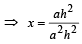
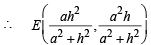
Since F is mid pt. of DE, therefore, its co-ordinates are

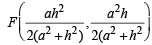
∴ Slope of AF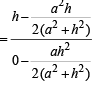 

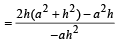
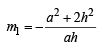⇒.....… (i)

And slope of BE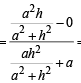 

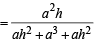
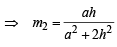....… (ii)

From (i) and (ii), we observe that m₁m₂ = – 1 ⇒ AF ⊥ BE. Hence Proved.

Q.14. Straight lines 3x + 4y = 5 and 4x – 3y = 15 intersect at the point A. Points B and C are chosen on these two lines such that AB = AC. Determine the possible equations of the line BC passing through the point (1, 2). (1990 -  4 Marks) 

Ans. Sol. The given st. lines are 3x + 4y = 5 and 4x – 3y = 15.
Clearly these st. lines are perpendicular to each other (m₁ m₂ = – 1), and intersect at A.
Now B and C are pts on these lines such that  AB = AC and BC passes through (1, 2) From fig. it is clear that ∠B = ∠C = 45°

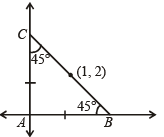
Let slope of BC be m. Then using

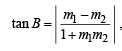we get tan 45°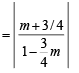

⇒ 4m + 3 = ± (4 – 3m)
⇒ 4m + 3 = 4 – 3m   or   4m + 3 = – 4 + 3m
⇒ m = 1/7 or m = – 7

∴ Eq. of BC is,  

or y – 2 = – 7 (x – 1)
⇒ 7y – 14 = x – 1 or y – 2 = – 7x + 7
⇒ x – 7y + 13 = 0 or 7x + y – 9 = 0