JEE Advanced (Subjective Type Questions): Straight Lines & Pair of Straight Lines - 2 | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.15. A line cuts the x-axis at A (7, 0) and the y-axis at B(0, – 5). A variable line PQ is drawn perpendicular to AB cutting the xaxis in P and the y-axis in Q. If AQ and BP intersect at R, find the locus of R. (1990 -  4 Marks) 

Ans. x² + y² - 7x + 5y = 0

Sol. Eq. of the line AB is

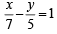     [A (7, 0), B(0, – 5)]

⇒ 5x – 7y – 35 = 0 Eq. of line PQ ⊥ AB is 7x + 5y + l = 0 which meets axes of x and y at pts P(– l/7, 0) and Q (0, – l/5) resp.

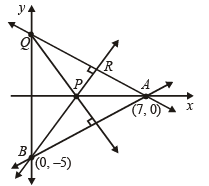
Eq. of AQ is,

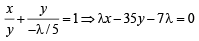........ (2)

Eq. of BP is,

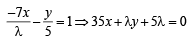......... (3)

Locus of R the pt. of intersection of (2) and (3) can be obtained by eliminating l from these eq. ' s, as follows

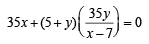
⇒ 35x (x – 7) + 35y (5 + y) = 0  ⇒ x² + y² – 7x + 5y = 0

Q.16. Find the equation of the line passing through the point (2, 3) and making intercept of length 2 units between the lines y + 2x = 3 and y + 2x = 5. (1991 -  4 Marks)

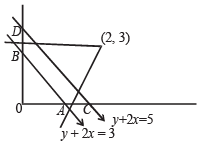
Ans.  3x + 4y -18 = 0 or x - 2 = 0

Sol. Let the equation of line through A which makes an intercept of 2 units between.
2x + y = 3 .......... (1)
and 2x + y = 5 .......... (2)

be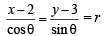

Let AP = r then AQ = r + 2

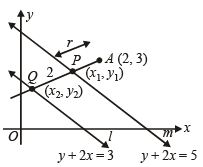
Then for pt P (x₁, y₁),

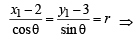
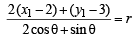
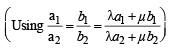
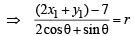
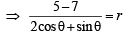
[Using 2x₁ + y₁ = 5 as P (x₁, y₁) lies on 2x + y = 5]

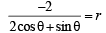 … (i)
For pt Q (x₂, y₂),

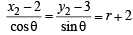
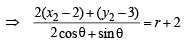
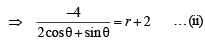
(ii) – (i)

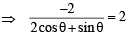
⇒ 2 cosθ + sinθ= – 1 … (3)
⇒ 2 cosθ = – (1 + sinθ)
Squaring on both sides, we get
⇒ 4 cos²θ = 1 + 2 sinθ + sin²θ
⇒ (5 sinθ – 3) (sinθ + 1) = 0
⇒ sinθ = 3/5, – 1
⇒ cosθ = – 4/5, 0 [Using eq. (3)]

∴ The required equation is either

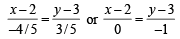
⇒ either 3x – 6 = – 4y + 12 or x – 2 = 0
⇒ either 3x + 4y – 18 = 0 or x – 2 = 0
 

Q.17. Show that all chords of the curve 3 x² -y² – 2x + 4y = 0, which subtend a right angle at the origin, pass through a fixed point. Find the coordinates of the point. (1991 -  4 Marks)

Ans. (1, –2)

Sol. The given curve is 3x² – y² – 2x + 4y = 0 … (1)
Let y = mx + c be the chord of curve (1) which subtends an ∠ of  90° at origin.
Then  the combined eq. of lines joining points of intersection of curve (1) and chord y = mx + c to the origin, can be obtained by making the eq. of curve homogeneous with the help of eq. of chord, as follows.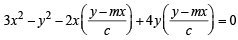

⇒ (3c + 2m) x² – 2 (1+ 2m) xy + (4 – c) y² = 0
As the lines represented by this pair are perpendicular to each other, therefore we must have coeff. of x² + coeff. of y² = 0
⇒ 3c + 2m + 4 – c = 0 ⇒ – 2 = m . 1 + c
Which on comparision with eq. of chord, implies that y = mx + c passes though (1, – 2).
Hence the family of chords must pass through (1, – 2).

Q.18. Determine all values of a for which the point (α, α²) lies inside the triangle formed by the lines 2x + 3y – 1 = 0 (1992 -  6 Marks)
 x + 2y – 3 = 0
 5x – 6y – 1 = 0 

Ans. 

Sol. The points of intersection of given lines are

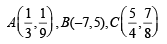
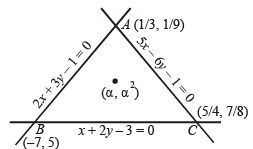
If (α, α²) lies inside the Δ formed by the given lines, then

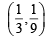and (α, α²) lie on the same side of the line x + 2y – 3
= 0

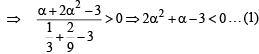
Similarly 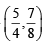and (α, α²) lie on the same side of the line
2x + 3y – 1 = 0.

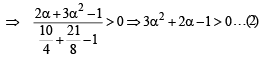
(– 7, 5) and (α, α²) lie on the same side of the line 5x – 6y –1 = 0.

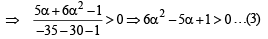
Now common solution of (1), (2) and (3) can be obtained as in the previous method,

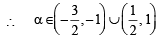
Q.19. Tagent at a point P₁ {other than (0, 0)} on the curve y = x³ meets the curve again at P₂. The tangent at P₂ meets the curve at P₃, and so on. Show that the abscissae of P₁ , P₂ , P₃ ...........P_n , form a G.P. Also find the ratio. [area ( DP₁ , P₂ , P₃ )] /[area ( P₂ P₃ ,P₄ )] (1993 -  5 Marks) 

Ans. 

Sol. The given curve is

y = x³       … (1)
Let the pt, P₁ be (t, t³), t ≠ 0

Then slope of tangent at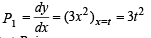 

∴ Equation of tangent at P₁ is y – t³ = 3t² (x – t)
⇒ y = 3t² x – 2t³ ⇒ 3t²x – y – 2t³ = 0 … (2)
Now this tangent meets the curve again at P₂ which can be obtained by solving (1) and (2) i.e., 3t²x – x² – 2t³ = 0
or x³ – 3t²x + 2t³ = 0 (x – t)² (x + 2t) = 0  
⇒ x = – 2t as x = t is for P₁ 
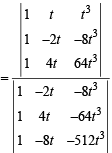
∴ y = – 8t³ Hence pt P₂ is (– 2t, – 8t²) = (t₁ ,t₁³)s ay..
Similarly, we can find that tangent at P₂ which meets the curve again at P₃ (2t₁ , -8t₁³) i.e., (4t, 64t³).
Similarly, P₄ ≡ (-8t ,-512t³) and so on.
We observe that abscissae of pts. P₁, P₂, P₃… are t, – 2t, 4t, … which form a GP with common ratio – 2.
Also ordinates of these pts. t³, – 8t³, 64t³, … also form a GP with common ratio – 8.

Now, 

Now,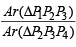 

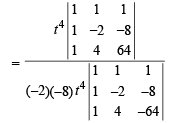
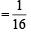  sq. units.

Q.20. A line through A (–5, –4) meets the line x + 3y + 2 = 0, 2x + y + 4 = 0 and x – y – 5 = 0 at the points B, C and D respectively. If (15/AB)² + (10/AC)² = (6/ AD)², find the equation of the line. (1993 -  5 Marks) 

Ans.  2x + 3y + 22 = 0

Sol. Let θ be the inclination of line through A (– 5, – 4). Therefore equation of this line is

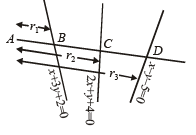
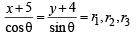
⇒ B (r₁ cosθ– 5, r₁ sinθ – 4)
C (r₂ cosθ – 5, r₂ sinθ – 4)
D (r₃ cosθ – 5, r₃ sinθ – 4)
But B lies on x + 3y + 2 = 0. therefore r₁  cosθ – 5 + 3r₁ sin θ – 12 + 2 = 0

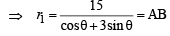
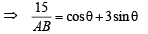… (1)

As C lies on 2x + y + 4 = 0, therefore 2 (r₂ cosθ – 5) + (r₂ sinθ – 4) + 4 = 0

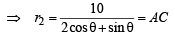
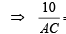= 2cosθ + sinθ … (2)

Similarly D lines on x – y – 5 = 0, therefore r₃ cosθ – 5 – r₃ sinθ + 4 – 5 = 0

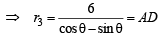
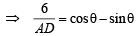… (3)

Now, ATQ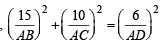

⇒ (cosθ + 3 sinθ)² + (2 cosθ + sinθ)² =  (cosθ – sinθ)² [Using (1), (2) and (3)]
⇒ 4 cos²θ + 9 sin²θ + 12 sinθ cosθ = 0
⇒ 2 cosθ + 3 sinθ = 0

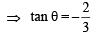
∴ Equation of req. line is  y + 4 =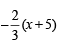  

⇒  2x + 3y + 22 = 0

Q.21. A rectangle PQRS has its side PQ parallel to the line y = mx and vertices P, Q and S on the lines y = a, x = b and x = –b, respectively. Find the locus of the vertex R. (1996 - 2 Marks) 

Ans. x(m² -1) - ym+ (m² +1)b + am = 0

Sol. Let the co-ordinates of Q be (b, a) and that of S be  (– b, b).
Let PR and SQ intersect each other at G.
∵ G is the mid pt of SQ. (∵ diagonals of a rectangle bisect each other)
∴ x co-ordinates of G must be a.
Let the co-ordinates of R be (h, k).
∴ The x-coordinates of P is – h (∵ G is the mid point of PR)
As P lies on y = a, therefore cordinates of P are (– h, a).

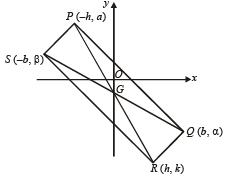
∵ PQ is parallel to y = mx, Slope of PQ = m

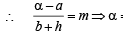 = a + m (b+h)… (1)

Also RQ ⊥ PQ⇒

Slope of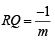 

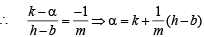… (2)

From (1) and (2) we ge

a + m (b + h)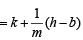 

⇒ (m² – 1) h – mk + b (m² + 1) + am = 0
∴ Locus of vertex R (h, k ) is (m² – 1) x – my + b (m² + 1) + am = 0.

Q.22. Using co-ordinate geometry, prove that the three altitudes of any triangle are concurrent. (1998 - 8 Marks) 

Ans. 

Sol. Let A (x₁, y₁), B (x₂, y₂), C (x₃, y₃) be the vertices of ΔABC

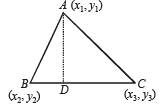
Then equation of alt. AD is

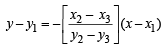
or(x – x₁) (x₂ – x₃) + (y – y₁) (y₂ – y₃) = 0  … (1)
Similarly equations of other two attitudes are
(x – x₂) (x₃ – x₁) + (y – y2) (y₃ – y₁) = 0  …(2)
and (x – x₃) (x₁ – x₂) + (y – y₃) (y₁ – y₂) = 0   …(3)
Now, above three lines will be concurrent if

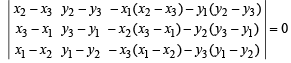
On L.H.S.
Operating R₁ + R₂ + R₃, R₁ becomes row of zeros.
∴ Value of determinant = 0 = R.H.S.
Hence the altitudes are concurrent.

Q.23. For points P = (x 1, y 1) an d Q = (x₂, y₂) of the co-ordinate plane, a new distance d(P, Q) is defined by d(P, Q) = |x₁ – x₂| + |y₁ – y₂|. Let O = (0, 0) and A = (3, 2). Prove that the set of points in the first quadrant which are equidistant (with respect to the new distance) from O and A consists of the union of a line segment of finite length and an infinite ray. Sketch this set in a labelled diagram. (2000 - 10 Marks) 

Ans. 

Sol. Let P = (h, k) be a general point in the first quadrant such that  d (P, A) = d (P, O)
⇒ | h – 3 | + | k – 2 | = | h | + | k | = h + k … (1)
[h and k are + ve, pt (h, k) being in I quadrant.]

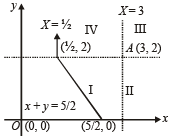
If h < 3, k < 2 then (h, k) lies in region I.
It h > 3, k < 2, (h, k) lies in region II.
If h > 3, k > 2 (h, k) lies in region III.

If h < 3, k > 2 (h, k) lies in region IV.
In region I, eq. (1)

⇒ 3 – h + 2 – k = h + k ⇒ h + k =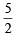 

In region II, eq. (1) becomes

⇒ h – 3 + 2 – k = h + k ⇒ k = 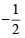not possible.

In region III, eq. (1) becomes
⇒ h – 3 + k – 2 = h + k ⇒ – 5 = 0 not possible.
In region IV, eq. (1) becomes
⇒ 3 – h + k – 2 = h + k ⇒ h = 1/2
⇒ Hence required set consists of line segment x + y = 5/2 of finite length as shown in the first region and the ray x = 1/2 in the fourth region.

Q.24. Let ABC and PQR be any two triangles in the same plane.
 Assume that the prependiculars from the points A, B, C to the sides QR, RP, PQ respectively are concurrent. Using vector methods or otherwise, prove that the prependiculars from P, Q, R to BC, CA, AB respectively are also concurrent. (2000 - 10 Marks) 

Ans. 

Sol. Let the co-ordinates of the vertices of the ΔABC be A (a₁, b₁), B(a₂, b₂) and C (a₃, b₃) and co-ordinates of the vertices of the ΔPQR be P (x₁, y₁), B (x₂, y₂) and R (x₃, y₃)

Slope of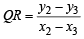  

⇒ Slope of straight line perpendicular to

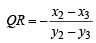
Equation of straight line passing through A (a₁, b₁) and perpendicular  to QR is

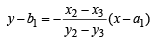
⇒ (x₂ – x₃)x + (y₂ – y₃) y – a₁ (x₂ – x₃) – b₁ (y₂ – y₃) = 0 … (1)

Similarly equation of straight line from B and perpendicular to RP is (x₃ – x₁) x + (y₃ – y₁) y – a₂ (x₃ – x₁) – b₂ (y₃ – y₁) = 0   … (2)
and eqn of  straight line from C and perpendicular to PQ is (x₁ – x₂) x + (y₁ – y₂) y – a₃ (x₁ – x₂) – b₃ (y₁ – y₂) = 0   … (3)
As straight lines (1), (2) and (3) are given to be concurrent, we should have

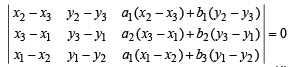… (4)

Operating R₁ → R₁ + R₂+R₃ , we get

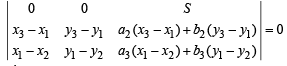
where

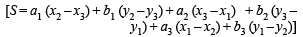
Expanding along R₁ 

⇒ [(x₃ – x₁) (y₁ – y₂) – (x₁ – x₂) (y₃ – y₁) ] S = 0

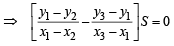
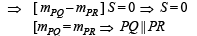
which is not possible in ΔPQR]

⇒ a₁ (x₂ – x₃) + b₁ (y₂ – y₃) + a₂ (x₃ – x₁) + b₂ (y₃ – y₁) + a₃ (x₁ – x₂) + b₃ (y₁ – y₂) = 0 … (5)
⇒ x₁ (a₃ – a₂) + y₁ (b₃ – b₂) + x₂ (a₁ – a₃) + y₂ (b₁ – b₃) + x₃ (a₂ – a₁) + y₃ (b₂ – b₁) = 0    ...(6)
(Rearranging the equation (5)) But above condition shows

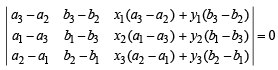 ...(7)

[Using the fact that as (4) ⇔ (5) in the same way (6) ⇔ (7)]
Clearly equation (7) shows that lines through P and perpendicular to BC, through Q and perpendicular to AB are concurrent. Hence Proved.

Q.25. Let a, b, c be real numbers with a² + b² + c² = 1. Show that

the equation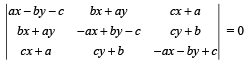  

represents a straight line. (2001 - 6 Marks)

Ans.

 Sol.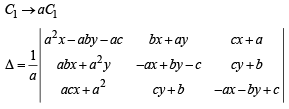 

Applying C₁ → C₁ + bC₂+ cC₃

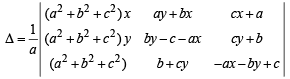
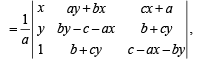
as a² + b² + c² = 1
C₂ → C₂- bC₁ and C₃ → C₃- cC₁

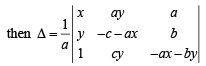
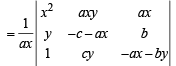
R₁ → R₁ + yR₂+R₃

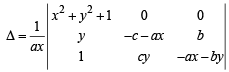
On expanding along R₁

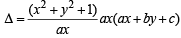
  = (x₂ + y₂ + 1) (ax + by + c)
Given Δ = 0
⇒ ax + by + c = 0, which represents a straight line.
[∵ x₂ + y₂ + 1 ≠ 0, being + ve].

Q.26. A straight line L through the origin meets the lines x + y = 1 and x + y = 3 at P and Q respectively. Through P and Q two straight lines L₁ and L₂ are drawn, parallel to 2x – y = 5 and 3x + y = 5 respectively. Lines L₁ and L₂ intersect at R. Show that the locus of R, as L varies, is a straight line. (2002 - 5 Marks) 

Ans. 

Sol. The  line y = mx meets the given lines in

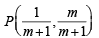and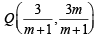  

Hence equation of L₁ is

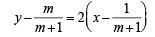
⇒ y – 2x 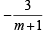– 1 = … (1)

and that of L₂ is

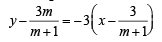
⇒ y + 3x – 3 = 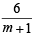… (2)

From (1) and (2)

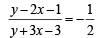
⇒ x – 3y + 5 = 0 which is a straight line.

Q.27. A straigh t lin e L with negative slope passes thr ough the point (8, 2) and cuts the positive coordinate axes at points P and Q. Find the absolute minimum value of OP + OQ, as L varies, where O is the origin. (2002 - 5 Marks) 

Ans. 18

 Sol. Let the equation of the line be (y – 2) = m (x – 8) where m < 0

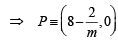and Q ≡ (0, 2- 8m)

Now, OP + OQ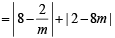 

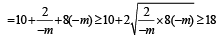
Q.28. The area of the triangle formed by the intersection of a line parallel to x-axis and passing through P (h, k) with the lines y = x and x + y = 2 is 4h². Find the locus of the point P. (2005 - 2 Marks)

Ans. y = 2x +1 or y = -2x +1

Sol. A line passing through P (h, k) and parallel to x-axis is
y = k.                      … (1)
The other two lines given are
y = x                       … (2)
and x + y = 2 … (3)
Let ABC be the Δ formed by the points of intersection of the lines (1), (2) and (3), as shown in the figure.

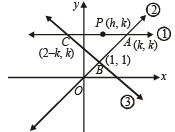
Then A (k, k), B (1, 1), C (2 – k, k)

∴ Area of ΔABC =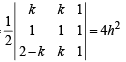 

Operating C₁ – C₂ we get

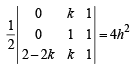
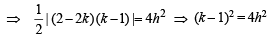
⇒ k – 1 = 2h     or k – 1 = – 2h
⇒ k = 2h + 1 or k = – 2h + 1
∴ Locus of (h, k) is, y = 2x + 1 or y = – 2x + 1.