JEE Advanced (True/False): Quadratic Equation & Inequalities (Inequalities) | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. For every integer n > 1, the inequality 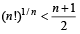 holds.                (1981 - 2 Marks)

Ans. T

Sol. Consider n numbers, namely 1, 2, 3, 4, ....n.
KEY CONCEPT : Now using  A.M. > G.M. for distinct numbers, we get

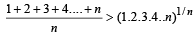
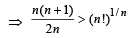
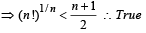
Q.2. The equation 2x² + 3x + 1 = 0 has an irrational root. (1983 - 1 Mark)

Ans. F

Sol. 2x² + 3x + 1 = 0 ⇒ x = -1,-1 /2 both are rational

∴ Statement is  FALSE.

Q.3. If a < b < c < d, then the r oots of the equation

(x – a) (x – c) + 2(x – b) (x – d) = 0 are real and distinct. (1984 - 1 Mark)

Ans. T

Sol. f(x) = (x – a) (x – c) + 2 (x – b) (x – d).

f (a) = + ve; f (b) = – ve ; f(c) = – ve ;  

f (d) = + ve

∴ There exists two real and distinct roots one in the interval (a, b) and other in (c, d). Hence, (True).

Q.4. If n₁, n₂, ......n_p are p positive integers, whose sum is an even number, then the number of odd integers among them is odd. (1985 - 1 Mark)

Ans. F

Sol.Consider N = n₁ + n₂ + n₃+....+ n_p, where N is an even number.
Let k numbers among these p numbers be odd, then p – k are  even numbers.
Now sum of (p – k) even numbers is even and for N to be an even number, sum of k odd numbers must be even which is possible only when k is even.
∴ The given statement is false.

Q.5. If P(x) = ax² + bx + c and Q(x) = –ax² + dx + c, where ac ≠ 0 , then P(x)Q(x)=0 has at least two real roots. (1985 - 1 Mark)

Ans. T

Sol. P(x).Q (x) = (ax² + bx + c) (–ax² + bx + c)

⇒ D₁ = b² – 4ac and D₂ = b² + 4ac

clearly, D1 + D₂ = 2b² ≥ 0

∴ atleast one of D₁ and D₂ is (+ ve). Hence, atleast two real roots.
Thus, (True)

Q.6. If x and y are positive real numbers and m, n are any positive integers, then 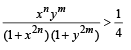 (1989 - 1 Mark)

Ans.  F

Sol. As x and y are positive real numbers and m and n are positive integers

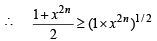and

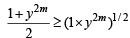
{For two +ve numbers A.M. ≥ G.M.}

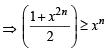....(1)

and 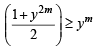....(2)

Multiplying (1) and (2), we get

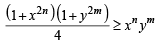
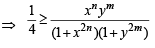
Hence the statement is false.