JEE Advanced Previous Year Questions (2018 - 2023): Conic Sections | Mathematics (Maths) for JEE Main & Advanced PDF Download
2023
Q1: Let P be a point on the parabola y2 = 4ax, where a > 0. The normal to the parabola at P meets the x-axis at a point Q. The area of the triangle PFQ, where F is the focus of the parabola, is 120 . If the slope m of the normal and a are both positive integers, then the pair (a, m) is
(a) (2,3)
(b) (1,3)
(c) (2,4)
(d) (3,4) [JEE Advanced 2023 Paper 1]
Ans: (a)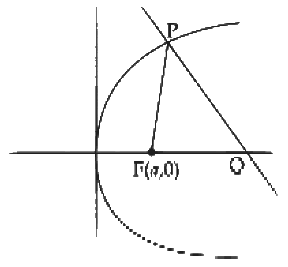
y2 = 4ax
Equation of normal
y = mx - 2am - am3
Point of contact
and Point 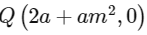
Area of ΔPFQ = 
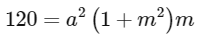
a = 2, m = 3
Satisfies the equation (1), hence (2,3) will be the correct answer.
Q2: Let T1 and T2 be two distinct common tangents to the ellipse 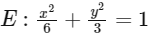 and the parabola
and the parabola 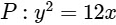 . Suppose that the tangent T1 touches P and E at the points A1 and A2, respectively and the tangent T2 touches P and E at the points A4 and A3, respectively. Then which of the following statements is(are) true?
. Suppose that the tangent T1 touches P and E at the points A1 and A2, respectively and the tangent T2 touches P and E at the points A4 and A3, respectively. Then which of the following statements is(are) true?
(a) The area of the quadrilateral A1A2A3A4 is 35 square units
(b) The area of the quadrilateral A1A2A3A4 is 36 square units
(c) The tangents T1 and T2 meet the x-axis at the point (−3, 0)
(d) The tangents T1 and T2 meet the x-axis at the point (−6, 0) [JEE Advanced 2023 Paper 1]
Ans: (a) and (c)
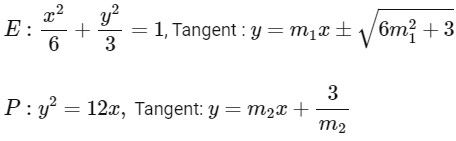
For common tangent
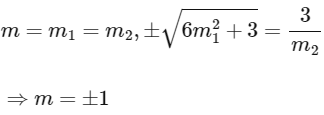
⇒ Equation of common tangents y = x + 3 and y = −x − 3 point of contact for parabola is 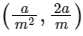
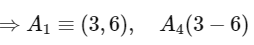
Let A2(x1, y1)⇒ tangent to E is = 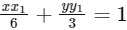
A3 is mirror image of A2 in x-axis ⇒ A3 (-2, -1)
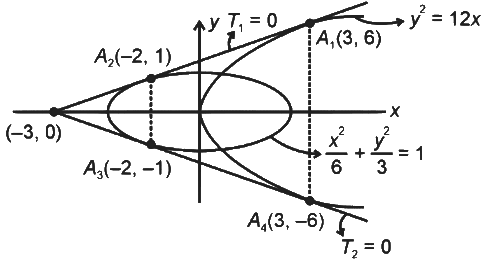
Intersection point of T1 = 0 and T2 = 0 is (−3, 0)
Area of quadrilateral A1A2A3A4 = 12(12 + 2) × 5 = 35 square units
2022
Q1: Consider the hyperbola
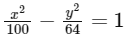 with foci at S and S1, where S lies on the positive x-axis. Let P be a point on the hyperbola, in the first quadrant. Let ∠SPS1 = α, with α < π/2. The straight line passing through the point S and having the same slope as that of the tangent at P to the hyperbola, intersects the straight line S1P at S1. Let δ be the distance of P from the straight line SP1, and β = S1P Then the greatest integer less than or equal to
with foci at S and S1, where S lies on the positive x-axis. Let P be a point on the hyperbola, in the first quadrant. Let ∠SPS1 = α, with α < π/2. The straight line passing through the point S and having the same slope as that of the tangent at P to the hyperbola, intersects the straight line S1P at S1. Let δ be the distance of P from the straight line SP1, and β = S1P Then the greatest integer less than or equal to 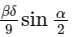 is ________. [JEE Advanced 2022 Paper 2]
is ________. [JEE Advanced 2022 Paper 2]Ans: 7
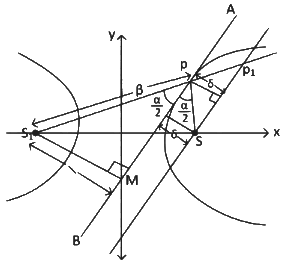
From property we know, tangent and normal is bisector of the angle between focal radii.
∴ Tangent AB divides the angle ∠SPS1= α equal parts.
From another property, we know, if we draw perpendicular to the tangent on the hyperbola from two foci, then product of length of the perpendicular from foci = b2
∴ l × δ = b2
Given hyperbola, 
∴ a2 = 100
and b2 = 64
∴ l × δ = 64 ....... (1)
From right angle triangle S1 MP we get, sinα/2 = l/β
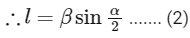
Putting value of l in equation (1), we get
∴ Greatest integer = [7.1] = 7
Q2: Consider the ellipse 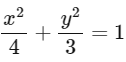 Let H(α, 0), 0 < α < 2, be a point. A straight line drawn through H parallel to the Y-axis crosses the ellipse and its auxiliary circle at points E and F respectively, in the first quadrant. The tangent to the ellipse at the point E intersects the positive x-axis at a point G. Suppose the straight line joining F and the origin makes an angle ϕ with the positive x-axis.
Let H(α, 0), 0 < α < 2, be a point. A straight line drawn through H parallel to the Y-axis crosses the ellipse and its auxiliary circle at points E and F respectively, in the first quadrant. The tangent to the ellipse at the point E intersects the positive x-axis at a point G. Suppose the straight line joining F and the origin makes an angle ϕ with the positive x-axis.
The correct option is:
A(I)→(R);(II)→(S);(III)→(Q);(IV)→(P)
B(I)→(R); (II)→(T);(III)→(S);(IV)→(P)
C(I)→(Q);(II)→(T);(III)→(S);(IV)→(P)
D(I)→(Q); (II)→(S); (III)→(Q); (IV)→(P) [JEE Advanced 2022 Paper 1]
Ans: (c)
Given, 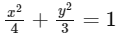
Let 
Tangent at 
to the ellipse is 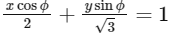
This intersect x-axis at 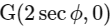
Area of triangle FGH = 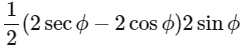
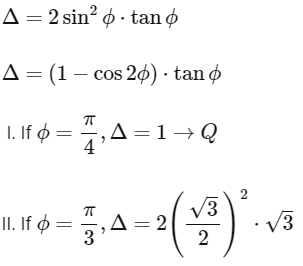
= 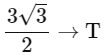
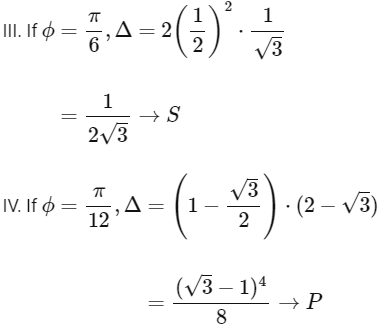
Q3: Consider the parabola y2 = 4x. Let S be the focus of the parabola. A pair of tangents drawn to the parabola from the point P = (−2, 1) meet the parabola at P1 and P2. Let Q1 and Q2 be points on the lines SP1 and SP2 respectively such that PQ1 is perpendicular to SP1 and PQ2 is perpendicular to SP2. Then, which of the following is/are TRUE?
(a) SQ1 = 2
(b) 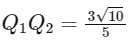
(c) PQ1 = 3
(d) SQ2 = 1 [JEE Advanced 2022 Paper 1]
Ans: (b), (c) & (d)
Let P1(t2, 2t) then tangent at P1 will be
ty = x + t2
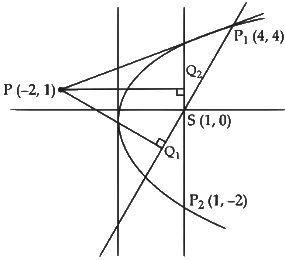
Since, it passes through (−2,1)
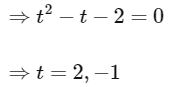
So, we get point P1(4, 4) and P2(1, −2)
Now finding the equation of SP1 : 4x − 3y − 4 = 0
And equation of SP2: x − 1= 0
Now finding the point by foot of point on line formula,
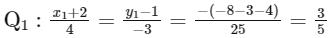
We get, 
Now using the distance formula we get,
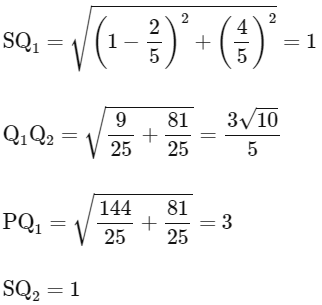
Hence, option (B, C, D) are correct.
2021
Q1: Let E be the ellipse 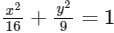 . For any three distinct points P, Q and Q' on E, let M(P, Q) be the mid-point of the line segment joining P and Q, and M(P, Q') be the mid-point of the line segment joining P and Q'. Then the maximum possible value of the distance between M(P, Q) and M(P, Q'), as P, Q and Q' vary on E, is _______. [JEE Advanced 2021 Paper 2]
. For any three distinct points P, Q and Q' on E, let M(P, Q) be the mid-point of the line segment joining P and Q, and M(P, Q') be the mid-point of the line segment joining P and Q'. Then the maximum possible value of the distance between M(P, Q) and M(P, Q'), as P, Q and Q' vary on E, is _______. [JEE Advanced 2021 Paper 2]
Ans: 4
As we know that, in a triangle, sides joining the mid-points of two sides is half and parallel to the third side.
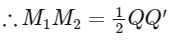

Maximum value of QQ' is AA'
Hence, maximum value of 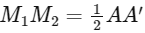
= 4
Q2: Let E denote the parabola y2 = 8x. Let P = (−2, 4), and let Q and Q' be two distinct points on E such that the lines PQ and PQ' are tangents to E. Let F be the focus of E. Then which of the following statements is(are) TRUE?
(a) The triangle PFQ is a right-angled triangle
(b) The triangle QPQ' is a right-angled triangle
(c) The distance between P and F is 5√2
(d) F lies on the line joining Q and Q' [JEE Advanced 2021 Paper 2]
Ans: (a), (b) & (d)
Given, E : y2 = 8x .... (i)
and P ≡ (−2, 4)
Now, directrix of Eq. (i) is x = −2
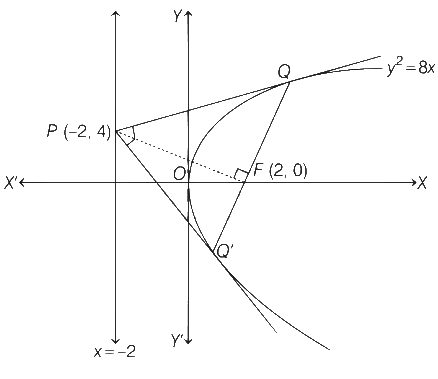
So, point P(−2, 4) lies on the directrix of parabola y2 = 8x. Hence, 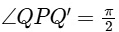 (by the definition of director circle) and chord QQ' is a focal chord and segment PQ subtends a right angle at the focus.
(by the definition of director circle) and chord QQ' is a focal chord and segment PQ subtends a right angle at the focus.
Slope of PF = −1 (∵ PF ⊥ QQ')
Now, slope of 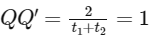

2020
Q1: Let a, b and λ be positive real numbers. Suppose P is an end point of the latus return of the
parabola y2 = 4λx, and suppose the ellipse  passes through the point P. If the tangents to the parabola and the ellipse at the point P are perpendicular to each other, then the eccentricity of the ellipse is
passes through the point P. If the tangents to the parabola and the ellipse at the point P are perpendicular to each other, then the eccentricity of the ellipse is
(a) 1/√2
(b) 1/2
(c) 1/3
(d) 2/5 [JEE Advanced 2020 Paper 1]
Ans: (a)
Equation of given parabola is
y2 = 4λx ....(i)
So the end point of the latus rectum of the parabola (i), P(λ, 2λ) and the given ellipse 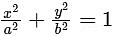 , passes through point P(λ, 2λ).
, passes through point P(λ, 2λ).
On differentiating the equation of parabola, w.r.t. 'x', we get 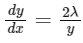
∴ Slope of tangent to the parabola at point P is m1 = 1
Similarly, on differentiating the equation of given ellipse, 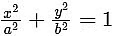 , w.r.t.x, we get
, w.r.t.x, we get 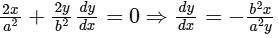
∴ Slope of tangent to the ellipse at point P is m2 = 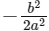
∵ It is given that the tangents are perpendicular to each other. So, m1m2 = -1
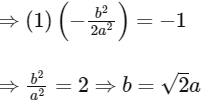
∴ Eccentricity of ellipse  will be
will be
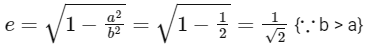
Q2: Let a and b be positive real numbers such that a > 1 and b < a. Let P be a point in the first quadrant that lies on the hyperbola 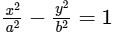 . Suppose the tangent to the hyperbola at P passes through the point (1, 0), and suppose the normal to the hyperbola at P cuts off equal intercepts on the coordinate axes. Let Δ denote the area of the triangle formed by the tangent at P, the normal at P and the X-axis. If e denotes the eccentricity of the hyperbola, then which of the following statements is/are TRUE?
. Suppose the tangent to the hyperbola at P passes through the point (1, 0), and suppose the normal to the hyperbola at P cuts off equal intercepts on the coordinate axes. Let Δ denote the area of the triangle formed by the tangent at P, the normal at P and the X-axis. If e denotes the eccentricity of the hyperbola, then which of the following statements is/are TRUE?
(a) 1 < e < √2
(b) √2 < e < 2
(c) Δ = a4
(d) Δ = b4 [JEE Advanced 2020 Paper 2]
Ans: (a) & (d)
Equation of given hyperbola is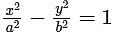 , a > b and a > 1
, a > b and a > 1
Let point P(a secθ, b tanθ) on the hyperbola in first quadrant i.e., 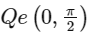 .
.
Now equation of tangent to the hyperbola at point P is
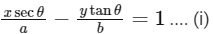
∵ The tangent (i) passes through point A(1, 0)
So, 
and equation of normal to the hyperbola at point P having slope is  , as normal cuts off equal intercepts on the coordinate axes, so slope must be −1.
, as normal cuts off equal intercepts on the coordinate axes, so slope must be −1.
Therefore,  = -1
= -1

∵ The eccentricity of hyperbola
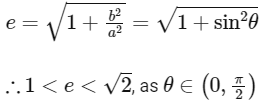
And the area of required triangle is, which is isosceles is
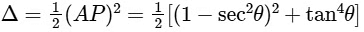
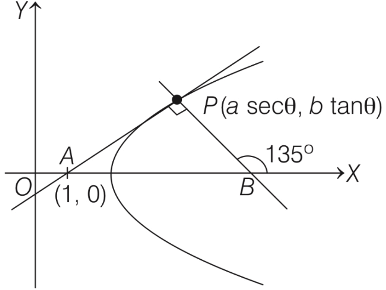
= 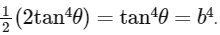
2019
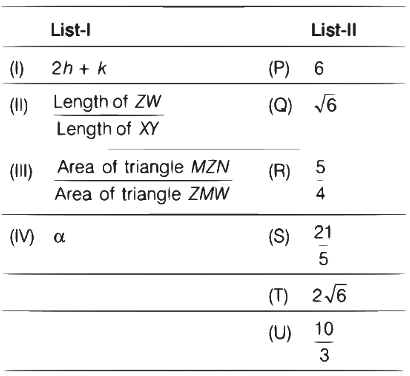
Q1: Let the circles C1 : x2 + y2 = 9 and C2 : (x − 3)2 + (y − 4)2 = 16, intersect at the points X and Y. Suppose that another circle C3 : (x − h)2 + (y − k)2 = r2 satisfies the following conditions :
(i) Centre of C3 is collinear with the centres of C1 and C2.
(ii) C1 and C2 both lie inside C3 and
(iii) C3 touches C1 at M and C2 at N.
Let the line through X and Y intersect C3 at Z and W, and let a common tangent of C1 and C3 be a tangent to the parabola x2 = 8αy.
There are some expression given in the List-I whose values are given in List-II below.
(a) (III), (R)
(b) (IV), (S)
(c) (I), (P)
(d) (IV), (U) [JEE Advanced 2019 Paper 2]
Ans: (b)
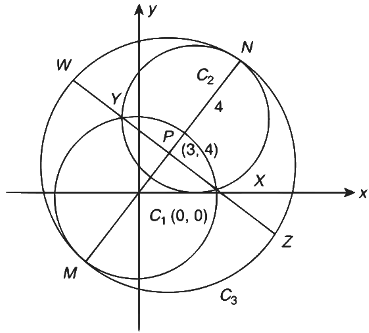
It is given that, the centres of circles C1, C2 and C3 are co-linear,

and MN is the length of diameter of circle C3, so
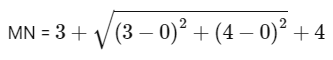
= 3 + 5 + 4 = 12
So, radius of circle C3, r = 6 ......(ii)
Since, the circle C3 touches C1 at M and C2 at N, so
|C1 C3| = |r − 3|
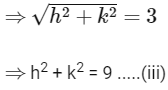
From Eqs. (i) and (iii), we get

So, 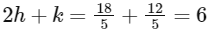
Now, equation common chord XY of circles C1 and C2 is
C1 − C2 = 0
⇒ 6x + 8y = 18
⇒ 3x + 4y = 9 ....(iv)
Now, PY2 = GY2 − GP2 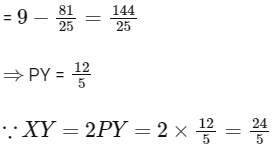
Similarly, equation of ZW is 3x + 4y = 9.
Now, So, length of perpendicular from C3 to
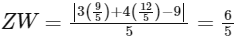
So, 
{∵ C3W = r = 6}
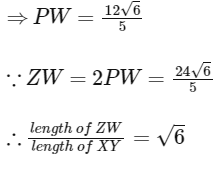
Now, area of

and area of ΔZMW = 1/2(ZW) (MP)
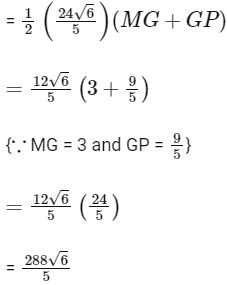
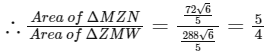
∵ Common tangent of circles C1 and C3 is C1 − C3 = 0
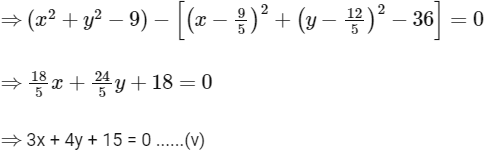
∵ Tangent (v) is also touches the parabola x2 = 8αy,

So combination (iv), (S) is only incorrect.
Hence, option (b) is correct.
2018
Q1: Let 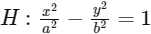 , where a > b > 0, be a hyperbola in the XY-plane whose conjugate axis LM subtends an angle of 60∘ at one of its vertices N. Let the area of the ΔLMN be 4√3.
, where a > b > 0, be a hyperbola in the XY-plane whose conjugate axis LM subtends an angle of 60∘ at one of its vertices N. Let the area of the ΔLMN be 4√3. 
(b) P → 4 ; Q → 3 ; R → 1 ; S → 2
(c) P → 4 ; Q → 1 ; R → 3 ; S → 2
(d) P → 3 ; Q → 4 ; R → 2 ; S → 1 [JEE Advanced 2018 Paper 2]
Ans: (b)
We have,
Equation of hyperbola
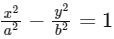

It is given,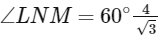
and Area of ΔLMN = 4√3
Now, ΔLMN is an equilateral triangle whose sides is 2b .
Area of ΔLMN = 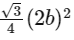
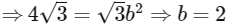
Also, area of ΔLMN = 1/2 a(2b) = ab

(P) Length of conjugate axis = 2b = 2(2) = 4 (Q)
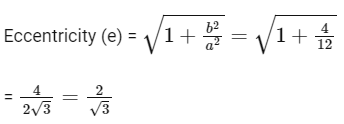
(R) Distance between the foci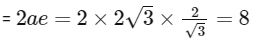
(S) The length of latusrectum
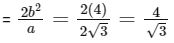
P → 4; Q → 3; R → 1; S → 2
Hence, option (b) is correct.
Q2: Let S be the circle in the XY-plane defined the equation x2 + y2 = 4.
Let E1E2 and F1F2 be the chords of S passing through the point P0 (1, 1) and parallel to the X-axis and the Y-axis, respectively. Let G1G2 be the chord of S passing through P0 and having slope−1. Let the tangents to S at E1 and E2 meet at E3, then tangents to S at F1 and F2 meet at F3, and the tangents to S at G1 and G2 meet at G3. Then, the points E3, F3 and G3 lie on the curve
(a) x + y = 4
(b) (x − 4)2 + (y − 4)2 = 16
(c) (x − 4)(y − 4) = 4
(d) xy = 4 [JEE Advanced 2018 Paper 1]
Ans: (a)
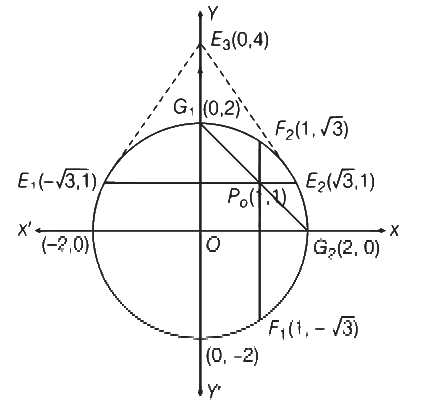
Equation of tangent at 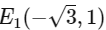 is
is
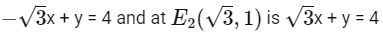
Intersection point of tangent at E1 and E2 is (0, 4)
∴ Coordinates of E3 is (0, 4)
Similarly, equation of tangent at
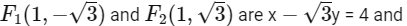
x + √3y = 4, respectively and intersection point
is (4, 0), i.e., F3(4, 0) and equation of tangent at G1(0, 2) and G2(2, 0) are 2y = 4 and 2x = 4, respectively and intersection point
is (2, 2) i.e., G3(2, 2).
Point E3(0, 4), F3(4, 0) and G3(2, 2) satisfies the line x + y = 4.
Q3: Let S be the circle in the XY-plane defined the equation x2 + y2 = 4.
Let P be a point on the circle S with both coordinates being positive. Let the tangent to S at P intersect the coordinate axes at the points M and N. Then, the mid-point of the line segment MN must lie on the curve
(a) (x + y)2 = 3xy
(b) x2/3 + y2/3 = 24/3
(c) x2 + y2 = 2xy
(d) x2 + y2 = x2y2 [JEE Advanced 2018 Paper 1]
Ans: (d)
We have,
x2 + y2 = 4
Let P(2 cosθ, 2 sinθ) be a point on a circle.
∴ Tangent at P is
2 cosθx + 2 sinθy = 4
⇒ x cosθ + y sinθ = 2
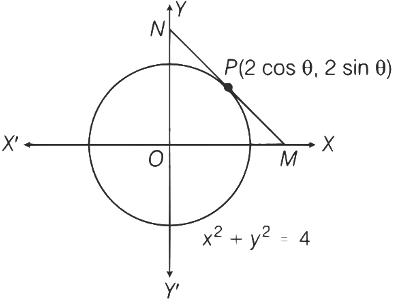
The coordinates at 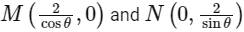
Let (h, k) is mid-point of MN

∴ Mid-point of MN lie on the curve
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|

|
Explore Courses for JEE exam
|

|

















