JEE Advanced Previous Year Questions (2018 - 2023): Matrices and Determinants | Mathematics (Maths) for JEE Main & Advanced PDF Download
2023
Q1: Let 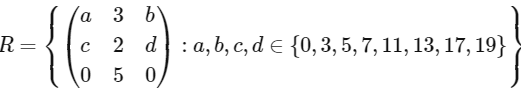 .
.
Then the number of invertible matrices in R is : [JEE Advanced 2023 Paper 2]
Ans: 3780
Q2: Let α,β and γ be real numbers. Consider the following system of linear equations
x + 2y + z = 7
x + αz = 11
2x − 3y + βz = γ
Match each entry in List-I to the correct entries in List-II. [JEE Advanced 2023 Paper 1]
(a) (P)→(3) (Q)→(2) (R)→(1) (S)→(4)
(b) (P)→(3) (Q)→(2) (R)→(5) (S)→(4)
(c) (P)→(2) (Q)→(1) (R)→(4) (S)→(5)
(d) (P)→(2) (Q)→(1) (R)→(1) (S)→(3)
Ans: (a)
x + 2y + z = 7
x + αz = 11
2x − 3y + βz = γ
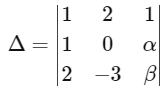
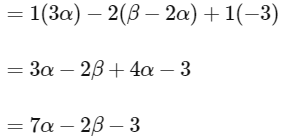
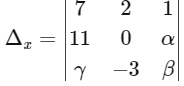

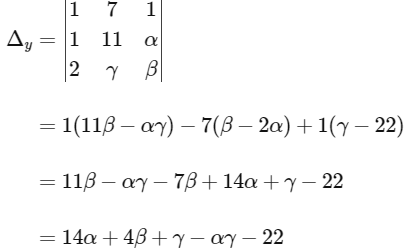
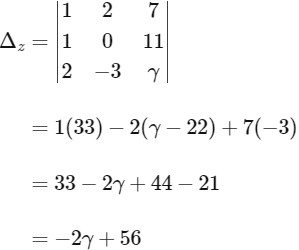
For unique solution Δ ≠ 0
For infinite solution
Δ = Δx = Δy = Δz = 0
For no solution Δ=0 and atleast one in Δx, Δy, Δz is non zero.
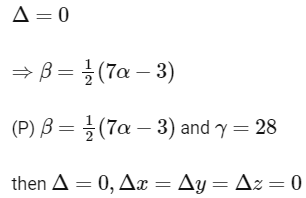
∴ Infinite solution
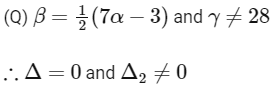
⇒ No solution.]
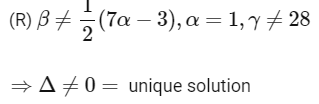
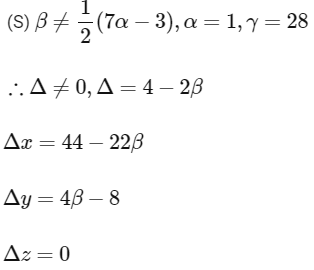
∴ x = 11, y = -2, z = 0 is the solution.
Q3: Let M = (aij),i,j ∈ {1, 2, 3}, be the 3 × 3 matrix such that aij = 1 if j + 1 is divisible by i, otherwise aij = 0. Then which of the following statements is(are) true? [JEE Advanced 2023 Paper 2]
(a) M is invertible
(b) There exists a nonzero column matrix 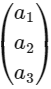 such that
such that 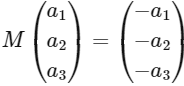
(c) The set {X∈ 𝕽3: MX = 0} ≠ {0}, where 0 = 
(d) The matrix (M −2I) is invertible, where I is the 3 × 3 identity matrix
Ans: (b) & (c)
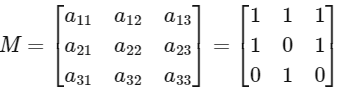
|M| = −1 + 1 = 0 ⇒M is singular so non-invertible ⇒ [A] is wrong. 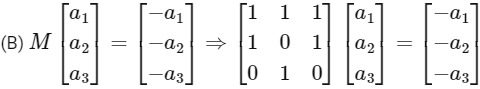
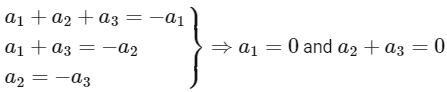
infinite solutions exists [B] is correct.
Option (D) ;
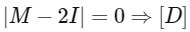 is wrong
is wrong
Option (C);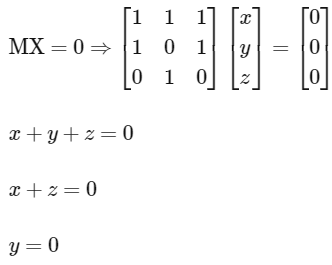
∴ Infinite solution
Option (C) is correct
2022
Q1: Let β be a real number. Consider the matrix
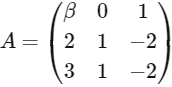
If  is a singular matrix, then the value of 9β is _________. [JEE Advanced 2022 Paper 2]
is a singular matrix, then the value of 9β is _________. [JEE Advanced 2022 Paper 2]
Ans: 3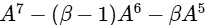 is a singular matrix. So determinant of this matrix equal to zero.
is a singular matrix. So determinant of this matrix equal to zero.
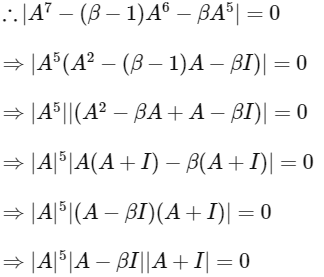
Now given,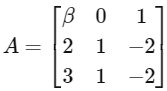
∴ |A| = 2 - 3 = -1
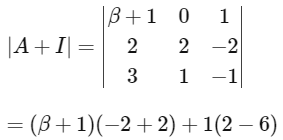
= -4
We get |A| ≠ 0 and |A + I| ≠ 0
∴ |A|5|A − βI| |A + I| = 0 is possible only when |A − βI| = 0
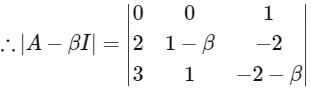
= 2 - 3 - 3β
∴ 2 - 3 +3β
⇒ 3β = 1
⇒ 9β = 3
Q2: If 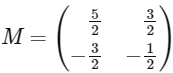 , then which of the following matrices is equal to M2022? [JEE Advanced 2022 Paper 2]
, then which of the following matrices is equal to M2022? [JEE Advanced 2022 Paper 2]
(a) 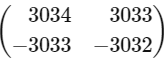
(b) 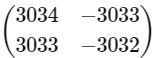
(c) 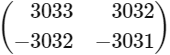
(d) 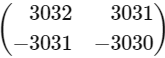
Ans: (a)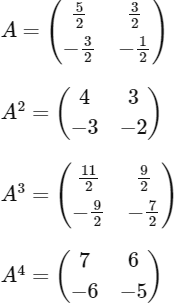
and so on
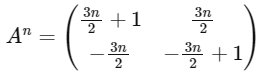
Now,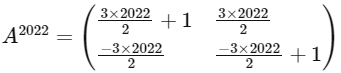
= 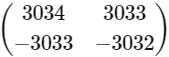
∴ Option (A) is correct
Q3: Let p,q,r be nonzero real numbers that are, respectively, the 10th ,100th and 1000th terms of a harmonic progression. Consider the system of linear equations
x + y + z = 1
10x + 100y + 1000z = 0
qrx + pry + pqz = 0
The correct option is:
(a) (I) → (T); (II) → (R); (III) → (S); (IV) → (T)
(b) (I) → (Q); (II) → (S); (III) → (S); (IV) → (R)
(c) (I) →(Q); (II) → (R); (III) →(P); (IV) → (R)
(d) (I) → (T); (II) → (S); (III) → (P); (IV) → (T)
Ans: (b)
Given
x + y + z = 1 ----(1)
10x + 100y + 1000z = 0 ----(2)
qrx + pry + pqz = 0 ----(3)
Now equation (3) can be re-written as
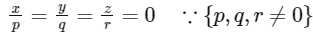
Now given p,q and r are th th 10th ,100th and th 1000th term of an. H.P.,
So let 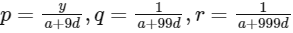
Now from equation (3)
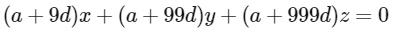
Now from and (1), (2) and (3) we get
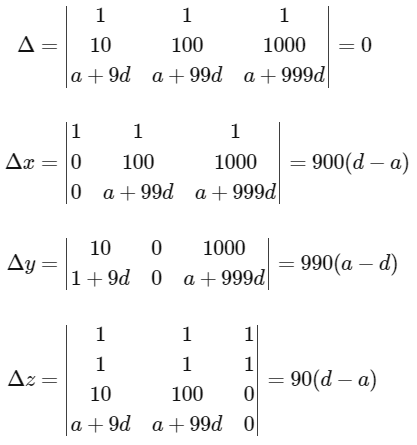
(I) If 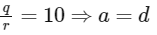
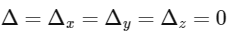
And equation (1) and equation (2) represents non-parallel plane equation (2) and equation (3) represents same plane
⇒ Infinitely many solutions.
Now finding solution by taking z = λ then
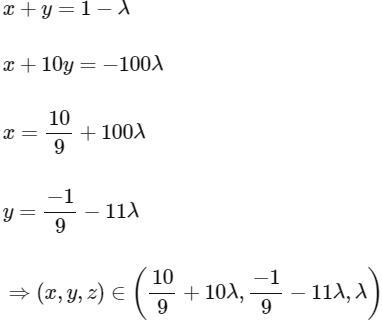
So P is not valid for any value of λ → Q
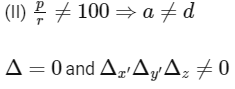
So no solution.
(II) II → S
(IV) If 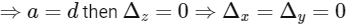
So infinitely many solutions.
IV → R
2021
Q1: For any 3 × 3 matrix M, let |M| denote the determinant of M. Let I be the 3 × 3 identity matrix. Let E and F be two 3 × 3 matrices such that (I − EF) is invertible. If G = (I − EF)−1, then which of the following statements is (are) TRUE? [JEE Advanced 2021 Paper 1]
(a) | FE | = | I − FE| | FGE |
(b) (I − FE)(I + FGE) = I
(c) EFG = GEF
(d) (I − FE)(I − FGE) = I
Ans: (a), (b) & (c)
∵ I − EF = G−1
⇒ G − GEF = I ..... (i)
and G − EFG = I ..... (ii)
Clearly, GEF = EFG → option (c) is correct.
Also, (I − FE) (I + FGE)
= I − FE + FGE − FEFGE
= I − FE + FGE − F(G − I) E
= I − FE + FGE − FGE + FE
= I → option (b) is correct but option (d) is incorrect.
∵ (I − FE) (I − FGE) = I − FE − FGE + F(G − I) E
= I − 2FE
Now, (I − FE) (− FGE) = − FE
⇒ | I − FE | | FGE | = | FE |
→ option (a) is correct.
Q2: For any 3 × 3 matrix M, let | M | denote the determinant of M. Let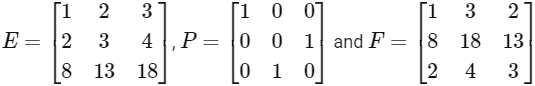
If Q is a nonsingular matrix of order 3 × 3, then which of the following statements is(are) TRUE?
(a) F = PEP and 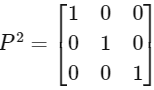
(b) | EQ + PFQ−1 | = | EQ | + | PFQ−1 |
(c) | (EF)3 | > | EF |2
(d) Sum of the diagonal entries of P−1EP + F is equal to the sum of diagonal entries of E + P−1FP [JEE Advanced 2021 Paper 1 ]
Ans: (a), (b) & (d)
For Option (a):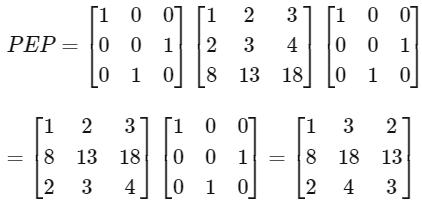
= F
and 
Hence, option (a) is correct.
For option (b)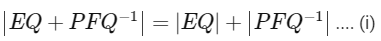
∵ | E | = 0 and | F | = 0 and | Q | ≠ 0
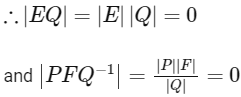
Let, 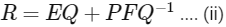
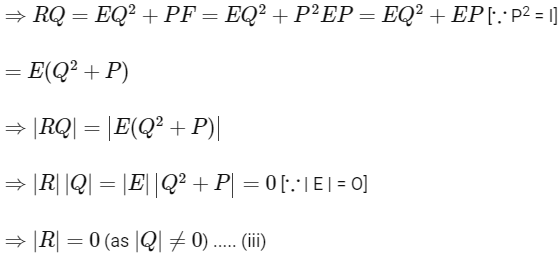
From Eqs. (ii) and (iii), we get Eq. (i) is true.
Hence, option (b) is correct.
For option (c)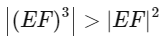
i.e. 0 > 0 which is false.
For option (d)
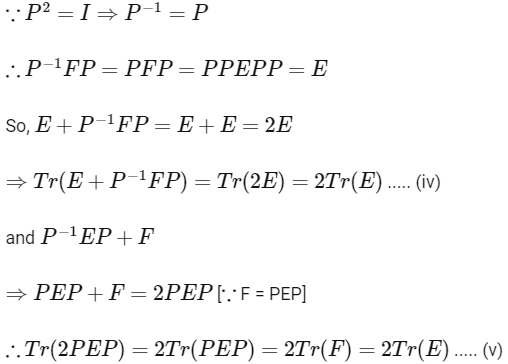
From Eqs. (iv) and (v) option (d) is also correct.
2020
Q1: The trace of a square matrix is defined to be the sum of its diagonal entries. If A is a 2 × 2 matrix such that the trace of A is 3 and the trace of A3 is −18, then the value of the determinant of A is ______. [JEE Advanced 2020 Paper 2]
Ans: 5
Let a square matrix 'A' of order 2 × 2, such that tr(A) = 3, is
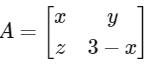
So, 
= 
∴ 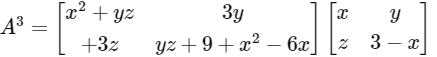
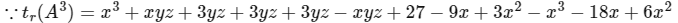

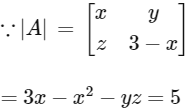
Q2: Let M be a 3 × 3 invertible matrix with real entries and let I denote the 3 × 3 identity matrix. If M−1 = adj(adj M), then which of the following statements is/are ALWAYS TRUE? [JEE Advanced 2020 Paper 1]
(a) M = I
(b) det M = 1
(c) M2 = I
(d) (adj M)2 = I
Ans: (b), (c) & (d)
It is given that matrix M be a 3 × 3 invertible matrix, such that
M−1 = adj(adj M) ⇒ M−1 = |M| M
(∵ for a matrix A of order 'n' adj(adjA) = |A|n−2 A}
⇒ M−1 M = |M|M2
⇒ M2|M| = I .....(i)
∵ det(M2 |M|) = det(I) = 1
⇒ |M|3|M|2 = 1
⇒ |M| = 1 .....(ii)
from Eqs. (i) and (ii), we get
M2 = I
As, adj M = |M|M−1 = M
⇒ (adj M)2 = M2 (adj M)2 = I
2019
Q1: Suppose 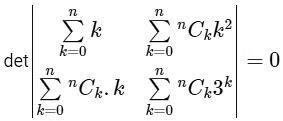 holds for some positive integer n. Then
holds for some positive integer n. Then 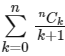 equals ____________. [JEE Advanced 2019 Paper 2]
equals ____________. [JEE Advanced 2019 Paper 2]
Ans: 6.20
It is given that,

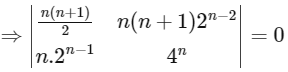
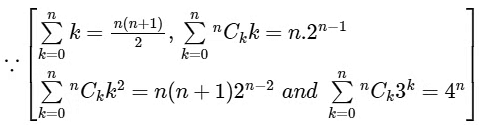
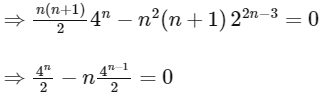
⇒ n = 4
= 1/5 (32 - 1) = 31/5
= 6.20
Q2: Let 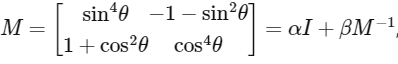 , where α = α(θ) and β = β(θ) are real numbers, and I is the 2 × 2 identity matrix. If α* is the minimum of the set {α(θ) : θ ∈ [0, 2π)} and {β(θ) : β ∈ [0, 2π)}, then the value of α* + β* is
, where α = α(θ) and β = β(θ) are real numbers, and I is the 2 × 2 identity matrix. If α* is the minimum of the set {α(θ) : θ ∈ [0, 2π)} and {β(θ) : β ∈ [0, 2π)}, then the value of α* + β* is
(a) -17/16
(b) -31/16
(c) -37/16
(d) -29/16
Ans: (d)
It is given that matrix
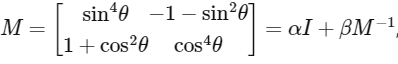 , where α = α(θ) and β = β(θ) are real numbers, and I is the 2 × 2 identity matrix.
, where α = α(θ) and β = β(θ) are real numbers, and I is the 2 × 2 identity matrix.
Now,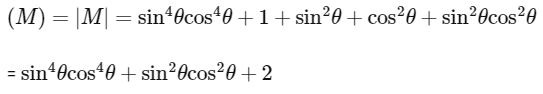
and 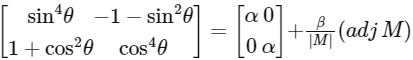
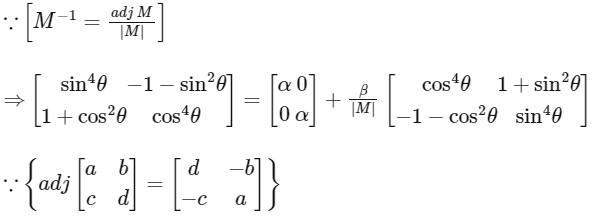

Now, 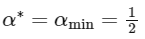
and, 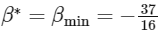
∵ α is minimum at sin2(2θ) = 1 and β is minimum at sin2(2θ) = 1
So, 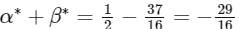
2018
Q1: Let P be a matrix of order 3 × 3 such that all the entries in P are from the set {−1, 0, 1}. Then, the maximum possible value of the determinant of P is ______ . [JEE Advanced 2018 Paper 2 ]
Ans: 4
Let 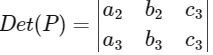
= 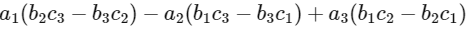
Now, maximum value of Det (P) = 6
If  and
and 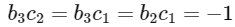
But it is not possible as
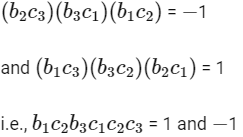
Similar contradiction occurs when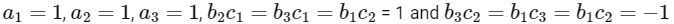
Now, for value to be 5 one of the terms must be zero but that will make 2 terms zero which means answer cannot be 5
Now,

Hence, maximum value is 4
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|

|
Explore Courses for JEE exam
|

|

















