JEE Advanced Previous Year Questions (2018 - 2023): Permutations and Combinations | Mathematics (Maths) for JEE Main & Advanced PDF Download
2022
Q1: Consider 4 boxes, where each box contains 3 red balls and 2 blue balls. Assume that all 20 balls are distinct. In how many different ways can 10 balls be chosen from these 4 boxes so that from each box at least one red ball and one blue ball are chosen ?
(a) 21816
(b) 85536
(c) 12096
(d) 156816 [JEE Advanced 2022 Paper 2]
Ans: (a)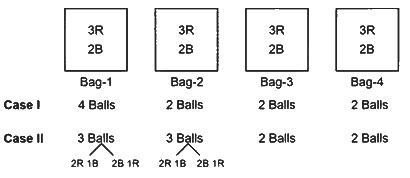
Among four bags from one bag 4 balls are taken. Number of ways of choosing one bag from 4 bags = 4C1
From this bag number of ways of taking 4 balls are
(a) 3 Red and 1 Blue balls, which can be chosen in
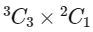ways.(b) 2 Red and 2 Blue balls, which can be chosen in
.∴ Total number of ways of choosing this 4 balls from this bag = 4C1
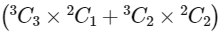
Now, two balls are taken from remaining three bags.
From each bag two balls can be taken in 3C1 × 2C1 ways.So, for three bags two balls can be taken in (3C1 × 2C1)3 ways.
∴ Total number of ways of chosing 10 balls from these four bags
=
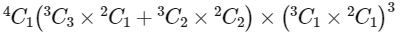
Among four bags from two bags 3 balls are taken. Number of ways of chosing two bags from 4 bags = 4C2
From each bag, number of ways of taking 3 balls are
(a) 2 Red and 1 Blue balls, which can be chosen in 3C2 × 2C1 ways.
(b) 1 Red and 2 Blue balls, which can be chosen in 3C1 × 2C2 ways.
So, for two bags three balls can be taken in (3C2 × 2C1 + 3C1 × 2C2)2 ways.
∴ Total number of ways of choosing this 3 balls from this two bags = 4C2(3C2 × 2C1 + 3C1 × 2C2)2
Now, two balls are taken from remaining two bags.
From each bag two balls can be taken in 3C1 × 2C1 ways.
So, for two bags two balls can be taken in (3C1 × 2C1)2 ways.
∴ Total number of ways of chosing 10 balls from these four bags
=
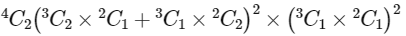From Case 1 and Case 2, total number of ways of chosing 10 balls from these 4 boxes so that from each box at least one red ball and one blue ball are chosen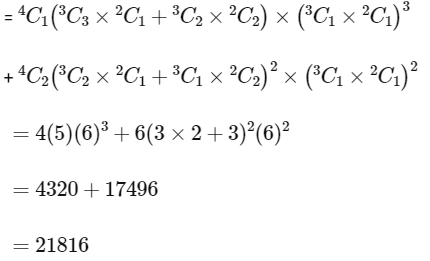
Q2: The number of 4-digit integers in the closed interval [2022, 4482] formed by using the digits 0, 2, 3, 4, 6, 7 is _________. [JEE Advanced 2022 Paper 1]
Ans: 569
This is a 4-digit integer whose 0th digit called D, 10th digit called C, 100th digit called B and 1000th digit called A.
Given range for possible number is 2022 to 4482.
So, position A can have digits 2, 3 or 4.
0, 6 and 7 can't put in A as number starts with 0, 6 or 7 don't fall in the range between 2022 to 4482.
So, Position A can be filled with 2, 3 or 4 in 3C1=3 ways.
Position B can be filled by one of 0, 2, 3, 4, 6, 7
So, total possible ways for position B = 6C1=6 ways
Similarly, Position C can be filled in 6C1=6 ways
Position D can be filled in 6C1=6 ways
∴ Total possible integer numbers starting with 2 or 3 or 4
= 3 × 6 × 6 × 6 = 3 × 216 = 648
Now lets find those numbers which starts with 2 and 4 but don't fall in the range between 2022 to 4482.
Situation 1: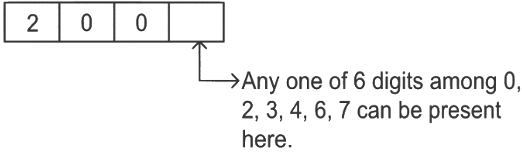
∴ Total possible numbers starting with 200 are = 6
Situation 2:
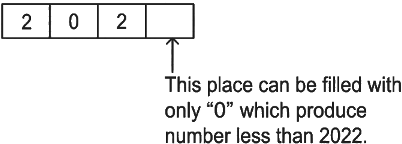
∴ Total possible number in this case = 1
Situation 3:
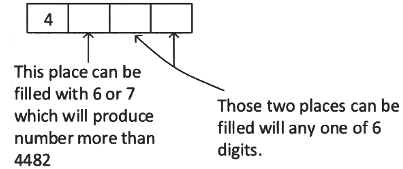
Total numbers in this case = 2 × 6 × 6 = 72
∴ Total number that don't fall in the range 2022 to 4482 which starts with 2 or 4 are
= 6 + 1 + 72=79
∴ Total numbers falls in the range 2022 to 4482
=648 − 79
=569
2020
Ans: 495
Let the engineer visits the factory first time after x1 days to 1 June, second time after x2 days to first visit and so on.
∴ x1 + x2 + x3 + x4 + x5 = 11
where x1, x5 ≥ 0 and x2, x3, x4 ≥ 1 according to the requirement of the question.
Now, let x2 = a + 1, x3 = b + 1 and x4 = c + 1 where a, b, c ≥ 0
∴ New equation will be
x1 + a + b + c + x5 = 8
Now, the number of all possible ways in which the engineer can made visits is equals to the non-negative integral solution of equation
x1 + a + b + c + x5 = 8, and it is equal to
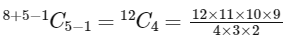
=495
Q2: In a hotel, four rooms are available. Six persons are to be accommodated in these four rooms in such a way that each of these rooms contains at least one person and at most two persons. Then the number of all possible ways in which this can be done is .......... [JEE Advanced 2020 Paper 2]
Ans: 1080
The groups of persons can be made only in 2, 2, 1, 1
∴ So the number of required ways is equal to number of ways to distribute the 6 distinct objects in group sizes 1, 1, 2 and 2
= 
= 360 x 3 = 1080
2019
Q1: Let |X| denote the number of elements in a set X. Let S = {1, 2, 3, 4, 5, 6} be a sample space, where each element is equally likely to occur. If A and B are independent events associated with S, then the number of ordered pairs (A, B) such that 1 ≤ |B| < |A|, equals ............. [JEE Advanced 2019 Paper 2]
Ans: 1523
Given sample space S = {1, 2, 3, 4, 5, 6} and let there are i elements in set A and j elements in set B.
Now, according to information 1 ≤ j < i ≤ 6.
When number of element in set B = 1 then number of elements in set A can be 2 or 3 or 4 or 5 or 6. Number of such pairs of A and B in this case
= 6C1[6C2 + 6C3 + 6C4 + 6C5 + 6C6]
When number of element in set B = 2 then number of elements in set A can be 3 or 4 or 5 or 6. Number of such pairs of A and B in this case
= 6C2[ 6C3 + 6C4 + 6C5 + 6C6]
When number of element in set B = 3 then number of elements in set A can be 4 or 5 or 6. Number of such pairs of A and B in this case
= 6C3[ 6C4 + 6C5 + 6C6]
When number of element in set B = 4 then number of elements in set A can be 5 or 6. Number of such pairs of A and B in this case
= 6C4[ 6C5 + 6C6]
When number of element in set B = 5 then number of elements in set A can be 6. Number of such pairs of A and B in this case
= 6C5[ 6C6]
So, total number of ways of choosing sets A and B
= 6C1[6C2 + 6C3 + 6C4 + 6C5 + 6C6]
+ 6C2[ 6C3 + 6C4 + 6C5 + 6C6]
+ 6C3[ 6C4 + 6C5 + 6C6]
+ 6C4[ 6C5 + 6C6]
+ 6C5[ 6C6]
= Sum of all possible products of two terms from
6C1, 6C2, 6C3, ......., 6C6 = p(Assume)
Now we know,
(6C1 + 6C2 + .....+ 6C6)2
= [ (6C1)2 + (6C2)2+ ....+ (6C6)2] + 2[6C16C2 + 6C16C3 + ... +6C16C6
+ 6C26C3 + 6C26C4 + ... +6C26C6+ ....+ 6C56C6]
⇒ (6C1 + 6C2 + .....+ 6C6)2
= [ (6C1)2 + (6C2)2+ ....+ (6C6)2] + 2(p)
⇒ (26 - 6C0)2 = [ 12C6 - (6C0)2 ] + 2p
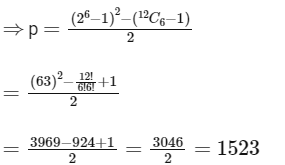
Q2: Let α and β be the roots of x2 − x − 1 = 0, with α > β. For all positive integers n, define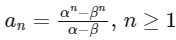
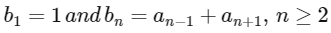
Then which of the following options is/are correct?
(a)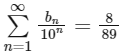 
(b) bn = αn + βn for all n ≥ 1
(c) a1 + a2 + a3 + ... + an = an+2 − 1 for all n ≥ 1
(d)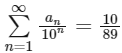 
[JEE Advanced 2019 Paper 1]
Ans: (b), (c) & (d)
Given quadratic equation
x2 − x − 1 = 0, with α > β
So,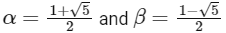 
and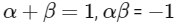 
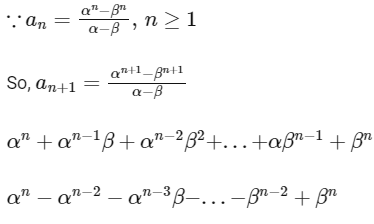
So, option (b) is correct.
Now,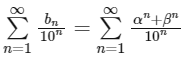 
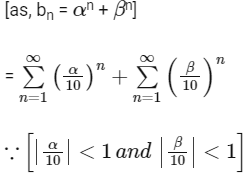
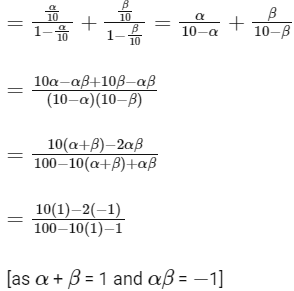
= 12/89
So, option (a) is not correct.
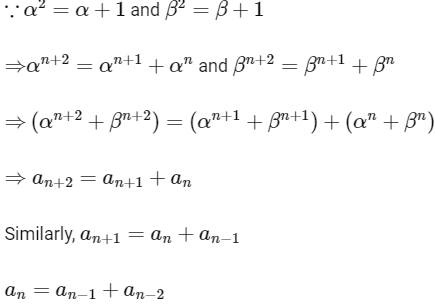
On adding, we get
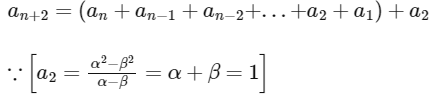
So, option (c) is also correct.
And Now,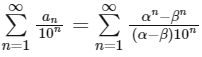 
Hence, options (b), (c) and (d) are correct.
2018
Q1: In a high school, a committee has to be formed from a group of 6 boys M1, M2, M3, M4, M5, M6 and 5 girls G1, G2, G3, G4, G5.
(i) Let α1 be the total number of ways in which the committee can be formed such that the committee has 5 members, having exactly 3 boys and 2 girls.
(ii) Let α2 be the total number of ways in which the committee can be formed such that the committee has at least 2 members, and having an equal number of boys and girls.
(iii) Let α3 be the total number of ways in which the committee can be formed such that the committee has 5 members, at least 2 of them being girls.
(iv) Let α4 be the total number of ways in which the committee can be formed such that the committee has 4 members, having at least 2 girls such that both M1 and G1 are NOT in the committee together.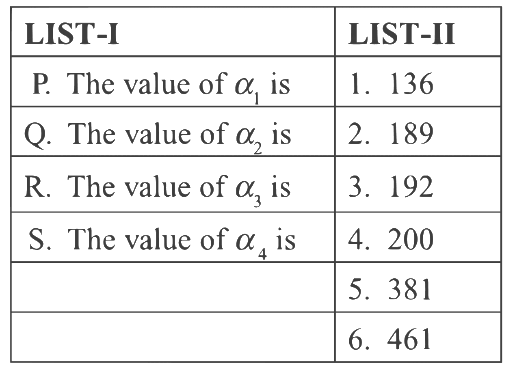
(c) P → 4; Q → 6; R → 5; S → 2
(d) P → 4; Q → 2; R → 3; S → 1 [JEE Advanced 2018 Paper 2]
Ans: (c)
Given 6 boys M1, M2, M3, M4, M5, M6 and 5 girls G1, G2, G3, G4, G5
(i) α1 → Total number of ways of selecting 3 boys and 2 girls from 6 boys and 5 girls.
i.e.,
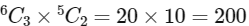
∴ α1 = 200
(ii) α2 → Total number of ways selecting at least 2 member and having equal number of boys and girls i.e.,
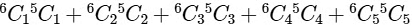
= 30 + 150 + 200 + 75 + 6 = 461
α2 = 461
(iii) α3 → Total number of ways of selecting 5 members in which at least 2 of them girls
i.e.,
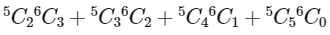
= 200 + 150 + 30 + 1 = 381
α3 = 381
(iv) α4 → Total number of ways of selecting 4 members in which at least two girls such that M1 and G1 are not included together.
G1 is included →
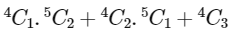
40 + 30 + 4 = 74
M1 is included →
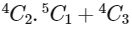= 30 + 4 = 34G1 and M1 both are not included
= 1 + 20 + 60 = 81∴ Total number = 74 + 34 + 81 = 189
α4 = 189
Now, P → 4 ; Q → 6 ; R → 5 ; S → 2
Hence, option (C) is correct.
|
209 videos|443 docs|143 tests
|
|
Dec 22, 2024 Last updated |
|
209 videos|443 docs|143 tests
|
|
Explore Courses for JEE exam
|
|
ppt
,video lectures
,Important questions
,JEE Advanced Previous Year Questions (2018 - 2023): Permutations and Combinations | Mathematics (Maths) for JEE Main & Advanced
,Exam
,mock tests for examination
,Semester Notes
,past year papers
,JEE Advanced Previous Year Questions (2018 - 2023): Permutations and Combinations | Mathematics (Maths) for JEE Main & Advanced
,study material
,Sample Paper
,practice quizzes
,Free
,MCQs
,Viva Questions
,Previous Year Questions with Solutions
,Summary
,Extra Questions
,shortcuts and tricks
,Objective type Questions
,JEE Advanced Previous Year Questions (2018 - 2023): Permutations and Combinations | Mathematics (Maths) for JEE Main & Advanced
;
JEE Advanced Previous Year Questions (2018 - 2023): Permutations and Combinations Free PDF Download
Importance of JEE Advanced Previous Year Questions (2018 - 2023): Permutations and Combinations
JEE Advanced Previous Year Questions (2018 - 2023): Permutations and Combinations Notes
JEE Advanced Previous Year Questions (2018 - 2023): Permutations and Combinations JEE
Study JEE Advanced Previous Year Questions (2018 - 2023): Permutations and Combinations on the App
|
© EduRev
|
Education Revolution
|
|
