JEE Advanced Previous Year Questions (2018 - 2023): Sequences and Series | Mathematics (Maths) for JEE Main & Advanced PDF Download

2023

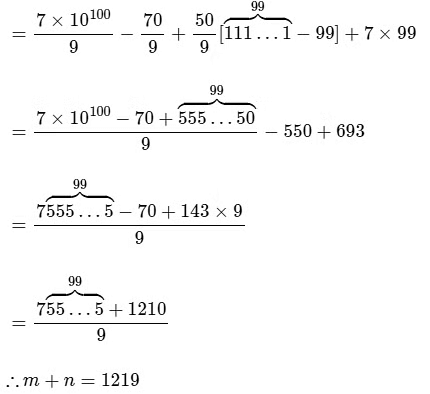
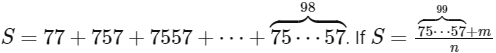Q1: Let  denote the (r + 2) digit number where the first and the last digits are 7 and the remaining r digits are 5 . Consider the sum  , where m and n are natural numbers less than 3000 , then the value of m + n is:                [JEE Advanced 2023 Paper 1]
Ans: 1219

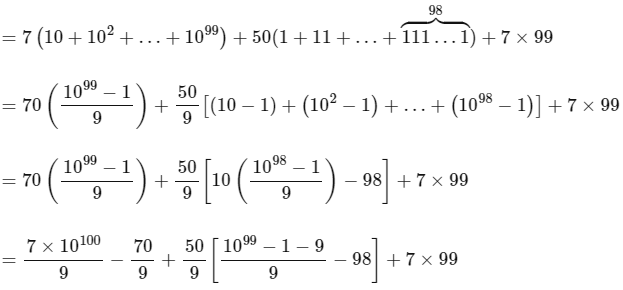
2022

Q1: Let a₁, a₂, a₃,… be an arithmetic progression with a₁ = 7 and common difference 8. Let T₁, T₂, T₃,… be such that T1 = 3 and T_n+1 − T_n = an for n ≥ 1. Then, which of the following is/are TRUE ? 
(a) T₂₀ = 1604
(b)
(c) T₃₀ = 3454
(d) 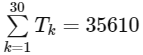                   [JEE Advanced 2022 Paper 1]
Ans: (b) & (c)
Here a_n = 7 + (n - 1)8 and T₁ = 3, a1 = 7, d = 8
Also, T_n+1 = T_n + a_n

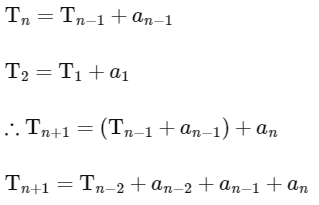
So,

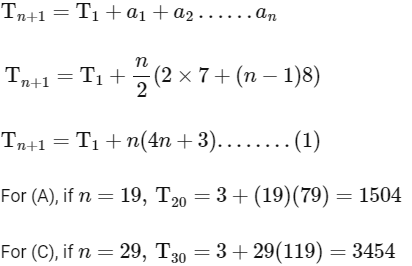
For (B),

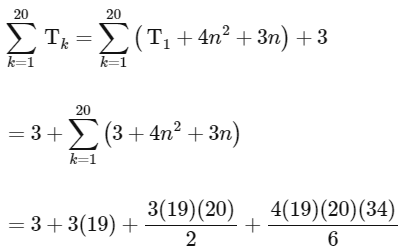
= 3 + 10507
=  10510
Similarly, for (D)

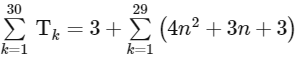
= 35615

Q2: Let l₁, l₂,…,l₁₀₀ be consecutive terms of an arithmetic progression with common difference d₁, and let w₁, w₂,…,w₁₀₀ be consecutive terms of another arithmetic progression with common difference d₂, where d₁d₂ = 10. For each i =1, 2,…,100, let R_i be a rectangle with length l_i, width w_i and area A_i. If A₅₁ − A₅₀ = 1000, then the value of A₁₀₀ − A₉₀ is __________.           [JEE Advanced 2022 Paper 1]
Ans: 18900
Given,
l₁, l₂,…,l₁₀₀ are in A.P with common difference d₁.
So from property of A.P we can say,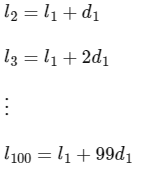

Also given,
w₁, w₂,…,w₁₀₀ are in A.P with common difference d₂. 
∴ From the property of A.P we can say,

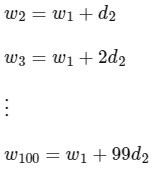
Now, also given,
d₁d₂ = 10
and R_i is a rectangle whose length is l_i and width is w_i and area A_i.
We know, area of rectangle 

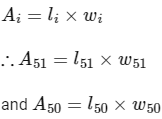
Given,
A₅₁ − A₅₀ = 1000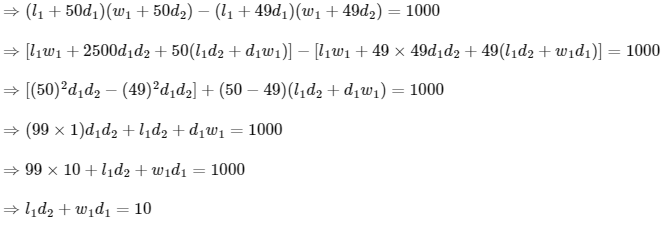

Now, 

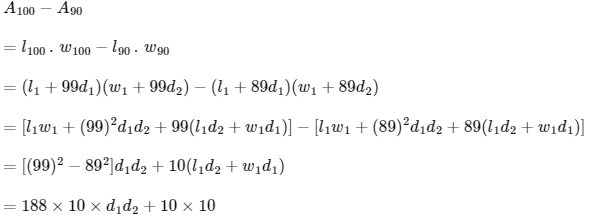
= 1800 x 10 x 10 + 100
= 18800 + 100
= 18900

2020

Q1: Let m be the minimum possible value of 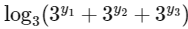, where y₁, y₂, y₃ are real numbers for which y₁+ y₂ + y₃ = 9. Let M be the maximum possible value of 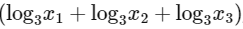, where x₁ , x₂, x₃ are positive real numbers for which x₁ + x₂ + x₃ = 9. Then the value of  is _________     [JEE Advanced 2020 Paper 1]
Ans: 8
For real numbers y₁, y₂, y₃, the quantities 3^y1, 3^y2 and 3^y3 are positive real numbers, so according to the AM-GM inequality, we have 

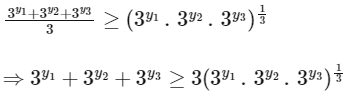
On applying logarithm with base '3', we get

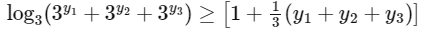
= 1 + 3
= 4
∴ m = 4
Now, for positive real numbers x₁, x₂ and x₃ according to AM-GM inequality, we have

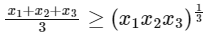
On applying logarithm with base '3', we get

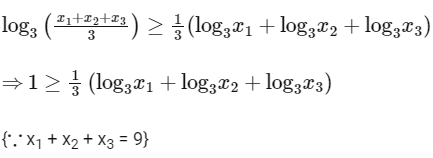
∴ M = 3
Now,
=
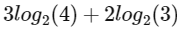
= 6 + 2
= 8

Q2: Let a₁, a₂, a₃, .... be a sequence of positive integers in arithmetic progression with common difference 2. Also, let b₁, b₂, b₃, .... be a sequence of positive integers in geometric progression with common ratio 2. If a₁ = b₁ = c, then the number of all possible values of c, for which the equality 2(a₁ + a₂ + ... + a_n) = b₁ + b₂ + ... + b_n holds for some positive integer n, is ____                [JEE Advanced 2020 Paper 1]
Ans: 1
Given arithmetic progression of positive integers terms a₁, a₂, a₃, ..... having common difference '2' and geometric progression of positive integers terms b₁, b₂, b₃, .... having common ratio '2' with a₁ = b₁ = c, such that:
2(a₁ + a₂ + a₃ + ... + a_n) = b₁ + b₂ + b₃ + ... + b_n 

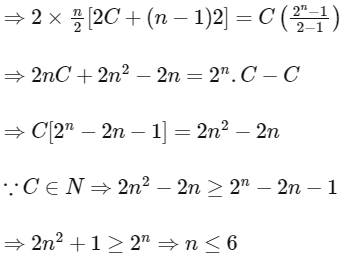
and, also C > 0 ⇒ n > 2
∴ The possible values of n are 3, 4, 5, 6 

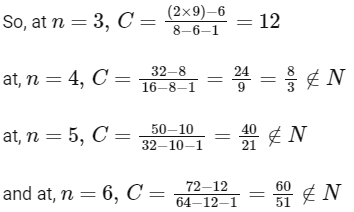
∴ The required value of C = 12 for n = 3
so number of possible value of C is 1 

2019

Q1: Let AP(a; d) denote the set of all the terms of an infinite arithmetic progression with first term a and common difference d > 0. If 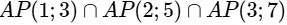 = AP(a ; d), then a + d equals ________      [JEE Advanced 2019 Paper 1]
Ans: 157
Given that, AP(a ; d) denote the set of all the terms of an infinite arithmetic progression with first term 'a' and common difference d > 0.
Now, let m^th term of first progression

and nth term of progression

and r^th term of third progression

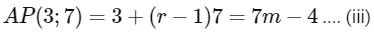 are equal.
Then,  3m - 2 = 5n - 3 = 7r - 4
Now, for
the common terms of first and second progressions,
⇒ n = 2, 5, 11, ...
and the common terms of second and the third progressions, 

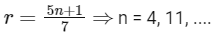
Now, the first common term of first, second and third progressions (when n = 11), so
a = 2 + (11 - 1)5 = 52
and d = LCM (3, 5, 7) = 105
So, 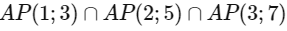 = AP(52; 105)
So, a = 52 and d = 105
⇒ a + d = 157.00 

2018

Q1: Let X be the set consisting of the first 2018 terms of the arithmetic progression 1, 6, 11, ...., and Y be the set consisting of the first 2018 terms of the arithmetic progression 9, 16, 23, .... . Then, the number of elements in the set X ∪ Y is _____.             [JEE Advanced 2018 Paper 1]
Ans: 3748
Here, X = {1, 6, 11, ....., 10086}
[∵ a_n = a + (n − 1)d]
and Y = {9, 16, 23, ..., 14128}
X ∩ Y = {16, 51, 86, ...}
t_n of X ∩ Y is less than or equal to 10086
∴ t_n = 16 + (n − 1) 35 ≤ 10086
⇒ n ≤ 288.7
∴ n = 288
∵ n(X ∩ Y) = n(X) + n(Y) − n(X ∩ Y)
∴ n(X ∩ Y) = 2018 + 2018 − 288 
= 3748