JEE Main Previous Year Questions (2019): Permutations and Combinations | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q1: A group of students comprises of 5 boys and n girls. If the number of ways, in which a team of 3 students can randomly be selected from this group such that there is at least one boy and at least one girl in each team, is 1750, then n is equal to :
(a) 24
(b) 25
(c) 27
(d) 28
Ans: (b)
Given that 5 Boy, n girls.
(1B, 2G) + (2B, 1G)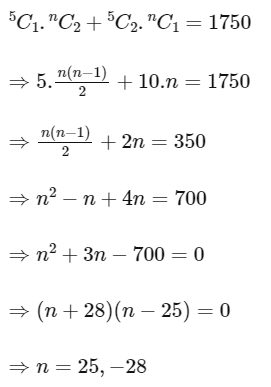
Q2: The number of ways of choosing 10 objects out of 31 objects of which 10 are identical and the remaining 21 are distinct, is :
(a) 220 - 1
(b) 220
(c) 220 + 1
(d) 221
Ans: (b)
Q3: Suppose that 20 pillars of the same height have been erected along the boundary of a circular stadium. If the top of each pillar has been connected by beams with the top of all its non-adjacent pillars, then the total number of beams is :
(a) 180
(b) 210
(c) 170
(d) 190
Ans: (c)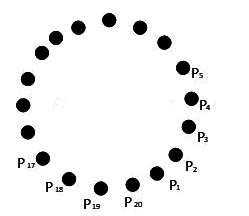 Any two non-adjacent pillers are joined by beams
Any two non-adjacent pillers are joined by beams
∴ number of beams = number of diagonals = 20C2 - 20 = 170
Q4: The number of 6 digit numbers that can be formed using the digits 0, 1, 2, 5, 7 and 9 which are divisible by 11 and no digit is repeated is :
(a) 36
(b) 60
(c) 72
(d) 48
Ans: (b)
digit 0, 1, 2, 5, 7, 9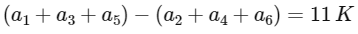
so (1, 2, 9) (0, 5, 7)
Now number of ways to arranging them
= 3! × 3! + 3! × 2 × 2
= 6 × 6 + 6 × 4
= 6 × 10
= 60
Q5: A committee of 11 members is to be formed from 8 males and 5 females. If m is the number of ways the committee is formed with at least 6 males and n is the number of ways the committee is formed with at least 3 females, then :
(a) n = m – 8
(b) m = n = 78
(c) m + n = 68
(d) m = n = 68
Ans: (b)
At least 6 males means in the committee there can be 6 males or 7 males or 8 males.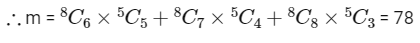
At least 3 females means in the committee there can be 3 females or 4 females or 5 females.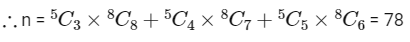
So, m = n = 78
Q6: The number of four-digit numbers strictly greater than 4321 that can be formed using the digits 0,1,2,3,4,5 (repetition of digits is allowed) is :
(a) 306
(b) 288
(c) 310
(d) 360
Ans: (c)
Case1 : When first digit is 5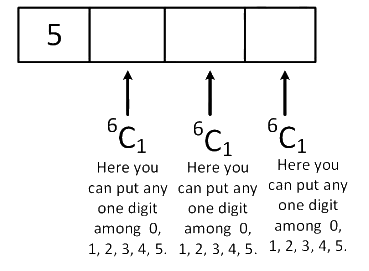 So total possible 4 digit numbers when first digit is 5
So total possible 4 digit numbers when first digit is 5
Case 2: When first digit is 4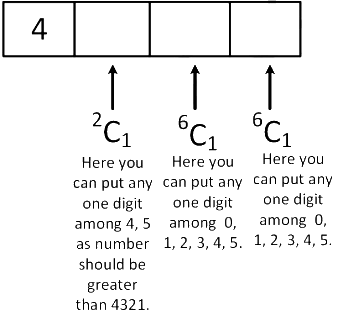 So total possible 4 digit numbers when first digit is 4
So total possible 4 digit numbers when first digit is 4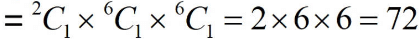
Case 3: When first two digits are 4 and 3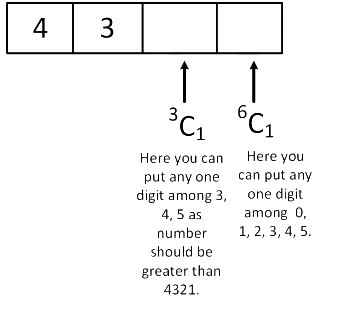 So total possible 4 digit numbers when first two digits are 4 and 3
So total possible 4 digit numbers when first two digits are 4 and 3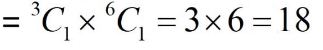
Case 4: When first three digits are 4, 3 and 2.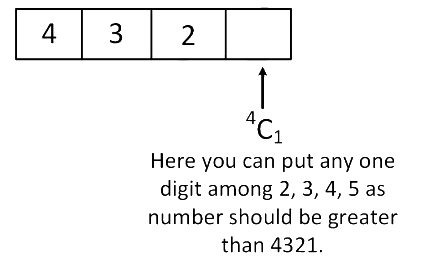 So total possible 4 digit numbers when first two digits are 4 and 3
So total possible 4 digit numbers when first two digits are 4 and 3
= 4C1 = 4
So total 4 digit numbers possibe = 216 + 72 + 18 + 4 = 310
Q7: All possible numbers are formed using the digits 1, 1, 2, 2, 2, 2, 3, 4, 4 taken all at a time. The number of such numbers in which the odd digits occupy even places is :
(a) 175
(b) 162
(c) 160
(d) 180
Ans: (d)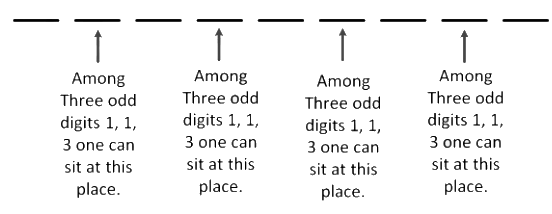 For those three odd digit numbers 1, 1, 3 we can choose any three positions out of the four even positions.
For those three odd digit numbers 1, 1, 3 we can choose any three positions out of the four even positions.
∴ No of ways we can choose 3 positions out of the 4 positions = 4C3
After choosing those three positions, number of ways we can arrange three odd digit numbers 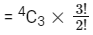
Then the remaining 6 digits can be arrange 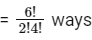
∴ Total number of 9 digit numbers 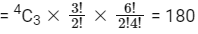
Q8: There are m men and two women participating in a chess tournament. Each participant plays two games with every other participant. If the number of games played by the men between themselves exceeds the number of games played between the men and the women by 84, then the value of m is :
(a) 12
(b) 9
(c) 7
(d) 11
Ans: (a)
Let m-men, 2-women
mC2 × 2 = mC1 2C1 . 2 + 84
m2 − 5m − 84 = 0 ⇒ (m − 12) (m + 7) = 0
m = 12
Q9: Consider three boxes, each containing, 10 balls labelled 1, 2, … , 10. Suppose one ball is randomly drawn from each of the boxes. Denote by ni, the label of the ball drawn from the ith box, (i = 1, 2, 3). Then, the number of ways in which the balls can be chosen such that n1 < n2 < n3 is :
(a) 164
(b) 240
(c) 82
(d) 120
Ans: (d)
Number of ways = 10C3 = 120
Q10: If 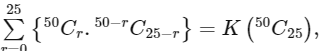 then K is equal to :
then K is equal to :
(a) 224
(b) 225 - 1
(c) 225
(d) (25)2
Ans: (c)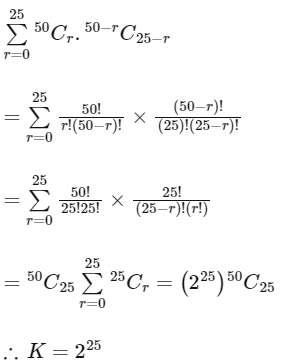
Q11: Let S be the set of all triangles in the xy-plane, each having one vertex at the origin and the other two vertices lie on coordinate axes with integral coordinates. If each triangle in S has area 50 sq. units, then the number of elements in the set S is :
(a) 9
(b) 18
(c) 36
(d) 32
Ans: (c)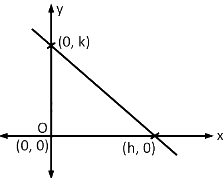 Area = 1/2 h. k = 50
Area = 1/2 h. k = 50
h. k = 100
h. k = 22 . 52
Total divisors
= (2 + 1) (2 + 1) = 9
if h > 0, k > 0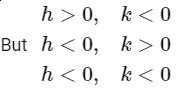
all are possible so that total no. of positive case
9 + 9 + 9 + 9 = 36
Q12: The number of natural numbers less than 7,000 which can be formed by using the digits 0, 1, 3, 7, 9 (repitition of digits allowed) is equal to :
(a) 374
(b) 372
(c) 375
(d) 250
Ans: (a)
Total no 1 digit numbers possible = 4 (allowed digits 1, 3, 7, 9)
Total no 2 digit numbers possible = 4×5 = 20
Total no 3 digit numbers possible = 4×5×5 = 100
Total no 4 digit numbers possible = 2×5×5×5 = 250
So the number of natural numbers less than 7,000 possible are
= 4 + 20 + 100 + 250 = 374
Q13: Consider a class of 5 girls and 7 boys. The number of different teams consisting of 2 girls and 3 boys that can be formed from this class, if there are two specific boys A and B, who refuse to be the members of the same team, is:
(a) 500
(b) 350
(c) 200
(d) 300
Ans: (d)
From 5 girls 2 girls can be selected
= 5C2 ways
From 7 boys 3 boys can be selected
= 7C3 way
∴ Total number of ways we can select 2 girls and 3 boys
= 5C2 × 7C3 ways
When two boys A and B are chosen in a team then one more boy will be chosen from remaining 5 boys.
So, no of ways 3 boys can be chosen when A and B should must be chosen = 5C1 ways
∴ Total number of ways a team of 2 girl and 3 boys can be made where boy A and B must be in the team = 5C1 × 5C2 ways
∴ Required number of ways
= Total number of ways − when A and B are always included.
= 5C2 × 7C3 − 5C1 × 5C2
= 300
|
446 docs|930 tests
|

|
Explore Courses for JEE exam
|

|
















