JEE Main Previous Year Questions (2025): Gravitation | Chapter-wise Tests for JEE Main & Advanced PDF Download
[JEE Mains MCQs]
Q1: Two planets have masses M and 16 M and their radii are a and 2a , respectively. The separation between the centres of the planets is 10a. A body of mass m is fired from the surface of the larger planet towards the smaller planet along the line joining their centres. For the body to be able to reach at the surface of smaller planet, the minimum firing speed needed is:
(a) 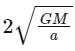
(b) 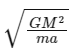
(c) 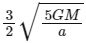
(d) 
Ans: (c)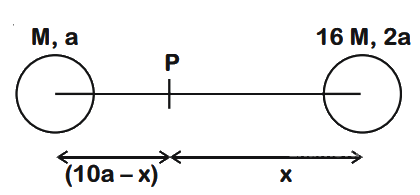 Let at point P, net gravitational force = 0
Let at point P, net gravitational force = 0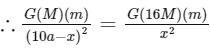
⇒ x = 8a
By Conservation of Mechanical Energy,
Ui + Ki = Uf + Kf 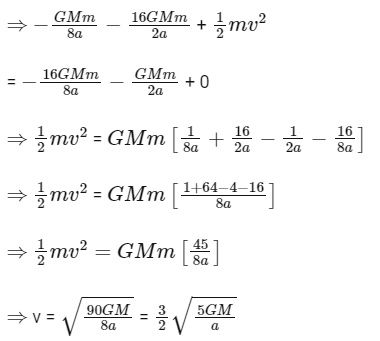
Q2: A satellite is in an elliptical orbit around a planet P. It is observed that the velocity of the satellite when it is farthest from the planet is 6 times less than that when it is closest to the planet. The ratio of distances between the satellite and the planet at closest and farthest points is:
(a) 1 : 2
(b) 1 : 3
(c) 1 : 6
(d) 3 : 4
Ans: (c)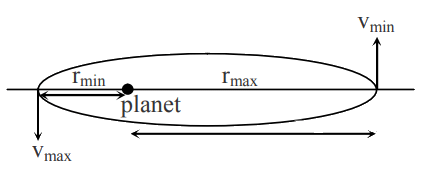 By angular momentum conservation
By angular momentum conservation
Li = Lf
rminvmax = rmaxvmin .....(i)
Given, vmax = 6vmin
From equation (i), 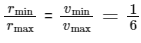
Q3: The acceleration due to gravity on the earth’s surface at the poles is g and angular velocity of the earth about the axis passing through the pole is ω. An object is weighed at the equator and at a height h above the poles by using a spring balance. If the weights are found to be same, then h is (h << R, where R is the radius of the earth)
(a) 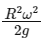
(b) 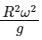
(c) 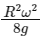
(d) 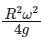
Ans: (a)
At equator, g1 = g - Rω2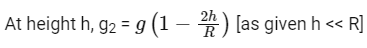
∵ Weight same at poles and at h (so g1 = g2)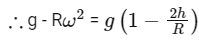
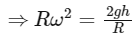
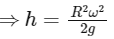
Q4: The value of the acceleration due to gravity is g1 at a height h = R/2 (R = radius of the earth) from the surface of the earth. It is again equal to g1 at a depth d below the surface of the earth. The ratio (d/R) equals:
(a) 5/9
(b) 1/9
(c) 7/9
(d) 4/9
Ans: (a)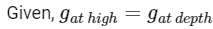
Q5: A body is moving in a low circular orbit about a planet of mass M and radius R. The radius of the orbit can be taken to be R itself. Then the ratio of the speed of this body in the orbit to the escape velocity from the planet is:
(a) 2
(b) 1
(c) √2
(d) 1/√2
Ans: (d)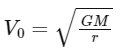
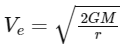
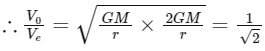
Q6: On the x-axis and at a distance x from the origin, the gravitational field due a mass distribution is given by 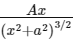 in the x-direction. The magnitude of gravitational potential on the x-axis at a distance x, taking its value to be zero at infinity, is:
in the x-direction. The magnitude of gravitational potential on the x-axis at a distance x, taking its value to be zero at infinity, is:
(a) A(x2 + a2)3/2
(b) A(x2 + a2)1/2
(c) 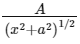
(d) 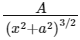
Ans: (c)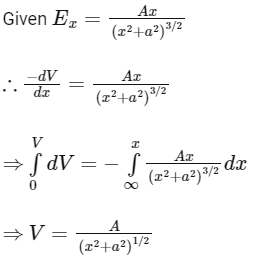
Q7: The mass density of a planet of radius R varies with the distance r from its centre as 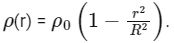
Then the gravitational field is maximum at:
(a) 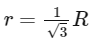
(b) r = R
(c) 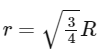
(d) 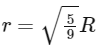
Ans: (d)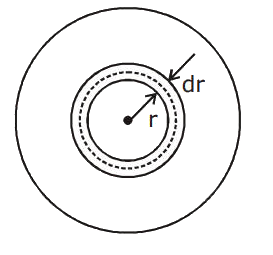 dm = ρdv
dm = ρdv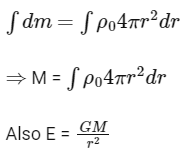
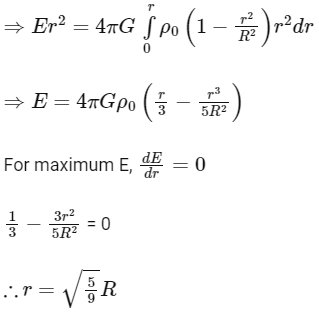
Q8: A satellite is moving in a low nearly circular orbit around the earth. Its radius is roughly equal to that of the earth’s radius Re . By firing rockets attached to it, its speed is instantaneously increased in the direction of its motion so that it become 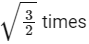 larger. Due to this the farthest distance from the centre of the earth that the satellite reaches is R. Value of R is:
larger. Due to this the farthest distance from the centre of the earth that the satellite reaches is R. Value of R is:
(a) 2Re
(b) 3Re
(c) 4Re
(d) 2.5Re
Ans: (b)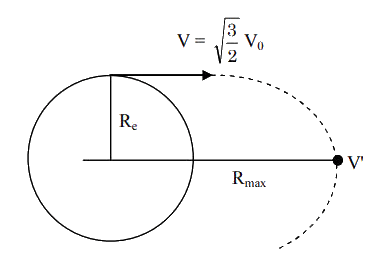
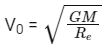
Applying Conservation of Angular Momentum,
mVRe = mV'R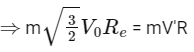
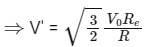
Applying Conservation of Energy,
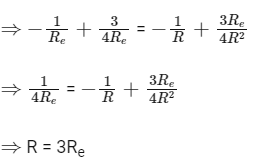
Q9: The height ‘h’ at which the weight of a body will be the same as that at the same depth ‘h’ from the surface of the earth is (Radius of the earth is R and effect of the rotation of the earth is neglected)
(a) R/2
(b) 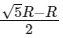
(c) 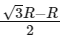
(d) 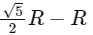
Ans: (b)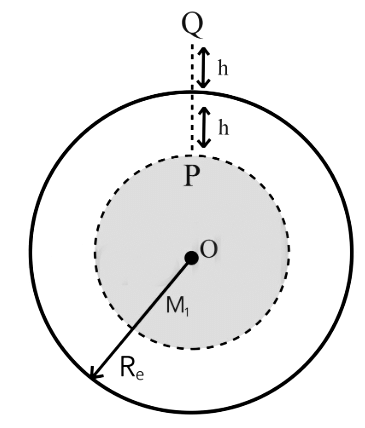 M = mass of earth
M = mass of earth
M1 = mass of shaded portion
Re = Radius of earth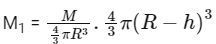
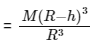
Given, Weight of body is same at P and Q
∴ mgP = mgQ
⇒ gP = gQ 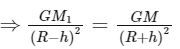

⇒ (R – h) (R + h)2 = R3
⇒ R3 – hR2 + h2R – h3 + 2R2h – 2Rh2 = R3
⇒ R2h – Rh2 – h3 = 0
⇒ R2 – Rh – h2 = 0
⇒ h2 + Rh – R2 = 0 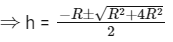
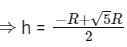
Q10: The mass density of a spherical galaxy varies as K/r over a large distance ‘r’ from its centre. In that region, a small star is in a circular orbit of radius R. Then the period of revolution, T depends on R as:
(a) T2 ∝ R
(b) T2 ∝ R3
(c) T ∝ R
(d) 
Ans: (a)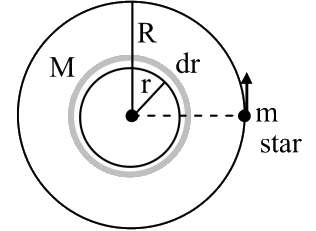 dm = ρdv
dm = ρdv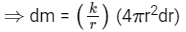
⇒ dm = 4πkrdr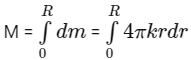
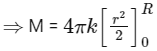
⇒ M = 2 π kR2
For circular motion gravitational force will provide required centripetal force.
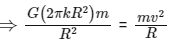
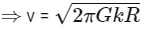
Time period, 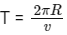
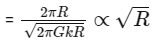
⇒ T2 ∝ R
Q11: Planet A has mass M and radius R. Planet B has half the mass and half the radius of Planet A. If the escape velocities from the Planets A and B are vA and vB, respectively, then vA/vB = n/4. The value of n is:
(a) 1
(b) 2
(c) 4
(d) 3
Ans: (c)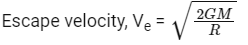
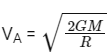
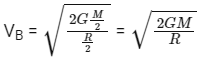
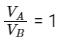
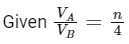
∴ n/4 = 1
⇒ n = 4
Q12: A body A of mass m is moving in a circular orbit of radius R about a planet. Another body B of mass m/2 collides with A with a velocity which is half  the instantaneous velocity
the instantaneous velocity 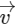 of A. The collision is completely inelastic. Then, the combined body:
of A. The collision is completely inelastic. Then, the combined body:
(a) Starts moving in an elliptical orbit around the planet.
(b) Falls vertically downwards towards the planet
(c) Escapes from the Planet's Gravitational field.
(d) Continues to move in a circular orbit
Ans: (a)
Orbital speed for of A is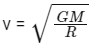
After collision, let the combined mass moves with speed v1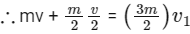
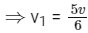
Since after collision, the speed is not equal to orbital speed at that point. So motion cannot be circular. Since velocity will remain tangential, so it cannot fall vertically towards the planet. Their speed after collision is less than escape speed √2v , so they cannot escape gravitational field. So their motion will be elliptical around the planet.
Q13: Consider two solid spheres of radii R1 = 1m, R2 = 2m and masses M1 and M2, respectively. The gravitational field due to sphere (1) and (2) are shown. The value of M1/M2 is: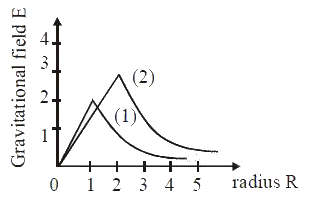 (a) 2/3
(a) 2/3
(b) 1/6
(c) 1/2
(d) 1/3
Ans: (b)
Gravitational field on the surface of a solid sphere
By the graph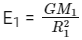
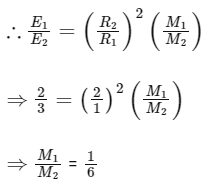
Q14: A box weight 196 N on a spring balance at the north pole. Its weight recorded on the same balance if it is shifted to the equator is close to (Take g = 10 ms–2 at the north pole and the radius of the earth = 6400 km):
(a) 194.32 N
(b) 195.66 N
(c) 195.32 N
(d) 194.66 N
Ans: (c)
At equator, weight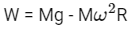
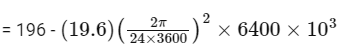
= 195.32 N
Q15: A satellite of mass m is launched vertically upwards with an initial speed u from the surface of the earth. After it reaches height R (R = radius of the earth), it ejects a rocket of mass m/10 so that subsequently the satellite moves in a circular orbit. The kinetic energy of the rocket is (G is the gravitational constant; M is the mass of the earth):
(a) 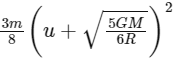
(b) 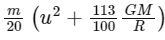
(c) 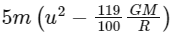
(d) 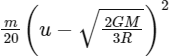
Ans: (c)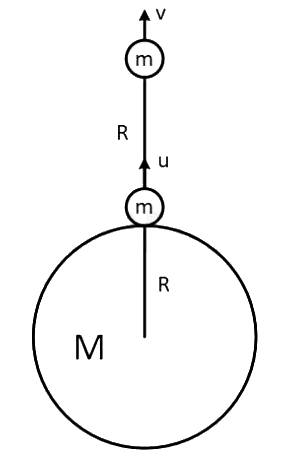 Using energy conservation
Using energy conservation
Ki + Ui = Kf + Uf 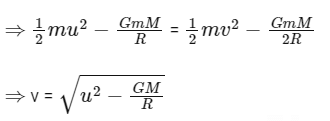
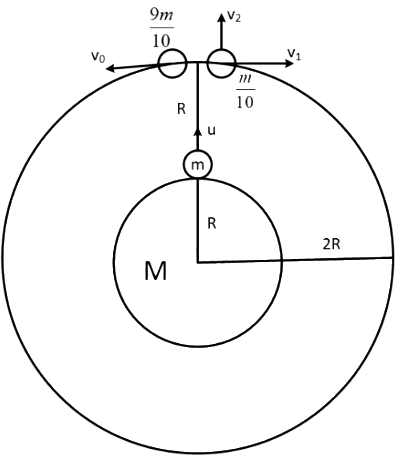 After ejecting a rocket of mass m/10 the remaining part of mass 9m/10 will rotate the earth with orbital velocity v0.
After ejecting a rocket of mass m/10 the remaining part of mass 9m/10 will rotate the earth with orbital velocity v0.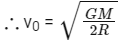
Applying momentum conservation along radial direction,
Before firing rocket momentum of satelite in radial direction = mv
And after firing rocket momentum of satelite in radial direction = 0 and momentum of rocket in radial direction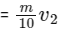
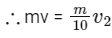
⇒ v2 = 10v
Now applying momentum conservation along tangential direction we get,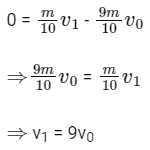
∴ Total Kinetic Energy of rocket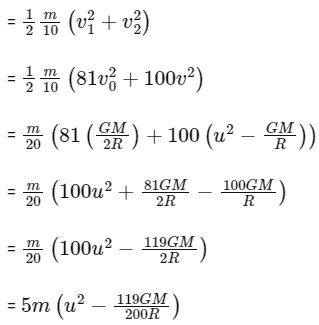
[JEE Mains Numericals]
Q16: A ball is dropped from the top of a 100 m high tower on a planet. In the last 1/2 s before hitting the ground, it covers a distance of 19 m. Acceleration due to gravity (in ms–2) near the surface on that planet is _____.
Ans: 8
Let time to travel 81 m is t sec.
Time to travel 100 m is 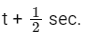
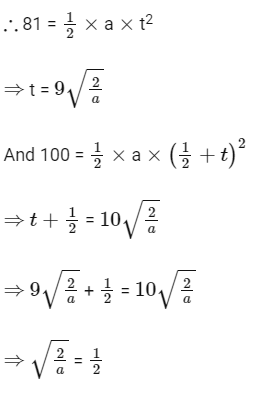
⇒ a = 8 m/s2
Q17: An asteroid is moving directly towards the centre of the earth. When at a distance of 10R (R is the radius of the earth) from the earths centre, it has a speed of 12 km/s. Neglecting the effect of earths atmosphere, what will be the speed of the asteroid when it hits the surface of the earth (escape velocity from the earth is 11.2 km/s) ? Give your answer to the nearest integer in kilometer/s _____.
Ans: 16
U1 + K1 = U2 + K2 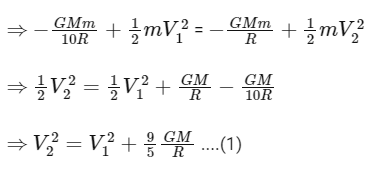
Given escape velocity Ve = 11.2 km/s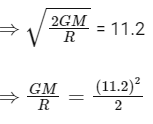
So from (1)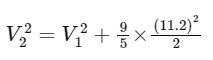
= (12)2 + 112.896
⇒ V2 = 16 km/s
|
446 docs|929 tests
|
FAQs on JEE Main Previous Year Questions (2025): Gravitation - Chapter-wise Tests for JEE Main & Advanced
| 1. What is the formula to calculate the gravitational force between two objects? |  |
| 2. How does the gravitational force change with the increase in distance between two objects? |  |
| 3. How does the gravitational force change with the increase in mass of one of the objects? |  |
| 4. What is escape velocity? |  |
| 5. How does the gravitational force change at the surface of the Earth compared to the height above the surface? |  |















