JEE Main Previous Year Questions (2022): Gravitation | Chapter-wise Tests for JEE Main & Advanced PDF Download

[JEE Mains MCQs]

Q1: An object of mass 1 kg is taken to a height from the surface of earth which is equal to three times the radius of earth. The gain in potential energy of the object will be [If, g = 10 ms⁻² and radius of earth = 6400 km]
(a) 48 MJ
(b) 24 MJ
(c) 36 MJ
(d) 12 MJ
Ans: (a)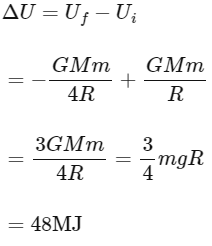


Q2: If the radius of earth shrinks by 2 % while its mass remains same. The acceleration due to gravity on the earth's surface will approximately :
(a) decrease by 2 %
(b) decrease by 4 %
(c) increase by 2 %
(d)  increase by 4 %
Ans: (d)
The acceleration due to gravity (g) on the surface of a planet is given by the formula:

where:
G is the gravitational constant,
M is the mass of the planet,
R is the radius of the planet.
If the radius of the Earth shrinks by 2% but its mass remains the same, the new acceleration due to gravity (g') will be: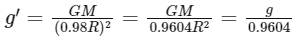

This implies that g' is approximately 1.0412 times g, or an increase of approximately 4.12%.
Therefore, the acceleration due to gravity on the Earth's surface will approximately increase by 4%.

Q3: A body of mass m is projected with velocity λv_e in vertically upward direction from the surface of the earth into space. It is given that v_e is escape velocity and λ < 1. If air resistance is considered to be negligible, then the maximum height from the centre of earth, to which the body can go, will be :
(R : radius of earth)
(a)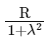
(b)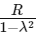
(c)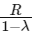
(d)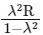
Ans: (b)
Using energy conservation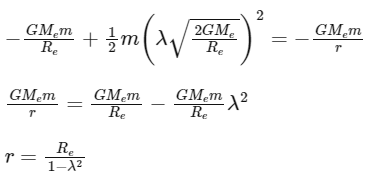


Q4: Two satellites A and B , having masses in the ratio 4 : 3 , are revolving in circular orbits of radii 3r and 4r respectively around the earth. The ratio of total mechanical energy of A to B is :
(a) 9 : 16
(b) 16 : 9
(c) 1 : 1
(d) 4 : 3
Ans: (b)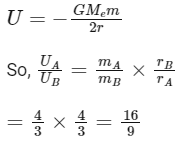


Q5: A body is projected vertically upwards from the surface of earth with a velocity equal to one third of escape velocity. The maximum height attained by the body will be :
(Take radius of earth = 6400 km and g = 10 ms⁻²)
(a) 800 km
(b)1600 km
(c) 2133 km
(d) 4800 km
Ans: (a)
Applying conservation of energy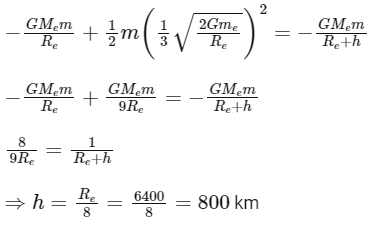


Q6: The percentage decrease in the weight of a rocket, when taken to a height of 32 km above the surface of earth will, be : (Radius of earth = 6400 km)
(a) 1%
(b) 3%
(c) 4%
(d) 0.5%
Ans: (a)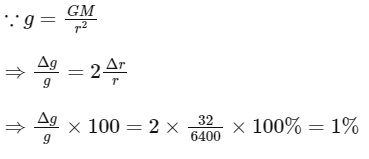

⇒ % decrease in weight = 1%

Q7: The length of a simple pendulum at a height h = 2R from earth surface will be:
(Given R = Radius of earth and acceleration due to gravity at the surface of earth, g = π² ms^-2)
(a) 2/9 m
(b) 4/9 m
(c) 8/9 m
(d) 1/9 m
Ans: (d)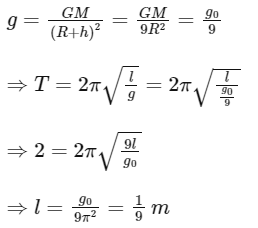


Q8: An object is taken to a height above the surface of earth at a distance 5/4 R from the centre of the earth. Where radius of earth, R = 6400 km. The percentage decrease in the weight of the object will be:
(a) 36%
(b) 50%
(c) 64%
(d) 25%
Ans: (a)
The weight of an object at a distance d from the center of the Earth is given by: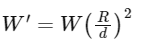

where:
W' is the weight at distance d,
W is the weight at the Earth's surface,
R is the radius of the Earth,
d is the distance from the center of the Earth.
In this problem, we are asked to find the percentage decrease in weight, which can be calculated by: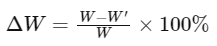

where ΔW is the percentage change in weight. Substituting the weight formula into the percentage change formula gives: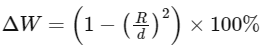

The radius of the Earth R is 6400 km and the distance d from the center of the Earth is given as 5/4 R. Substituting these values into the equation gives: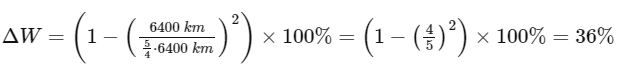

Therefore, the percentage decrease in the weight of the object when taken to a height of 1/4 R above the surface of the Earth is 36%.

Q9: Three identical particles A, B and C of mass 100 kg each are placed in a straight line with AB = BC = 13 m. The gravitational force on a fourth particle P of the same mass is F, when placed at a distance 13 m from the particle B on the perpendicular bisector of the line AC. The value of F will be approximately:
(a) 21 G
(b) 100 G
(c) 59 G
(d) 42 G
Ans: (b)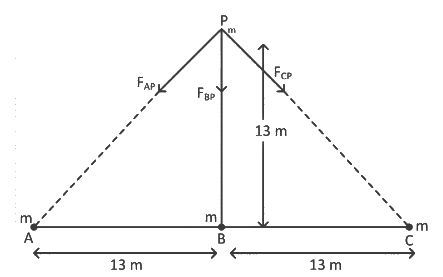
m = 100 kg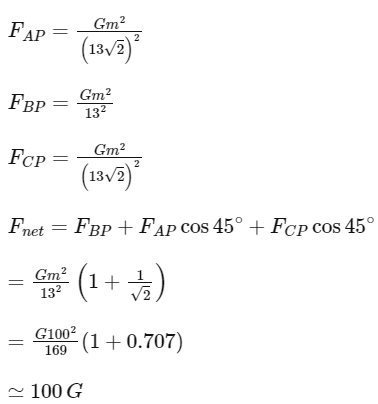


Q10: The radii of two planets A and B are in the ratio 2 : 3. Their densities are 3ρ and 5ρ respectively. The ratio of their acceleration due to gravity is :
(a) 9 : 4
(b) 9 : 8
(c) 9 : 10
(d) 2 : 5
Ans: (d)
Given,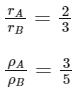

We know,
Acceleration due to gravity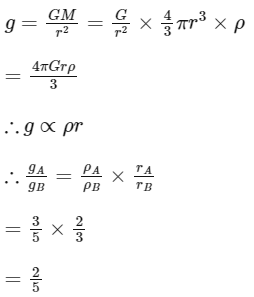


Q11: The time period of a satellite revolving around earth in a given orbit is 7 hours. If the radius of orbit is increased to three times its previous value, then approximate new time period of the satellite will be
(a) 40 hours
(b) 36 hours
(c) 30 hours
(d) 25 hours
Ans: (b)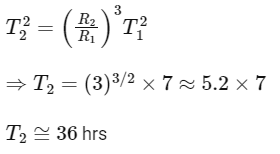


Q12: The escape velocity of a body on a planet 'A' is 12 kms⁻¹. The escape velocity of the body on another planet 'B', whose density is four times and radius is half of the planet 'A', is :
(a) 12 kms⁻¹ 
(b) 24 kms⁻¹ 
(c) 36 kms⁻¹ 
(d) 6 kms⁻¹
Ans: (a)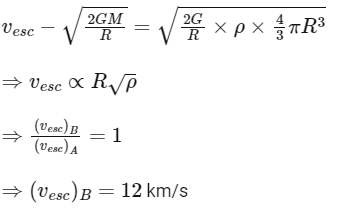


Q13: Water falls from a 40 m high dam at the rate of 9 × 10⁴ kg per hour. Fifty percentage of gravitational potential energy can be converted into electrical energy. Using this hydroelectric energy number of 100 W lamps, that can be lit, is : (Take g = 10 ms⁻²)
(a) 25
(b) 50
(c) 100
(d) 18
Ans: (b)
Total gravitational PE of water per second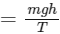

50% of this energy can be converted into electrical energy so total electrical energy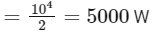

So total bulbs lit can be

Q14: Two objects of equal masses placed at certain distance from each other attracts each other with a force of F. If one-third mass of one object is transferred to the other object, then the new force will be : (a) 2/9 F
(b) 16/9 F
(c) 8/9 F
(d) F
Ans: (c)
Let the masses are m and distance between them is l, then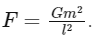

When 1/3rd mass is transferred to the other then masses will be 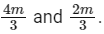 so new force will be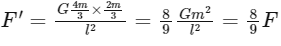


Q15: Two planets A and B of equal mass are having their period of revolutions T_A and T_B such that T_A = 2T_B. These planets are revolving in the circular orbits of radii rA and rB respectively. Which out of the following would be the correct relationship of their orbits?
(a)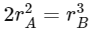
(b)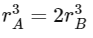
(c)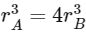
(d)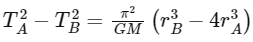
Ans: (c)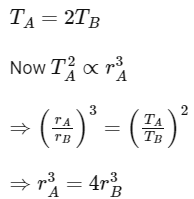


Q16: The distance of the Sun from earth is 1.5 × 10¹¹ m and its angular diameter is (2000) s when observed from the earth. The diameter of the Sun will be:
(a) 2.45 × 10¹⁰ m
(b) 1.45 × 10¹⁰ m
(c) 1.45 × 10⁹ m
(d) 0.14 × 10⁹ m
Ans: (c)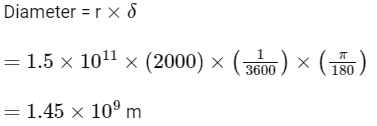


Q17: Four spheres each of mass m from a square of side d (as shown in figure). A fifth sphere of mass M is situated at the centre of square. The total gravitational potential energy of the system is: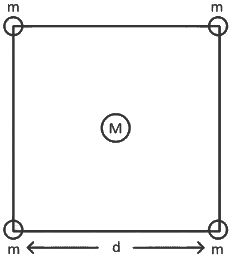
(a)
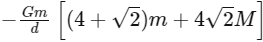
(b)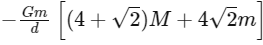
(c)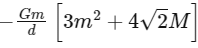
(d)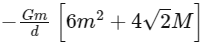
Ans: (a)
Total gravitational potential energy


Q18: Given below are two statements:
Statement I : The law of gravitation holds good for any pair of bodies in the universe.
Statement II : The weight of any person becomes zero when the person is at the centre of the earth.
In the light of the above statements, choose the correct answer from the options given below.
(a) Both Statement I and Statement II are true
(b) Both Statement I and Statement II are false
(c) Statement I is true but Statement II is false
(d) Statement I is false but Statement II is true
Ans: (a)
Statement I is true. Newton's law of universal gravitation states that every particle of matter in the universe attracts every other particle with a force that is directly proportional to the product of the masses of the particles and inversely proportional to the square of the distance between their centers. This law applies to any pair of bodies in the universe.
Statement II is also true. The weight of an object is the force of gravity acting on it. If a person were at the center of the Earth, the gravitational pull from all the surrounding mass of the Earth would cancel out, resulting in zero net gravitational force and therefore zero weight.
Therefore, Option A: Both Statement I and Statement II are true, is the correct answer.

Q19: Given below are two statements : One is labelled as Assertion A and the other is labelled as Reason R.
Assertion A: If we move from poles to equator, the direction of acceleration due to gravity of earth always points towards the center of earth without any variation in its magnitude.
Reason R: At equator, the direction of acceleration due to the gravity is towards the center of earth.
In the light of above statements, choose the correct answer from the options given below:
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is NOT the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Ans: (d)
Assertion A is false. While the direction of acceleration due to gravity does always point towards the center of the Earth, its magnitude actually varies from the poles to the equator. This is due to the Earth's rotation and the fact that Earth is not a perfect sphere but an oblate spheroid, meaning it's slightly flattened at the poles and bulging at the equator.
Reason R is true. At the equator, the direction of acceleration due to gravity is towards the center of the Earth.

Q20: The variation of acceleration due to gravity (g) with distance (r) from the center of the earth is correctly represented by:
(Given R = radius of earth)
(a)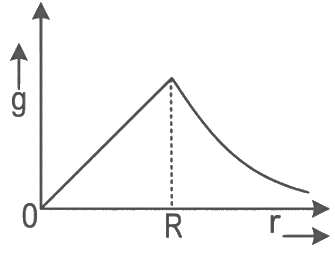

(b)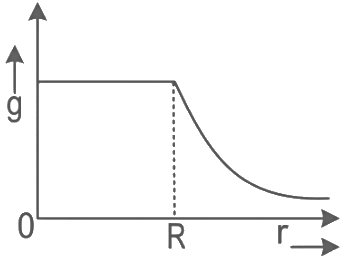

(c)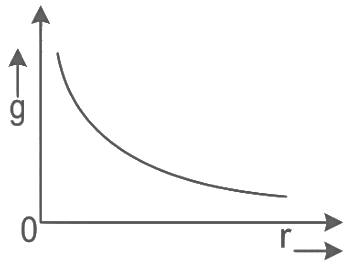

(d)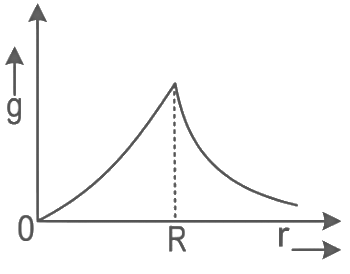

Ans: (a)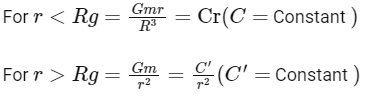

For the above equations the best suited graph is as given in option (A)

Q21: The height of any point P above the surface of earth is equal to diameter of earth. The value of acceleration due to gravity at point P will be : (Given g = acceleration due to gravity at the surface of earth). 
(a) g/2 
(b) g/4 
(c) g/3 
(d) g/9
Ans: (d)
The acceleration due to gravity (g) at a distance (r) from the center of a planet is given by: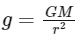

where:
G is the gravitational constant,
M is the mass of the planet,
r is the distance from the center of the planet.
If the height h of a point P above the surface of the Earth is equal to the diameter of the Earth, then the distance r from the center of the Earth to the point P is 3 times the radius of the Earth. Substituting this into the equation for g gives: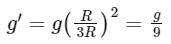

where:
g' is the acceleration due to gravity at the point P,
R is the radius of the Earth.
Therefore, the value of acceleration due to gravity at point P is g/9.

Q22: The distance between Sun and Earth is R. The duration of year if the distance between Sun and Earth becomes 3R will be:
(a) √3 years
(b) 3 years
(c) 9 years
(d) 3√3 years
Ans: (d)
We know that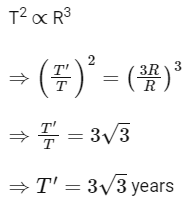


Q23: The approximate height from the surface of earth at which the weight of the body becomes 1/3 of its weight on the surface of earth is:
[Radius of earth R = 6400 km and √3 = 1.732]
(a) 3840 km
(b) 4685 km
(c) 2133 km
(d) 4267 km
Ans: (b)
According to the given information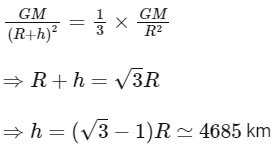

[JEE Mains Numericals]

Q24: If the acceleration due to gravity experienced by a point mass at a height h above the surface of earth is same as that of the acceleration due to gravity at a depth αh (h << R_e) from the earth surface. The value of α will be _________. (use R_e = 64 00 km)
Ans: 2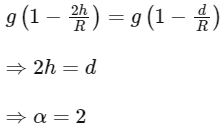


Q25: Two satellites S₁ and S₂ are revolving in circular orbits around a planet with radius R₁ = 3200 km and R₂ = 800 km respectively. The ratio of speed of satellite S₁ to be speed of satellite S₂ in their respective orbits would be 1/x where x = ___________.
Ans: 2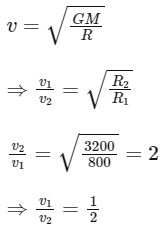

x = 2