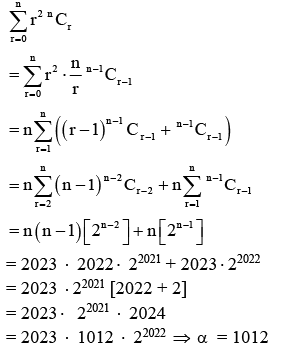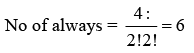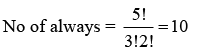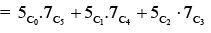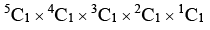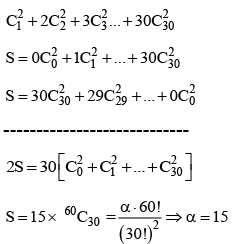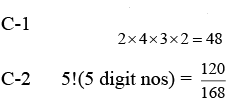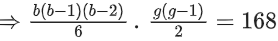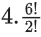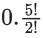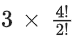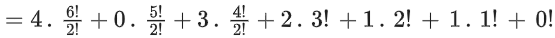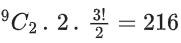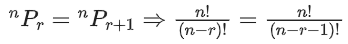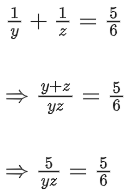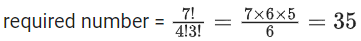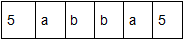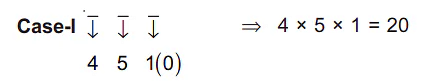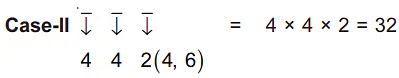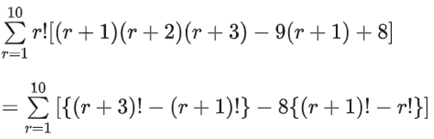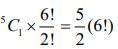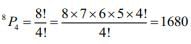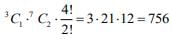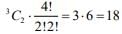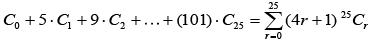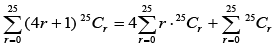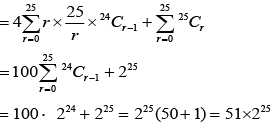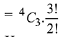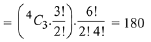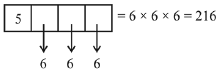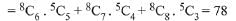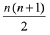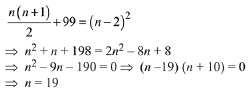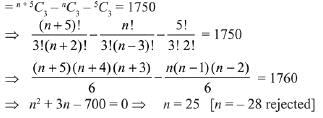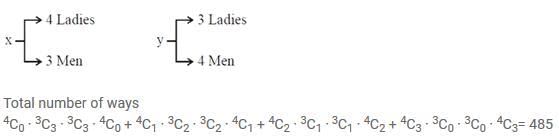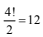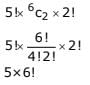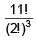JEE Main Previous Year Questions (2016-2025): Permutations and Combinations | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q.1. Suppose 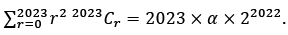 Then the value of α is (JEE Main 2023)
Then the value of α is (JEE Main 2023)
Ans. 1012
Q.2. The number of 9 digit numbers, that can be formed using all the digits of the number 123412341 so that the even digits occupy only even places, is (JEE Main 2023)
Ans. 60
4 even place can be occupied by 4 even digits
Odd place can be occupied by 5 odd digits
Total no. = 6× 10 = 60
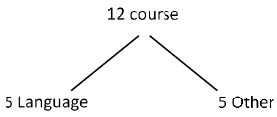
Q.3. A boy needs to select five courses from 12 available courses, out of which 5 courses are language courses. If he can choose at most two language courses, then the number of ways he can choose five courses is (JEE Main 2023)
Ans. 546
(0 language + 5 other) + (1 Language + 4 other) + (2 Language + 3 other)
= 21 + 175 + 350
= 546
Q.4. The number of square matrices of order 5 with entries form the set {0, 1}, such that the sum of all the elements in each row is 1 and the sum of all the elements in each column is also 1, is (JEE Main 2023)
(a) 125
(b) 225
(c) 150
(d) 120
Ans. d
= 120
Q.5. If (30C1)2 + 2 (30C2)2 + 3(30C3)2 + ....+ 30 (30C30)2 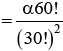 then α is equal to : (JEE Main 2023)
then α is equal to : (JEE Main 2023)
(a) 30
(b) 10
(c) 60
(d) 15
Ans. d
Q.6. The number of integers, greater than 7000 that can be formed, using the digits 3,5,6,7,8 without repetition, is (JEE Main 2023)
(a) 168
(b) 220
(c) 120
(d) 48
Ans. a
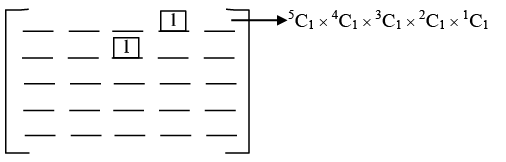
Q.7. Consider 4 boxes, where each box contains 3 red balls and 2 blue balls. Assume that all 20 balls are distinct. In how many different ways can 10 balls be chosen from these 4 boxes so that from each box at least one red ball and one blue ball are chosen? (JEE Advanced 2022)
(a) 21816
(b) 85536
(c) 12096
(d) 156816
Ans. a
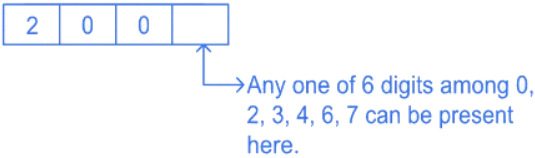
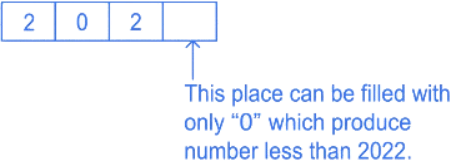
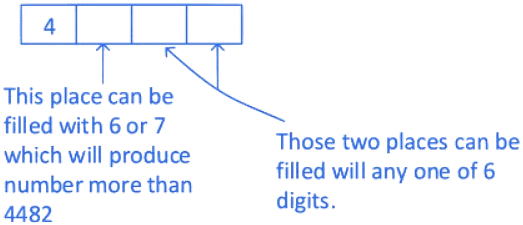
Q.8. The number of 4-digit integers in the closed interval [2022, 4482] formed by using the digits 0, 2, 3, 4, 6, 7 is _________. (JEE Advanced 2022)
Ans. 569
This is a 4-digit integer whose 0th digit called D, 10th digit called C, 100th digit called B and 1000th digit called A.
Given range for possible number is 2022 to 4482.
So, position A can have digits 2, 3 or 4.
0, 6 and 7 can't put in A as number starts with 0, 6 or 7 don't fall in the range between 2022 to 4482.
So, Position A can be filled with 2, 3 or 4 in 3C1 = 3 ways.
Position B can be filled by one of 0, 2, 3, 4, 6, 7
So, total possible ways for position B = 6C1 = 6 ways
Similarly, Position C can be filled in 6C1 = 6 ways
Position D can be filled in 6C1 = 6 ways
∴ Total possible integer numbers starting with 2 or 3 or 4
= 3 × 6 × 6 × 6 = 3 × 216 = 648
Now lets find those numbers which starts with 2 and 4 but don't fall in the range between 2022 to 4482.
Situation 1:∴ Total possible numbers starting with 200 are = 6
Situation 2:
∴ Total possible number in this case = 1
Situation 3:
Total numbers in this case = 2 × 6 × 6 = 72
∴ Total number that don't fall in the range 2022 to 4482 which starts with 2 or 4 are
= 6 + 1 + 72 = 79
∴ Total numbers falls in the range 2022 to 4482
= 648 − 79
= 569
Q.9. Bag I contains 3 red, 4 black and 3 white balls and Bag II contains 2 red, 5 black and 2 white balls. One ball is transferred from Bag I to Bag II and then a ball is drawn from Bag II. The ball so drawn is found to be black in colour. Then the probability, that the transferred ball is red, is: (JEE Main 2022)
(a) 4/9
(b) 5/18
(c) 1/6
(d) 3/10
Ans. b
Q.10. The total number of 5-digit numbers, formed by using the digits 1, 2, 3, 5, 6, 7 without repetition, which are multiple of 6, is (JEE Main 2022)
(a) 36
(b) 48
(c) 60
(d) 72
Ans. d
Q.11. The number of ways to distribute 30 identical candies among four children C1, C2, C3 and C4 so that C2 receives at least 4 and at most 7 candies, C3 receives at least 2 and at most 6 candies, is equal to: (JEE Main 2022)
(a) 205
(b) 615
(c) 510
(d) 430
Ans. d
By multinomial theorem, no. of ways to distribute 30 identical candies among four children C1, C2 and C3, C4
= Coefficient of x30 in (x4 + x5 + .... + x7) (x2 + x3 + .... + x6) (1 + x + x2 ....)2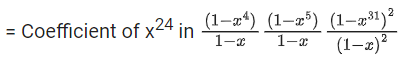
= Coefficient of x24 in (1 − x4 − x5 + x9)(1 − x)−4= 27C24 − 23C20 − 22C19 + 18C15 = 430
Q.12. The number of natural numbers lying between 1012 and 23421 that can be formed using the digits 2, 3, 4, 5, 6 (repetition of digits is not allowed) and divisible by 55 is _________. (JEE Main 2022)
Ans. 6
Q.13. A class contains b boys and g girls. If the number of ways of selecting 3 boys and 2 girls from the class is 168, then b + 3g is equal to _________. (JEE Main 2022)
Ans. 17
bC3 . gC2 = 168
⇒ b (b - 1)(b - 2) g(g - 1) = 25 . 32 . 7
⇒ b (b - 1)(b - 2) g(g - 1) = 6 . 7 . 8 . 3 . 2
∴ b = 8 and g = 3
∴ b + 3g = 17
Q.14. Let S be the set of all passwords which are six to eight characters long, where each character is either an alphabet from {A, B, C, D, E} or a number from {1, 2, 3, 4, 5} with the repetition of characters allowed. If the number of passwords in S whose at least one character is a number from {1, 2, 3, 4, 5} is α × 56, then α is equal to ___________. (JEE Main 2022)
Ans. 7073
If password is 6 character long, then
Total number of ways having atleast one number = 106 − 56
Similarly, if 7 character long = 107 − 57
and if 8-character long = 108 − 58
Number of password = (106 + 107 + 108) − (56 + 57 + 58)
= 56(26 + 5.27 + 25.28 − 1 − 5 − 25)
= 56(64 + 640 + 6400 − 31)
= 7073 × 56
∴ α = 7073
Q.15. Numbers are to be formed between 1000 and 3000, which are divisible by 4, using the digits 1, 2, 3, 4, 5 and 6 without repetition of digits. Then the total number of such numbers is ____________. (JEE Main 2022)
Ans. 30
Q.16. The number of 5-digit natural numbers, such that the product of their digits is 36, is __________. (JEE Main 2022)
Ans. 180
Factors of 36 = 22 . 32 . 1
Five-digit combinations can be (1, 2, 2, 3, 3)
(1, 4, 3, 3, 1), (1, 9, 2, 2, 1)
(1, 4, 9, 11) (1, 2, 3, 6, 1) (1, 6, 6, 1, 1)
i.e., total numbers
= (30 × 3) + 20 + 60 + 10 = 180
Q.17. The letters of the word 'MANKIND' are written in all possible orders and arranged in serial order as in an English dictionary. Then the serial number of the word 'MANKIND' is _____________. (JEE Main 2022)
Ans. 1492
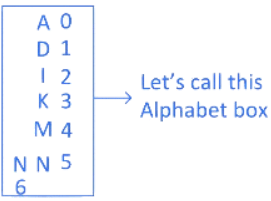
Step 1: Write all the alphabets in alphabetical order.
Step 2: Give a number to each alphabet starting from 0 in alphabetical order.
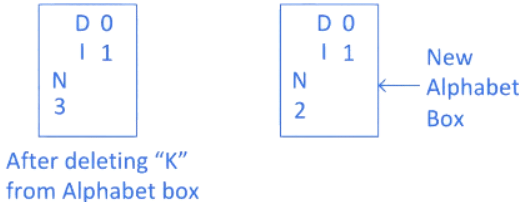
Step 3: In word "MANKIND" first alphabet is "M" which is present in the 4th position in the Alphabet Box. And after "M", in the word "MANKIND" there are 6 alphabets "ANKIND" which can be arrange in 6!/2! ways. Here 2! present because two N presents.
So for alphabet "M" we write
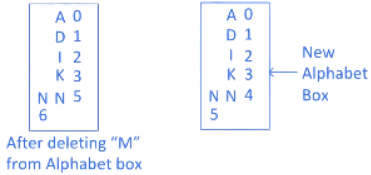
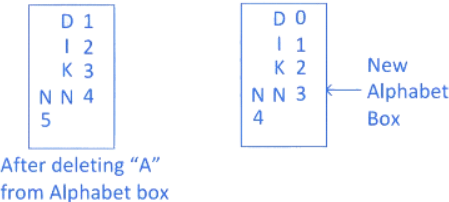
Step 4: As in word "MANKIND" we calculated "M", so delete "M" from alphabet box and check remaining alphabets got right numbers or not in alphabet box.
As you can see after deleting "M", 4th position in the alphabet box is missing so we create a new alphabet box.
Step 5: Now next alphabet after "M" in word "MANKIND" is "A" which is present in the 0th position in the new alphabet box. And after "A" in the word "MANKIND" there are 5 alphabets "NKIND" which can be arrange in 5!/2! ways.
So, for alphabet "A" we write
Step 6: Now in word "MANKIND" we calculated "A", so delete "A" from previous new alphabet box and check remaining alphabets got right numbers or not in alphabet box.
As you can see after deleting "A", 0th positioin in the alphabet box is missing, so we have to create a new alphabet box.
Step 7: Now next alphabet after "A" in word "MANKIND" is "N" which is present in the 3rd and 4th position in the alphabet box. We have to choose minimum position for "N" in the alphabet box. So, we choose 3rd position "N". And after "N" in the word "MANKIND" there are 4 alphabets "KIND" which can be arrange 4!/2! ways. Here 2! used because of 2 N's (one "N" is that "N" which we are considering and other "N" which is present in the word "KIND")
So for alphabet "N" we write
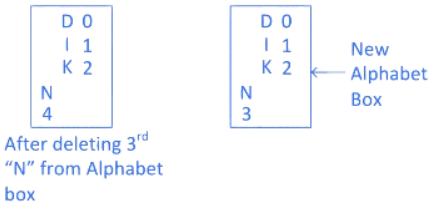
Step 8: Now in word "MANKIND" we calculated "N", so delete 3rd "N" from alphabet box and check remaining alphabets got right number or not in alphabet box. As you can see after deleting 3rd "N", 3rd position is missing in the alphabet box so we have to create a new alphabet box.
Step 9: Now next alphabet after "N" in word "MANKIND" is "K" which is present at the 2nd position in the new alphabet box. And after "K" in the word "MANKIND" there are 3 alphabets "IND" which we can arrange 3! ways.
So for alphabet "K" we write 2 × 3!
Step 10: Now, in word "MANKIND" we calculated "K", so delete "K" from alphabet box and check remaining alphabets got right number or not in alphabet box. As you can see after deleting "K", 2nd position in the alphabet box is missing so we have to create a new alphabet box.
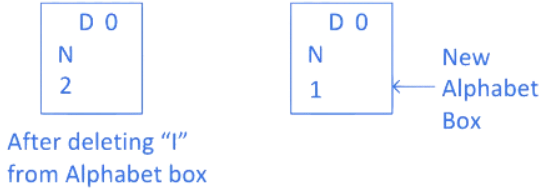
Step 11: Now next alphabet after "K" in word "MANKIND" is "I" which is present at 1st position in the new alphabet box. And after "I" in the word "MANKIND" there are 2 alphabets "ND" which we can arrange in 2! ways. So for alphabet "I" we write 1 × 2!
Step 12: Now in word "MANKIND" we calculated "I", so delete "I" from alphabet box and check remaining alphabets got right numbers or not in alphabet box. As you can see after deleting "I", 1st position in the alphabet box is missing so we have to create a new alphabet box.
Step 13: Now next alphabet after "I" in word "MANKIND" is "N" which is present at 1st position in the new alphabet box. And after "N" in the word "MANKIND" there is 1 alphabet "D" which we can arrange in 1! ways.
So for alphabet "N" we write 1 × 1!.
Step 14: Now in word "MANKIND" we calculated "N", so delete "N" from alphabet box and check remaining alphabets got right numbering or not in alphabet box. As you can see after deleting "N", remaining alphabet "D" got correct numbering so new alphabet box will be same.
Step 15: Now next alphabet after "N" in word "MANKIND" is "D" which is present at the 0th position in the new alphabet box. And after "D" in the word "MANKIND" there is no alphabet so it is the last alphabet.
So for last alphabet we always write 0!
∴ Position of the word "MANKIND" in the dictionary
= 1440 + 0 + 36 + 12 + 2 + 1 + 1
= 1492
Q.18. The number of 6-digit numbers made by using the digits 1, 2, 3, 4, 5, 6, 7, without repetition and which are multiple of 15 is ____________. (JEE Main 2022)
Ans. 360
A number is multiple of 15 when the number is divisible by 5 and sum of digits of the number is divisible by 3.
Among 1, 2, 3, 4, 5, 6, 7 unit place is filled with 5 so it is multiple of 5.
Now to make it divisible by 3, take remaining 5 digits such a way that sum becomes divisible by 3.
Remaining 5 digits can be (1) 1, 2, 3, 4, 6
Here sum = 1 + 2 + 3 + 4 + 6 + 5 = 21 (divisible by 3)
This 5 digits can be filled in those 5 placed without repetition in 5 × 4 × 3 × 2 × 1 = 51 = 120 ways
(2) 2, 3, 4, 6, 7
Here sum = 2 + 3 + 4 + 6 + 7 + 5 = 27 (divisible by 3)
∴ Number of ways = 51 = 120
(3) 1, 2, 3, 6, 7
Here sum = 1 + 2 + 3 + 6 + 7 + 5 = 24 (divisible by 3)
∴ Number of ways = 51 = 120
∴ Total possible 6 digit numbers divisible by 15
= 120 + 120 + 120 = 360
Q.19. In an examination, there are 5 multiple choice questions with 3 choices, out of which exactly one is correct. There are 3 marks for each correct answer, −2 marks for each wrong answer and 0 mark if the question is not attempted. Then, the number of ways a student appearing in the examination gets 5 marks is ____________. (JEE Main 2022)
Ans. 40
Q.20. The total number of four digit numbers such that each of first three digits is divisible by the last digit, is equal to ________. (JEE Main 2022)
Ans. 1086
Q.21. Let b1b2b3b4 be a 4-element permutation with bi ∈ {1, 2, 3, ........, 100} for 1 ≤ i ≤ 4 and bi ≠ bj for i ≠ j, such that either b1, b2, b3 are consecutive integers or b2, b3, b4 are consecutive integers. Then the number of such permutations b1b2b3b4 is equal to ____________. (JEE Main 2022)
Ans. 18915
Q.22. The number of ways, 16 identical cubes, of which 11 are blue and rest are red, can be placed in a row so that between any two red cubes there should be at least 2 blue cubes, is _____________. (JEE Main 2022)
Ans. 56
Q.23. The total number of 3-digit numbers, whose greatest common divisor with 36 is 2, is ___________. (JEE Main 2022)
Ans. 150
∵ x ∈ [100, 999], x ∈ N
Then x/2 ∈ [50, 499], x/2 ∈ N
Number whose G.C.D. with 18 is 1 in this range have the required condition. There are 6 such number from 18 × 3 to 18 × 4. Similarly from 18 × 4 to 18 × 5 ......., 26 × 18 to 27 × 18
∴ Total numbers = 24 × 6 + 6 = 150
The extra numbers are 53, 487, 491, 493, 497 and 499.
Q.24. There are ten boys B1, B2, ......., B10 and five girls G1, G2, ........, G5 in a class. Then the number of ways of forming a group consisting of three boys and three girls, if both B1 and B2 together should not be the members of a group, is ___________. (JEE Main 2022)
Ans. 1120
Number of ways when B1 and B2 are not together
= Total number of ways of selecting 3 boys − B1 and B2 are together
= 10C3 − 8C1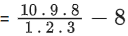
= 112
Number of ways to select 3 girls = 5C3 = 10
∴ Total number of ways = 112 × 10 = 1120
Q.25. The total number of three-digit numbers, with one digit repeated exactly two times, is ______________. (JEE Main 2022)
Ans. 243
C − 1: All digits are non-zero
C − 2: One digit is 0
0, 0, x ⇒ 9C1 . 1 = 9
0, x, x ⇒ 9C1 . 2 = 18
Total = 216 + 27 = 243
Q.26. The number of 3-digit odd numbers, whose sum of digits is a multiple of 7, is _____________. (JEE Main 2022)
Ans. 63
Q.27. The number of 7-digit numbers which are multiples of 11 and are formed using all the digits 1, 2, 3, 4, 5, 7 and 9 is __________. (JEE Main 2022)
Ans. 576
Q.28. Let
S1 = {(i, j, k) : i, j, k ∈ {1, 2, .... ,10}},
S2 = {(i, j) : 1 ≤ i < j + 2 ≤ 10, i, j ∈ {1, 2, ... ,10}},
S3 = {(i, j, k, l) : 1 ≤ i < j < k < l, i, j, k, l ∈ {1, 2, ... ,10}} and
S4 = {(i, j, k, l) : i, j, k and l are distinct elements in {1, 2, ...., 10}.
If the total number of elements in the set Sr is nr, r = 1, 2, 3, 4, then which of the following statements is(are) TRUE? (JEE Advanced 2021)
(a) n1 = 1000
(b) n2 = 44
(c) n3 = 220
(d) n4/12 = 420
Ans. a, b, d
n1 = number of elements in S1 = 10 × 10 × 10 = 1000
n2 = number of elements in S2 = 8 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1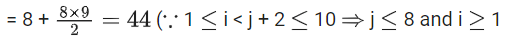
∴ (i = 1, j = 1, 2, 3, .... 8), (i = 2, j = 1, 2, 3, ..... 8), (i = 3, j = 2, 3, 4, .... 8) and so on)
n3 = number of elements in S3 = 10C4
(selecting 4 numbers and arranging in increasing order)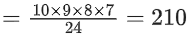
n4 = number of elements in S4 = 10C4 = 10 × 9 × 8 × 7
n4/12 = 420
Q.29. Let P1, P2, ......, P15 be 15 points on a circle. The number of distinct triangles formed by points Pi, Pj, Pk such that i + j + k ≠ 15, is: (JEE Main 2021)
(a) 12
(b) 419
(c) 443
(d) 455
Ans. c
Total number of triangles = 15C3
i + j + k = 15 (Given)
Number of possible triangles using the vertices Pi, Pj, Pk such that i + j + k ≠ 15 is equal to 15C3 − 12 = 443
Q.30. If nPr = nPr+1 and nCr = nCr−1, then the value of r is equal to: (JEE Main 2021)
(a) 1
(b) 4
(c) 2
(d) 3
Ans. c
⇒ (n − r) = 1 .....(1)
nCr = nCr−1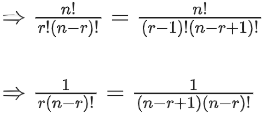
⇒ n − r + 1 = r
⇒ n + 1 = 2r ..... (2)
From (1) and (2), 2r - 1 - r = 1 ⇒ r = 2
Q.31. The sum of all the 4-digit distinct numbers that can be formed with the digits 1, 2, 2 and 3 is: (JEE Main 2021)
(a) 26664
(b) 122664
(c) 122234
(d) 22264
Ans. a
Total possible numbers using 1, 2, 2 and 3 is = 4!/2! = 12
When unit place is 1, the total possible numbers using remaining 2, 2 and 3 are = 3!/2! = 3
When unit place is 2, the total possible numbers using remaining 1, 2 and 3 are = 3! = 6
When unit place is 3, the total possible numbers using remaining 1, 2 and 2 are = 3!/2! = 3
∴ Sum of unit places of all (3 + 6 + 3) 12 numbers is = (1 × 3 + 2 × 6 + 3 × 3)
Similarly,
When 10th place is 1, the total possible numbers using remaining 2, 2 and 3 are = 3!/2! = 3
When 10th place is 2, the total possible numbers using remaining 1, 2 and 3 are = 3! = 6
When 10th place is 3, the total possible numbers using remaining 1, 2 and 2 are = 3!/2! = 3
∴ Sum of 10th places of all (3 + 6 + 3) 12 numbers is = (1 × 3 + 2 × 6 + 3 × 3) × 10
Similarly, Sum of 100th places of all (3 + 6 + 3) 12 numbers is = (1 × 3 + 2 × 6 + 3 × 3) × 100
and Sum of 1000th places of all (3 + 6 + 3) 12 numbers is = (1 × 3 + 2 × 6 + 3 × 3) × 1000
∴ Total sum = (1 × 3 + 2 × 6 + 3 × 3) + (1 × 3 + 2 × 6 + 3 × 3) × 10
+ (1 × 3 + 2 × 6 + 3 × 3) × 100 + (1 × 3 + 2 × 6 + 3 × 3) × 1000
= (3 + 12 + 9) (1 + 10 + 100 + 1000) = 1111 × 24 = 26664
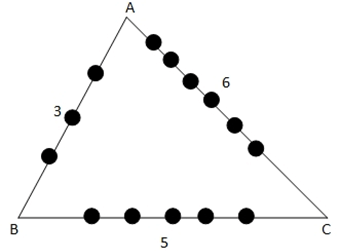
Q.32. If the sides AB, BC and CA of a triangle ABC have 3, 5 and 6 interior points respectively, then the total number of triangles that can be constructed using these points as vertices, is equal to: (JEE Main 2021)
(a) 240
(b) 360
(c) 333
(d) 364
Ans. c
Total number of triangles
= 14C3 − 3C3 − 5C3 − 6C3
= 364 – 31 = 333
Q.33. Team 'A' consists of 7 boys and n girls and Team 'B' has 4 boys and 6 girls. If a total of 52 single matches can be arranged between these two teams when a boy plays against a boy and a girl plays against a girl, then n is equal to: (JEE Main 2021)
(a) 5
(b) 2
(c) 4
(d) 6
Ans. c
Total matches between boys of both team = 7C1 × 4C1 = 28
Total matches between girls of both team = nC16C1 = 6n
Now, 28 + 6n = 52
⇒ n = 4
Q.34. Consider a rectangle ABCD having 5, 7, 6, 9 points in the interior of the line segments AB, CD, BC, DA respectively. Let α be the number of triangles having these points from different sides as vertices and β be the number of quadrilaterals having these points from different sides as vertices. Then (β − α) is equal to: (JEE Main 2021)
(a) 717
(b) 795
(c) 1890
(d) 1173
Ans. a
α = 6C17C19C1 + 5C17C19C1 + 5C16C19C1 + 5C16C17C1
= 378 + 315 + 270 + 210 = 1173
β = 5C16C17C19C1 = 1890
∴ β - α = 1890 - 1173 = 717
Q.35. A natural number has prime factorization given by n = 2x3y5z, where y and z are such that y + z = 5 and y−1 + z−1 = 5/6, y > z. Then the number of odd divisions of n, including 1, is: (JEE Main 2021)
(a) 11
(b) 6
(c) 12
(d) 6x
Ans. c
y + z = 5 ....... (1)
⇒ yz = 6
Also, (y − z)2 = (y + z)2 − 4yz
⇒ (y − z)2 = (y + z)2 − 4yz
⇒ (y − z)2 = 25 − 4(6) = 1
⇒ y − z = 1 ..... (2)
from (1) and (2), y = 3 and z = 2
for calculating odd divisor of p = 2x . 3y . 5z
x must be zero P = 20 . 33 . 52
⇒ Total possible cases = (3050 + 3150 + 3250 + 3350 + .... + 3352)
∴ Total odd divisors must be (3 + 1) ( 2 + 1) = 12
Q.36. The number of seven digit integers with sum of the digits equal to 10 and formed by using the digits 1, 2 and 3 only is: (JEE Main 2021)
(a) 35
(b) 42
(c) 82
(d) 77
Ans. d
(I) First possibility is 1, 1, 1, 1, 1, 2, 3
required number = 7!/5! = 7 × 6 = 42
(II) Second possibility is 1, 1, 1, 1, 2, 2, 2
Total = 42 + 35 = 77
Q.37. The total number of positive integral solutions (x, y, z) such that xyz = 24 is: (JEE Main 2021)
(a) 36
(b) 24
(c) 45
(d) 30
Ans. d
x . y . z = 24
x . y . z = 23 . 31
Three 2 has to be distributed among x, y and z
Each may receive none, one or two
∴ Number of ways = 3+3−1C3−1 = 5C2 ways
Similarly one 3 has to be distributed among x, y and z
∴ Number of ways = 1+3−1C3−1 = 3C2 ways
Total ways = 5C2.3C2 = 30
Q.38. A scientific committee is to be formed from 6 Indians and 8 foreigners, which includes at least 2 Indians and double the number of foreigners as Indians. Then the number of ways, the committee can be formed, is: (JEE Main 2021)
(a) 1050
(b) 575
(c) 560
(d) 1625
Ans. d
Given,
Number of Indians = 6
Number of foreigners = 8
Committee of at least 2 Indians and double number of foreigners is to be formed. Hence, the required cases are
(2I, 4F) + (3I, 6F) + (4I, 8F)
= 6C2 × 8C4 + 6C3 × 8C6 + 6C4 × 8C8
= (15 × 70) + (20 × 28) + (15 × 1)
= 1050 + 560 + 15 = 1625
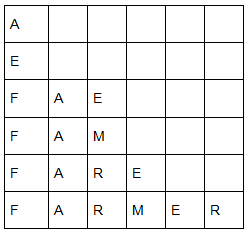
Q.39. All the arrangements, with or without meaning, of the word FARMER are written excluding any word that has two R appearing together. The arrangements are listed serially in the alphabetic order as in the English dictionary. Then the serial number of the word FARMER in this list is ___________. (JEE Main 2021)
Ans. 77
First find all possible words and then subtract words from each case that have both R together.
FARMER (6)
A, E, F, M, R, R
Q.40. The number of six letter words (with or without meaning), formed using all the letters of the word 'VOWELS', so that all the consonants never come together, is ___________. (JEE Main 2021)
Ans. 576
Total possible words = 6! = 720
When 4 consonants are together (V, W, L, S)
such cases = 3! ⋅ 4! = 144 All consonants should not be together
= Total − All consonants together,
= 6! − 3! 4! = 576
Q.41. A number is called a palindrome if it reads the same backward as well as forward. For example 285582 is a six digit palindrome. The number of six digit palindromes, which are divisible by 55, is ____________. (JEE Main 2021)
Ans. 100
For divisible by 55 it shall be divisible by 11 and 5 both, for divisibility by 5 unit digit shall be 0 or 5 but as the number is six digit palindrome unit digit is 5.
A number is divisible by 11 if the difference between sum of the digits in the odd places and the sum of the digits in the even places is a multiple of 11 or zero.
Sum of the digits in the even place = a + b + 5
Sum of the digits in the odd places = a + b + 5
Difference between the two sums = (a + b + 5 ) - (a + b + 5) = 0
0 is divisible by 11.
Hence, 5abba5 is divisible by 11.
So, required number = 10 × 10 = 100
Q.42. The number of three-digit even numbers, formed by the digits 0, 1, 3, 4, 6, 7 if the repetition of digits is not allowed, is ______________. (JEE Main 2021)
Ans. 52
(i) When '0' is at unit placeNumber of numbers = 20
(ii) When 4 or 6 are at unit placeNumber of numbers = 32
Total three digit even number = 20 + 32 = 52
Q.43. Let n be a non-negative integer. Then the number of divisors of the form "4n + 1" of the number (10)10 . (11)11 . (13)13 is equal to ___________. (JEE Main 2021)
Ans. 924
N = 210 × 510 × 1111 × 1313
Now, power of 2 must be zero,
power of 5 can be anything,
power of 13 can be anything
But, power of 11 should be even.
So, required number of divisors is
1 × 11 × 14 × 6 = 924
Q.44. There are 5 students in class 10, 6 students in class 11 and 8 students in class 12. If the number of ways, in which 10 students can be selected from them so as to include at least 2 students from each class and at most 5 students from the total 11 students of class 10 and 11 is 100 k, then k is equal to _____________. (JEE Main 2021)
Ans. 238
Class 10th 11th 12th
Total student 5 6 8
2 3 5 ⇒ 5C2 × 6C3 × 8C5
Number of selection 2 2 6 ⇒ 5C2 × 6C2 × 8C6
3 2 5 ⇒ 5C3 × 6C2 × 8C5
⇒ Total number of ways = 23800
According to question 100 K = 23800
⇒ K = 238
Q.45. If the digits are not allowed to repeat in any number formed by using the digits 0, 2, 4, 6, 8, then the number of all numbers greater than 10,000 is equal to _____________. (JEE Main 2021)
Ans. 96
= 4 × 4 × 3 × 2 = 96
Q.46. There are 15 players in a cricket team, out of which 6 are bowlers, 7 are batsman and 2 are wicketkeepers. The number of ways, a team of 11 players be selected from them so as to include at least 4 bowlers, 5 batsman and 1 wicketkeeper, is ____________. (JEE Main 2021)
Ans. 777
15: Players
6: Bowlers
7: Batsman
2: Wicket keepers
Total number of ways for:
at least 4 bowler, 5 batsman & 1 wicket keeper
= 6C4(7C6 × 2C1 + 7C5 × 2C2) + 6C5 × 7C5 × 2C1
= 777
Q.47. 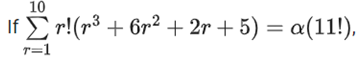 then the value of α is equal to ___________. (JEE Main 2021)
then the value of α is equal to ___________. (JEE Main 2021)
Ans. 4
= (13! + 12! − 2! − 3!) − 8(11! − 1)= (12.13 + 12 − 8).11! − 8 + 8 = (160)(11!)
Therefore, α = 160
Q.48. The missing value in the following figure is (JEE Main 2021)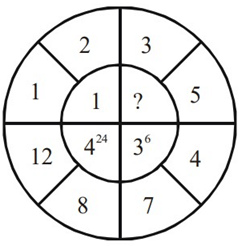
Ans. 4
424 has base 4 (= 12 − 8)
36 has base 3 (= 7 − 4)
(?) will have base 2 ( = 5 − 3)
Power 24 = 6 × 4 = (no. of divisor of 12) × (no. of divisor of 8)
Power 6 = 2 × 3 = (no. of divisor of 7) × (no. of divisor of 4)
(?) will have power = (no. of divisor of 3) × (no. of divisor of 5) = 2 × 2 = 4
Q.49. The number of times the digit 3 will be written when listing the integers from 1 to 1000 is (JEE Main 2021)
Ans. 300
In single digit numbers = 1
In double digit numbers = 10 + 9 = 19
In triple digit numbers = 100 + 90 + 90 = 280
Total = 300 times
Q.50. The total number of numbers, lying between 100 and 1000 that can be formed with the digits 1, 2, 3, 4, 5, if the repetition of digits is not allowed and numbers are divisible by either 3 or 5, is ________. (JEE Main 2021)
Ans. 32
The numbers are lying between 100 and 1000 then each number is of three digits.
The possible combination of 3 digits numbers are
1, 2, 3; 1, 2, 4; 1, 2, 5; 1, 3, 4; 1, 3, 5; 1, 4, 5; 2, 3, 4; 2, 3, 5; 2, 4, 5; and 3, 4, 5.
The possible combination of numbers which are divisible by 3 are 1, 2, 3; 3, 4, 5; 1, 3, 5 and 2, 3, 4.
(If sum of digits of a number is divisible by 3 then the number is divisible by 3)
∴ Total number of numbers = 4 × 3! = 24
The possible combination of numbers divisible by 5 are 1, 2, 5; 2, 3, 5; 3, 4, 5; 1, 3, 5; 1, 4, 5 and 2, 4, 5.
(If the last digit of a number is 0 or 5 then the number is divisible by 5)
∴ Total number of numbers = 6 × 2! = 12
The possible combination of number divisible by both 3 and 5 are 1, 3, 5 and 3, 4, 5.
∴ Total number of numbers = 2 × 2! = 4
∴ Total required number = 24 + 12 - 4 = 32
Q.51. The sum of first four terms of a geometric progression (G. P.) is 65/12 and the sum of their respective reciprocals is 65/18. If the product of first three terms of the G.P. is 1, and the third term is α, then 2α is _________. (JEE Main 2021)
Ans. 3
Let the terms are a, ar, ar2, ar3
a + ar + ar2 + ar3 = 65/12 ..........(1)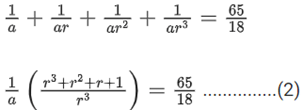
Doing (1)/(2),
a2r3 = 18/12 = 3/2
Also given, a3r3 = 1 ⇒ a(3/2) = 1 ⇒ a = 2/3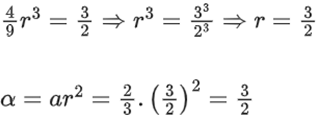
2α = 3
Q.52. The students S1, S2, ....., S10 are to be divided into 3 groups A, B and C such that each group has at least one student and the group C has at most 3 students. Then the total number of possibilities of forming such groups is ___________. (JEE Main 2021)
Ans. 31650
If group C has one student then number of groups
= 10C1 [29 – 2] = 5100
If group C has two students then number of groups
= 10C2 [28 – 2] = 11430
If group C has three students then number of groups
= 10C3 × [27 – 2] = 15120
So total groups = 31650
Q.53.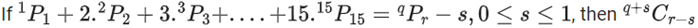 is equal to ______________. (JEE Main 2021)
is equal to ______________. (JEE Main 2021)
Ans. 136
1P1 + 2.2P2 + 3.3P3 + .... + 15.15P15
= 1! + 2 . 2! + 3 . 3! + ..... 15 × 15!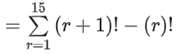
= 16! − 1
= 16P16 − 1
⇒ q = r = 16, s = 1
q+sCr−s = 17C15 = 136
Q.54. Total number of 6-digit numbers in which only and all of the five digits 1, 3, 5, 7 and 9 appear, is (2020)
(a) 1/2 (6!)
(b) 6!
(c) 56
(d) 5/2 (6!)
Ans. d
For digit to repeat, we have 5C1 choices and six digits can be arranged in 6!/2! ways. Hence, total number of 6-digit numbers in which only and all the five digits 1, 3, 5, 7 and 9 appear, is
Q.55. The number of ordered pairs (r, k) for which 6.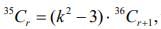 where k is an integer, is (2020)
where k is an integer, is (2020)
(a) 3
(b) 2
(c) 6
(d) 4
Ans. d
We have................ (1)
and (k2 − 3) > 0
k2 > 3 .............. (2)
Now, the possible values of r for integral values of k are 5 and 35. Hence, the number of order pairs are (5, 2), (5, -2), (35, 3) and (35, -3).
Q.56. An urn contains 5 red marbles, 4 black marbles and 3 white marbles. Then the number of ways in which 4 marbles can be drawn so that at most three of them are red is ______. (2020)
Ans. 490.00
Total marbles are 5 red, 4 black and 3 white.
4 marbles are drawn, atmost 3 of them are red.
Case are:
3R and 1 other → 5C3 × 7C1 =70
2R and 2 other → 5C2 × 7C2 =210
1R and 3 other → 5C1 × 7C3 = 175
Zero R and 4 other → 5C0 × 7C4 = 35
Total = 490
Q.57. If a, b and c are the greatest values of 19Cp, 20Cq and 21Cr respectively, then (2020)
(a) a/11 = b/22 = c/21
(b) a/10 = b/11 = c/21
(c) a/11 = b/22 = c/42
(d) a/10 = b/11 = c/42
Ans. c
We know that the value of nCr is maximum at its middle term. So,
a = 19Cp = 19C10 = 19C9 ..............(i)
b = 20Cp = 20C10 = 2.20C9 ..............(ii)
c = 21Cr = 21C11 = 21/11.20C10 ..............(iii)
Now, b = 2a and c = 21/11 b = 42/11a
a : b : c = 11: 22 : 42
Hence, a/11 = b/22 =c/42
Q.58. The number of 4 letter words (with or without meaning) that can be formed from the eleven letters of the word ‘EXAMINATION’ is _______. (2020)
Ans. 2454.00
The word EXAMINATION has 2N, 2A, 2I, E, X, M, T and O.
Case 1: All are different, so
Case 2: Two same and two are different, so
Case 3: Two same and other two same, so
Hence, total number of 4 letter words = 1680 + 756 + 18 = 2454
Q.59. If the number of five digit numbers with distinct digits and 2 at the 10th place is 336 k, then k is equal to (2020)
(a) 4
(b) 6
(c) 7
(d) 8
Ans. d
We have
Number of such numbers = 8 x 8 x 7 x 6 = 336k=> k = 2688/336 = 8
Q.60. If Cr = 25Cr and C0 + 5.C1 + 9.C2 +...........+ (101) . C25 = 225.k, then k is equal to ________. (2020)
Ans. 51.00
We have
Q.61. Consider a class of 5 girls and 7 boys. The number of different teams consisting of 2 girls and 3 boys that can be formed from this class, if there are two specific boys A and B, who refuse to be the members of the same team, is: (2019)
(a) 500
(b) 200
(c) 300
(d) 350
Ans. c
Since, the number of ways to select 2 girls is 5C2.
Now, 3 boys can be selected in 3 ways.
(a) Selection of A and selection of any 2 other boys (except B) in 5C2 ways
(b) Selection of B and selection of any 2 two other boys (except A) in 5C2 ways
(c) Selection of 3 boys (except A and B) in 5C3 ways Hence, required number of different teams
= 5C2 (5C2 + 5C2 + 5C3) = 300
Q.62. The number of natural numbers less than 7,000 which can be formed by using the digits 0, 1, 3, 7, 9 (repetition of digits allowed) is equal to: (2019)
(a) 374
(b) 372
(c) 375
(d) 250
Ans. a
Number of numbers with one digit = 4 = 4
Number of numbers with two digits = 4 x 5 = 20
Number of numbers with three digits = 4 x 5 x 5 = 100
Number of numbers with four digits = 2 x 5 x 5 x 5 = 250
∴ Total number of numbers = 4 + 20 + 100 + 250 = 374
Q.63. In a class of 140 students numbered from 1 to 140, all even numbered students opted Mathematics course, those whose number is divisible by 3 opted Physics course and those whose number is divisible by 5 opted Chemistry course. Then the number of students who did not opt for any of the three courses is: (2019)
(a) 102
(b) 42
(c) 1
(d) 38
Ans. d
⇒ Number of required students
= 140 - (4 + 19 + 5 + 10 + 37 + 18 + 9)
= 140 - 102 = 38
Q.64. The sum of all two digit positive numbers which when divided by 7 yield 2 or 5 as remainder is: (2019)
(a) 1256
(b) 1465
(c) 1365
(d) 1356
Ans. d
Two digit positive numbers which when divided by 7 yield 2 as remainder are 12 terms i.e,16, 23, 30, ..., 93
Two digit positive numbers which when divided by 7 yield 5 as remainder are 13 terms i.e, 12, 19, 26, ..., 96
By using AP sum of 16, 23, ..., 93, we get
S1 = 16 + 23 + 30 + ... + 93 = 654
By using AP sum of 12, 19, 26, ..., 96, we get
S2= 12 + 19 + 26 + ... + 96 = 702
Required Sum = S1 + S2 = 654 + 702
= 1356
Q.65. The number of functions f from {1, 2, 3, ...., 20} onto {1, 2, 3, ...., 20} such that f(k) is a multiple of 3, whenever k is a multiple of 4 is: (2019)
(a) 65 x (15)!
(b) 5! x 6!
(c) (15)! x 6!
(d) 56 x 15
Ans. c
Domain and codomain = {1, 2, 3, ..., 20}.
There are five multiple of 4 as 4, 8, 12, 16 and 20. and there are 6 multiple of 3 as 3, 6, 9, 12, 15, 18.
Since, whenever k is multiple of 4 then f(k) is multiple of 3 then total number of arrangement
= 6c5 x 5! = 6!
Remaining 15 elements can be arranged in 15! ways. Since, for every input, there is an output
⇒ function f(k) in onto
∴ Total number of arrangement =15! х 6!
Q.66. Consider three boxes, each containing 10 balls labelled 1,2, ..., 10. Suppose one ball is randomly drawn from each of the boxes. Denote by ni, the label of the ball drawn from the ith box, (i = 1, 2, 3). Then, the number of ways in which the balls can be chosen such that n1 < n2 < n3 is: (2019)
(a) 120
(b) 82
(c) 240
(d) 164
Ans. a
Collecting different labels of balls drawn =10 x 9 x 8
∵ Arrangement is not required.
∴ The number of ways in which the balls can be chosen is,
Q.66. Let S= {1,2,3, ..., 100}. The number of non-empty subsets A of S such that the product of elements in A is even is: (2019)
(a) 2100 -1
(b) 250(250-1)
(c) 250 - 1
(d) 250+1
Ans. b
∵ Product of two even number is always even and product of two odd numbers is always odd.
∴ Number of required = Total number of subsets
subsets - Total number of subsets having only odd numbers
= 2100 - 250
= 250(250 - 1)
Q.68. All possible numbers are formed using the digits 1, 1, 2, 2, 2, 2, 3, 4, 4 taken all at a time. The number of such numbers in which the odd digits occupy even places is: (2019)
(a) 180
(b) 175
(c) 160
(d) 162
Ans. a
∵ There are total 9 digits and out of which only 3 digits are odd.
∴ Number of ways to arrange odd digits first
Hence, total number of 9 digit numbers
Q.69. The sum of all natural numbers such that 100 < n < 200 and H.C.F. (91, n) > 1 is: (2019)
(a) 3203
(b) 3303
(c) 3221
(d) 3121
Ans. d
∵ 91 =13 x 7
Then, the required numbers are either divisible by 7 or 13.
∴ Sum of such numbers = Sum of no. divisible by 7 + sum of the no. divisible by 13 - Sum of the numbers divisible by 91.
= (105 + 112 + ... + 196)+ (104+ 117+ ...+195) - 182
= 2107 + 1196 - 182
= 3121
Q.70. The number of four-digit numbers strictly greater than 4321 that can be formed using the digits 0, 1, 2, 3, 4, 5 (repetition of digits is allowed) is: (2019)
(a) 288
(b) 360
(c) 306
(d) 310
Ans. d
0, 1, 2, 3, 4, 5
Number of four-digit number starting with 5 is,
Number of four-digit numbers starting with 45 is,
Number of four-digit numbers starting with 44 is,
Number of four-digit numbers starting with 43 and greater than 4321 is,
Number of four-digit numbers starting with 432 and greater than 4321 is.
Hence, required numbers = 216 + 36 + 36 + 18 + 4 = 310.
Q.71. A committee of 11 members is to be formed from 8 males and 5 females. If m is the number of ways the committee is formed with at least 6 males and n is the number of ways the committee is formed with at least 3 females, then: (2019)
(a) m + n = 68
(b) m = n = 78
(c) n = m - 8
(d) m = n = 68
Ans. b
Since, m = number of ways the committee is formed with at least 6 males
and n = number of ways the committee is formed with at least 3 females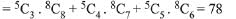
Hence m = n = 78.
Q.72. Some identical balls are arranged in rows to form an equilateral triangle. The first row consists of one ball, the second row consists of two balls and so on. If 99 more identical balls are added to the total number of balls used in forming the equilateral triangle, then all these balls can be arranged in a square whose each side contains exactly 2 balls less than the number of balls each side of the triangle contains. Then the number of balls used to form the equilateral triangle is: (2019)
(a) 157
(b) 262
(c) 225
(d) 190
Ans. d
Number of balls used in equilateral triangle =
∵ side of equilateral triangle has n-balls
∴ no. of balls in each side of square is = (n - 2)
According to the question,
Number of balls used to form triangle
Q.73. The number of 6 digit numbers that can be formed using the digits 0, 1, 2, 5, 7 and 9 which are divisible by 11 and no digit is repeated, is: (2019)
(a) 72
(b) 60
(c) 48
(d) 36
Ans. b
Given digit 0, 1,2, 5, 7, 9
Number of ways to arranging them
= 3! x 3! + 3! x 2 x 2 = 6 x 6 + 6 x 4 = 6 x 10 = 60
Q.74. Suppose that 20 pillars of the same height have been erected along the boundary of a circular stadium. If the top of each pillar has been connected by beams with the top of all its non-adjacent pillars, then the total number of beams is: (2019)
(a) 170
(b) 180
(c) 210
(d) 190
Ans. a
Total number of beams = 20C2 - 20 = 190 - 20= 170
Q.75. The number of ways of choosing 10 objects out of 31 objects of which 10 are identical and the remaining 21 are distinct is: (2019)
(a) 220 - 1
(b) 221
(c) 220
(d) 220+1
Ans. c
Number of ways of selecting 10 objects
= (10I, 0D) or (9I, ID) or (8I, ID) or ... (0I, 10D)
Here, D signifies distinct object and 7 indicates identical object
Q.76. A group of students comprises of 5 boys and n girts. If the number of ways, in which a team of 3 students can randomly be selected from this group such that there is at least one boy and at least one girl in each team, is 1750, then n is equal to: (2019)
(a) 28
(b) 27
(c) 25
(d) 24
Ans. c
Number of ways of selecting three persons such that there is atleast one boy and atleast one girl in the selected persons
Q.77. From 6 different novels and 3 different dictionaries, 4 novels and 1 dictionary are to be selected and arranged in a row on a shelf so that the dictionary is always in the middle. The number of such arrangements is: (2018)
(a) At least 1000
(b) Less than 500
(c) At least 500 but less than 750
(d) At least 750 but less than 1000
Ans. a
Dictionary can be chosen in 3C1 = 3 ways
Novels can be arranged in 6C4 4! = 360 ways.
N = 3 x 360 = 1080
Q.78. n-digit numbers are formed using only three digits 2, 5 and 7. The smallest value of n for which 900 such distinct numbers can be formed, is: (2018)
(a) 7
(b) 8
(c) 9
(d) 6
Ans. a
For each place we have 3 choices
(i) for n - digits 3 × 3 … n times = 3n > 900
n = 7
Q.79. The number of numbers between 2,000 and 5,000 that can be formed with the digits 0, 1, 2, 3, 4 (repetition of digits is not allowed) and are multiple of 3 is: (2018)
(a) 36
(b) 30
(c) 24
(d) 48
Ans. b
There are 4 places to be filled with the given digits. The thousands place can have only 2, 3 and 4 since the number has to be greater than 2000. For the remaining 3 places, we have pick out digits such that the resultant number is divisible by 3. The divisibility criteria for 3 states that sum of digits of the number should be divisible by 3.
Case 1: if we pick 2 for thousand place. The remaining digits we can pick such that sum of digits at all places is a multiple of 3 are: 0,1 and 3 as 2 + 1 + 0 + 3 = 6 is divisible by 3. 0,3 and 4 as 2 + 3 + 0 + 4 = 9 is divisible by 3. In both the above combination, the remaining three digits can be arranged in 3! ways. Total number = 2 × 3! = 12
Case 2: If we pick 3 for thousands place. The remaining digits we can pick such that sum of digits at all places is a multiple of 3 are: 0, 1 and 2 as 3 + 1 + 0 + 2 = 6 is divisible by 3. 0,2 and 4 as 3 + 2 + 0 + 4 = 9 is divisible by 3. In both the above combinations, the remaining three digits can be arranged in 3! ways. Total number=2 × 3! = 12
Case 3: if we pick 4 for thousand place. The remaining digits we can pick such that sum of digits at all places is a multiple of 3 are: 0,2 and 3 as 4 + 2 + 0 + 3 = 9 is divisible by 3. In the above combination, the remaining three digits can be arranged in 3! ways. Total number = 3! = 6.
Total number of numbers between 2000 and 5000 divisible by 3 are 12 + 12 + 6 = 30
Q.80. A man X has 7 friends, 4 of them are ladies and 3 are men. His wife Y also has 7 friends, 3 of them are ladies and 4 are men. Assume X and Y have no common friends. Then the total number of ways in which X and Y together can throw a party inviting 3 ladies and 3 men, so that 3 friends of each of X and Y are in this party, is (2017)
(a) 484
(b) 485
(c) 468
(d) 469
Ans. b
Q.81. If all the words, with or without meaning, are written using the letters of the word QUEEN and are arranged as in English dictionary, then the position of the word QUEEN is: (2017)
(a) 47th
(b) 45th
(c) 46th
(d) 44th
Ans. c
E, E, N, Q, U
(i) E......... = 24
(ii) N ......... =
(iii) Q E........ = 3! = 6
(iv) Q N ......=
(v) Q U E E N = 1
Total = (i) + (ii) + (iii) + (iv) + (v) = 46th
Q.82. The number of ways in which 5 boys and 3 girls can be seated on a round table if a particular boy B1 and a particular girl G1 never sit adjacent to each other, is: (2017)
(a) 7!
(b) 5 × 6!
(c) 6 × 6!
(d) 5 × 7!
Ans. b
4 boy and 2 girls in circle
Q.83. If all the words (with or without meaning) having five letters, formed using the letters of the word SMALL and arranged as in a dictionary; then the position of the word SMALL is: (2016)
(a) 46th
(b) 59th
(c) 52nd
(d) 58th
Ans. d
A LL MS
Total words = 12 + 24 + 12 + 3 + 6 = 57 .
SMALL 58th
∴ The position of the word SMALL is 58th
Q.84. If the four letter words (need not be meaningful) are to be formed using the letters from the word “MEDITERRANEAN” such that the first letter is R and the fourth letter is E, then the total number of all such words is: (2016)
(a) 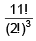
(b) 59
(c) 110
(d) 56
Ans. a
There are 1M, 3E, 1D, II, IT, 2R, 2A, 2N
R– –E – – –– –– –– –– ––
Rest of the 11 letters can be arranged in
|
347 docs|185 tests
|