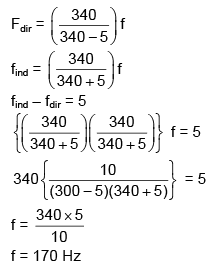Q.1. A stationary observer receives sound from two identical tuning forks, one of which approaches and the other one recedes with the same speed (much less than the speed of sound). The observer hears 2 beats/s. The oscillation frequency of each tuning fork is f0 = 1400 Hz and the velocity of sound in air is 350m/s. The speed of each tuning fork is close to (2020)
(1) 1/2 m/s
(2) 1 m/s
(3) 1/4 m/s
(4) 1/8 m/s
Ans. (3)
Solution.
Given that, beats, n = 2
f0 = 1400 Hz
v = 350 m/s
Observer receives sound from two force, one approaching and one receding.
So apparent frequency from the two forks will be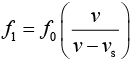
and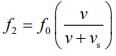
vs is speed of source.
We know that, beat is given by n = f1 – f2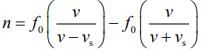
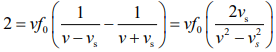
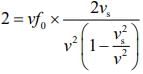
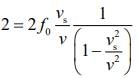
Since, vs << v
1 = fo x vs/v
vs = v/fo = 350/1400 = 1/4
So, the speed of each tuning fork is 1/4 m/s
Q.2. A 1m long (both ends open) organ pipe is kept in a gas that has double the density of air at STP. Assuming the speed of sound in air at STP is 300 m/s, the frequency difference between the fundamental and second harmonic of this pipe is _________ Hz. (2020)
Ans. (106)
Solution.
Given that L = 1m, ρgas = 2ρair, νair = 300m/s
Velocity of a sound in the medium is given by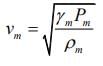
Since, 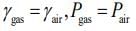
So, 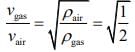
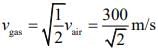
Frequency difference between fundamental and second harmonic of open organ pipe is given by
= 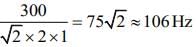
Q.3. A transverse wave travels on a taut steel wire with a velocity of v when tension in it is 2.06 × 104 N. When the tension is changed to T, the velocity changed to v/2. The value of T is close to (2020)
(1) 2.50 × 104 N
(2) 5.15 × 103 N
(3) 30.5 × 104 N
(4) 10.2 × 102 N
Ans. (2)
Solution.
Given that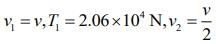
Velocity in the string is given by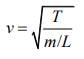
Since, m and L are constant v ∝ T
So, 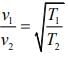
Therefore,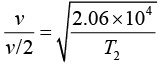
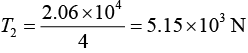
Q.4. Three harmonic waves having equal frequency v and same intensity I0, have phase angles, 0, π/4 and −π /4 respectively. When they are superimposed, the intensity of the resultant wave is close to (2020)
(1) 5.8I0
(2) 0.2I0
(3) 3I0
(4) I0
Ans. (1)
Solution.
General equation of wave is
x = A sin(2πvt± ϕ)
Where A is the amplitude of wave, n is frequency of the wave and f is the phase angle of the wave.
We have three waves with phase angles 0, π/4, -π/4. So,
x1 = Asin(2πvt)
x2 = Asin(2πvt + π/4)
x3 = Asin(2πvt - π/4)
Resultant wave when we superimposed these three waves are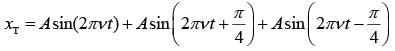
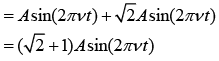
The amplitude of the resultant wave is (√2 + 1)A.
We know that I ∝ A2
So,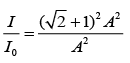
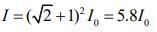
Q.5. A wire of length L and mass per unit length 6.0 x 10-3 kg/m is put under tension of 540 N. Two consecutive frequencies that it resonates at are 420 Hz and 490 Hz. Then L in meters is (2020)
(1) 2.1 m
(2) 1.1 m
(3) 8.1 m
(4) 5.1 m
Ans. (1)
Solution.
Given that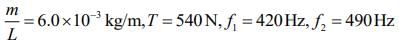
Resonant frequency is given by
So,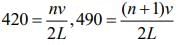
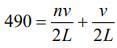
490 = 420 + ν/2L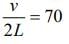
Velocity of wave in a wire is given by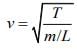
So,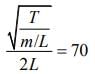
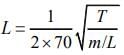
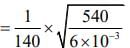
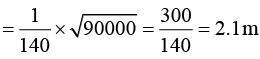
Q 6. A musician using an open flute of length 50 cm produces second harmonic sound waves. A person runs toward the musician from another end of a hall at a speed of 10 km/h. If the wave speed is 330 m/s, the frequency heard by the running person shall be close to (2019)
(1) 666 Hz
(2) 753 Hz
(3) 500 Hz
(4) 333 Hz
Ans: (1)
Solution:
f is frequency of sound produced by a flute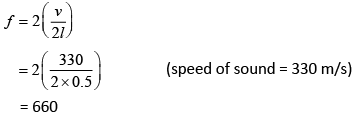
Velocity of observer, vo = 10 km/h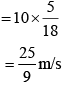
Frequency observed by observer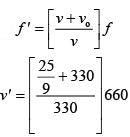
= 335.56 × 2 = 671.12 ≈ 666 Hz
Q 7. A train moves toward a stationary observer with speed 34 m/s. The train sounds a whistle and its frequency registered by the observer is f1. If the speed of the train is reduced to 17 m/s, the frequency registered is f2. If speed of sound is 340 m/s, then the ratio f1/f2 is (2019)
(1) 8/17
(2) 19/18
(3) 20/19
(4) 21/20
Ans:(2)
Solution:
As we know that,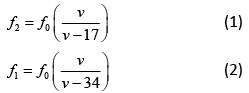
Dividing Eq. (2) by Eq. (1), we get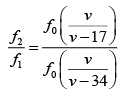
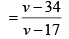 [speed of sound v = 340 m/s]
[speed of sound v = 340 m/s]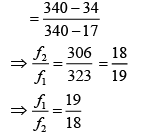
Q 8. A closed organ pipe has a fundamental frequency of 1.5 kHz. The number of overtones that can be distinctly heard by a person with this organ pipe will be (assume that the highest frequency a person can hear is 20,000 Hz) (2019)
(1) 6
(2) 4
(3) 7
(4) 5
Ans: (1)
Solution:
For closed organ pipe, resonate frequency is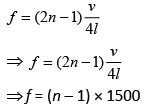
fmax for audible frequency = 20,000 Hz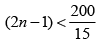
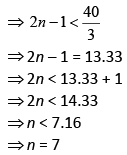
Therefore, number of overtones = n – 1 = 7 – 1= 6
Q 9. The equation of a traveling wave on a stretched string of linear density 5 g/m is y = 0.03 sin(450t − 9x) where distance and time are measured in SI units. The tension in die string is (2019)
(1) 5 N
(2) 75 N
(3) 10 N
(4) 12.5 N
Ans: (4)
Solution:
We have,
y = 0.03 sin (450 t – 9x)
General wave equation is,
y = a sin (ωt – kx)
So,
ω = 450
k = 9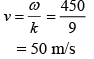
We also know that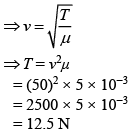
Q 10. A person standing on an open ground hears the sound of a jet aeroplane coming from north at an angle 60° with ground level. But he finds the aeroplane right vertically above his position. If v is the speed of sound, speed of the plane is (2019)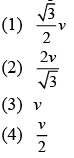
Ans: (4)
Solution: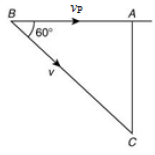
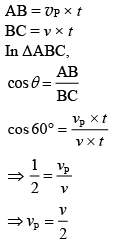
Q 11. A heavy ball of mass M is suspended from the ceiling of a car by a light string of mass m(m << M). When the car is at rest, the speed of transverse waves in the string is 60 m/s. When the car has acceleration a, the wave-speed increases to 60.5 m/s. The value of a, in terms of gravitational acceleration g, is closest to (2019)
(1) g/30
(2) g/5
(3) g/10
(4) g/20
Ans: (2)
Solution: We know that when car is at rest velocity of wave is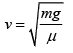 (1)
(1)
When the car has accelerated velocity is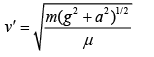 (2)
(2)
Dividing Eq. (2) by Eq. (1), we have
Using binomial expansion, we have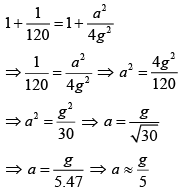
Q 12. A string of length 1 m and mass 5 g is fixed at both ends. The tension in the string is 8.0 N. The string is set into vibration using an external vibrator of frequency 100 Hz. The separation between successive nodes on the string is close to (2019)
(1) 10.0 cm
(2) 33.3 cm
(3) 16.6 cm
(4) 20.0 cm
Ans: (4)
Solution: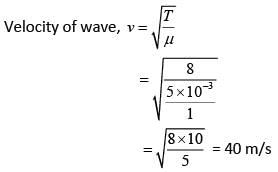
Wavelength of wave v = fλ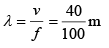
Therefore, distance between two consecutive nodes = λ/2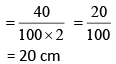
Q 13. A resonance tube is old and has jagged end. It is still used in the laboratory to determine velocity of sound in air. A tuning fork of frequency 512 Hz produces first resonance when the tube is filled with water to a mark 11 cm below a reference mark, near the open end of the tube. The experiment is repeated with another fork of frequency 256 Hz which produces first resonance when water reaches a mark 27 cm below the reference mark. The velocity of sound in air, obtained in the experiment, is close to (2018)
(1) 322 m/s
(2) 341 m/s
(3) 335 m/s
(4) 328 m/s
Ans: (4)
Solution:
Let f be the frequency
For f = 512 Hz, marked 11 cm below reference mark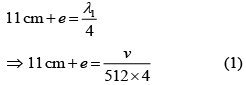
For f = 256 Hz marked 27 cm below reference mark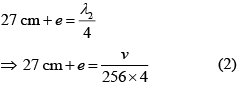
From Eq. (1) and Eq. (2), we get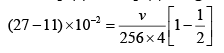
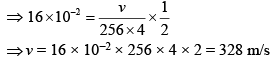
Q 14. A granite rod of 60 cm length is clamped at its middle point and is set into longitudinal vibrations. The density of granite is 2.7 x 103 kg/m3 and its Young's modulus is 9.27 x 1010 Pa. What will be the fundamental frequency of the longitudinal vibrations ? (2018)
(1) 5 kHz
(2) 2.5 kHz
(3) 10 kHz
(4) 7.5 kHz
Ans: (1)
Solution:
Since rod is clamped at centre. So centre it behaves as node & end it behave as antinode.
So,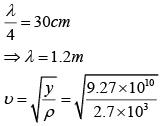
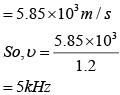
Q 15. A tuning fork vibrates with frequency 256 Hz and gives one beat per second with the third normal mode of vibration of an open pipe. What is the length of the pipe? (Speed of sound in air is 340 ms-1) (2018)
(1) 180 cm
(2) 190 cm
(3) 220 cm
(4) 200 cm
Ans: (4)
Solution:
Third normal mode of frequency in open pipe,
f = 3Vs/2l
Where, Vs = 340m/s
Get L = 2m
Or
L = 200 cm
Q 16. The end correction of a resonance column is 1cm. If the shortest length resonating with the tuning fork is 10cm, the next resonating length should be: (2018)
(1) 32cm
(2) 40cm
(3) 28cm
(4) 36cm
Answer: (1)
Solution:
Given : e = 1 cm
For first resonance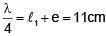
For second resonance
⇒ ℓ2 = (3 × 11) - 1 = 32 cm
Q 17. Two sitar strings A and B playing the note 'Dha' are slightly out of tune and produce beats of frequency 5Hz. The tension of the string B is slightly increased and the beat frequency is found to decrease by 3Hz. If the frequency of A is 425 Hz. The original frequency of B is: (2018)
(1) 428 Hz
(2) 430 Hz
(3) 422 Hz
(4) 420 Hz
Ans: D
Solution:
Frequency of B is either 420Hz or 430Hz. As tension in B is increased its frequency will increase. If frequency is 430Hz, beat frequency will increase. If frequency is 420 Hz beat frequency will decrease, hence correct answer is 420Hz
Q 18. An observer is moving with half the speed of light towards a stationary microwave source emitting waves at frequency 10 GHz. What is the frequency of the microwave measured by the observer? (speed of light = 3 × 108 ms-1) (2017)
(1) 17.3 GHz
(2) 15.3 GHz
(3) 10.1 GHz
(4) 12.1 GHz
Ans: (1)
Solution:
For relativistic motion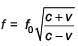 ;
;
v = relative speed of approach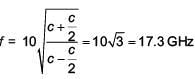
Q 19. Two wires W1 and W2 have the same radius r and respective densities r1 and r2 such that ρ2 = 4ρ1.
They are joined together at the point O, as shown in the figure. The combination is used as a sonometer wire and kept under tension T. The point O is midway between the two bridges. When a stationary wave is set up in the composite wire, the joint is found to be a node. The ratio of the number of antinodes formed in W1 to W2 is - (2017)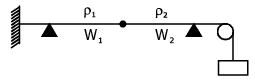
(1) 4 : 1
(2) 1 : 2
(3) 1 : 1
(4) 1 : 3
Ans: (2)
Solution: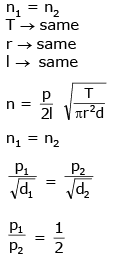
Q 20. A standing wave is formed by the superposition of two waves travelling in opposite directions. The transverse displacement is given by 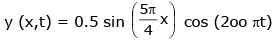
What is the speed of the travelling wave moving in the positive x direction ? (x and t are in meter and second, respectively.) (2017)
(1) 120 m/s
(2) 90 m/s
(3) 160 m/s
(4) 180 m/s
Ans: (3)
Solution: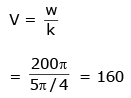
Q 21. A uniform string of length 20 m is suspended from a rigid support. A short wave pulse in introduced at its lowest end. It starts moving up the string. The time taken to reach the support is: (2016)
(take g = 10 ms-2)
(1) 2π√2s
(2) 2s
(3) 2√2s
(4) √2s
Ans: (3)
Solution: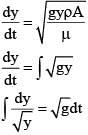
Q 22. A pipe open at both ends has a fundamental frequency 'f' in air. The pipe is dipped vertically in water so that half of it is in water. The fundamental frequency of the air column now is: (2016)
(1) f/2
(2) 3f/4
(3) 2f
(4) f
Ans: D
Solution:
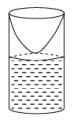
Q 23. Two engines pass each other moving in opposite directions with uniform speed of 30m/s. One of them is blowing a whistle of frequency 540 Hz. Calculate the frequency heard by driver of second engine before pass each other. Speed sound is 330 m/sec. (2016)
(1) 540 Hz
(2) 648 Hz
(3) 270 Hz
(4) 450 Hz
Ans: (2)
Solution:
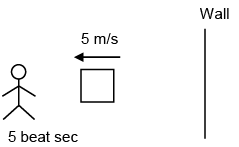
Q 24. A toy- car ,blowing its horn, is moving with a steady speed of 5 m/s, away from a wall. An observer, towards whom the toy car is moving, is able to hear 5 beat per second. If the velocity of sound in air is 340 m/s, the frequency of horn of the toy car is close to : (2016)
(1) 340Hz
(2) 170 Hz
(3) 510 Hz
(4) 680 Hz
Ans: (2)
Solution: