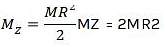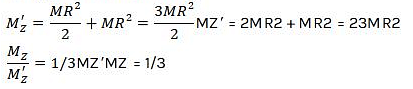JEE Main Previous year questions (2016-2024): Rotational Motion | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q.1. Solid sphere A is rotating about an axis PQ. If the radius of the sphere is 5 cm then its radius of gyration about PQ will be √x cm. The value of x is _______ [JEE Main 2023]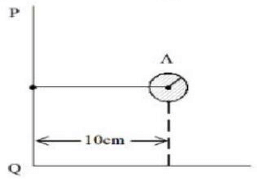
Ans. 110
Q.2. A body of mass 200 g is tied to a spring of spring constant 12.5 N/m, while the other end of spring is fixed at point O. If the body moves about O in a circular path on a smooth horizontal surface with constant angular speed 5rad/s. Then the ratio of extension in the spring to its natural length will be : [JEE Main 2023]
(a) 2:5
(b) 1: 1
(c) 2: 3
(d) 1: 2
Ans. c
Q.3. A uniform solid cylinder with radius R and length L has moment of inertia I1, about the axis of the cylinder. A concentric solid cylinder of radius R' = R/2 and length L' = L/2 is carved out of the original cylinder. If I2 is the moment of inertia of the carved out portion of the cylinder then I1/I2 = _______
(Both I1 and I2 are about the axis of the cylinder) [JEE Main 2023]
Ans. 32
Q.4. Four identical discs each of mass 'M' and diameter 'a' are arranged in a small plane as shown in figure. If the moment of inertia of the system about OO′ is x/4Ma2. Then, the value of x will be ____________. [JEE Main 2022]
Ans. (3)
Q.5. A solid cylinder length is suspended symmetrically through two massless strings, as shown in the figure. The distance from the initial rest position, the cylinder should be unbinding the strings to achieve a speed of 4 ms−1, is ____________ cm. (take g = 10 ms−2
[JEE Main 2022]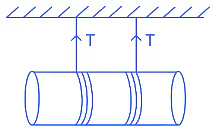
Ans. (120)

16 = 40 / 3 × s ⇒ s =0.3 × 4 = 120 cm
Q.6. A pulley of radius 1.5 m is rotated about its axis by a force F= (12t − 3t2)N applied tangentially (while t is measured in seconds). If moment of inertia of the pulley about its axis of rotation is 4.5 kg m2, the number of rotations made by the pulley before its direction of motion is reversed, will be K / π. The value of K is ___________. [JEE Main 2022]
Ans. (18)
t = 6 sec
Q.7. The radius of gyration of a cylindrical rod about an axis of rotation perpendicular to its length and passing through the center will be ___________ m. [JEE Main 2022]
Given, the length of the rod is 10√3 m.
Ans. (5)
Q.8. A disc of mass 1 kg and radius R is free to rotate about a horizontal axis passing through its centre and perpendicular to the plane of disc. A body of same mass as that of disc is fixed at the highest point of the disc. Now the system is released, when the body comes to the lowest position, its angular speed will be 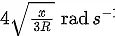 where x= ____________. (g = 10 ms-2) [JEE Main 2022]
where x= ____________. (g = 10 ms-2) [JEE Main 2022]
Ans. (5)
Loss in P.E. = Gain in K.E.
Q.9. Three identical spheres each of mass M are placed at the corners of a right angled triangle with mutually perpendicular sides equal to 3 m each. Taking point of intersection of mutually perpendicular sides as origin, the magnitude of position vector of centre of mass of the system will be √x m. The value of x is ____________. [JEE Main 2022]
Ans. (2)
x = 2
Q.10. Four particles with a mass of 1 kg, 2 kg, 3 kg and 4 kg are situated at the corners of a square with side 1 m (as shown in the figure). The moment of inertia of the system, about an axis passing through the point O and perpendicular to the plane of the square, is ______________ kg m2. [JEE Main 2022]
Ans. (5)
Q.11. Moment of Inertia (M.I.) of four bodies having same mass 'M' and radius '2R' are as follows: [JEE Main 2022]
I1 = M.I. of solid sphere about its diameter
I2 = M.I. of solid cylinder about its axis
I3 = M.I. of solid circular disc about its diameter
I4 = M.I. of thin circular ring about its diameter
If 2(I2 + I3) + I4 = x . I1, then the value of x will be __________.
Ans. (5)
⇒ x = 5
Q.12. The moment of inertia of a uniform thin rod about a perpendicular axis passing through one end is I1. The same rod is bent into a ring and its moment of inertia about a diameter is I2. If I1 / I2 is xπ2 / 3, then the value of x will be ____________. [JEE Main 2022]
Ans. (8)
Q.13. A solid cylinder and a solid sphere, having same mass M and radius R, roll down the same inclined plane from top without slipping. They start from rest. The ratio of velocity of the solid cylinder to that of the solid sphere, with which they reach the ground, will be :
[JEE Main 2022]
(a) 
(b) 
(c) 
(d) 
Ans. (d)
Q.14. A disc with a flat small bottom beaker placed on it at a distance R from its center is revolving about an axis passing through the center and perpendicular to its plane with an angular velocity ω. The coefficient of static friction between the bottom of the beaker and the surface of the disc is μ. The beaker will revolve with the disc if : [JEE Main 2022]
(a) 
(b) 
(c) 
(d) 
Ans. (b)
To move together
Q.15. A solid spherical ball is rolling on a frictionless horizontal plane surface about its axis of symmetry. The ratio of rotational kinetic energy of the ball to its total kinetic energy is [JEE Main 2022]
(a) 2/5
(b) 2/7
(c) 1/5
(d) 7/10
Ans. (b)
Q.16. A thin circular ring of mass M and radius R is rotating with a constant angular velocity 2 rads−1 in a horizontal plane about an axis vertical to its plane and passing through the center of the ring. If two objects each of mass m be attached gently to the opposite ends of a diameter of ring, the ring will then rotate with an angular velocity (in rads−1)
[JEE Main 2022]
(a) 
(b) 
(c) 
(d) 
Ans. (c)
Q.17. One end of a massless spring of spring constant k and natural length l0 is fixed while the other end is connected to a small object of mass m lying on a frictionless table. The spring remains horizontal on the table. If the object is made to rotate at an angular velocity ω about an axis passing through fixed end, then the elongation of the spring will be : [JEE Main 2022]
(a) 
(b) 
(c) 
(d) 
Ans. (c)
Q.18. When a ball is dropped into a lake from a height 4.9 m above the water level, it hits the water with a velocity v and then sinks to the bottom with the constant velocity v. It reaches the bottom of the lake 4.0 s after it is dropped. The approximate depth of the lake is :
[JEE Main 2022]
(a) 19.6 m
(b) 29.4 m
(c) 39.2 m
(d) 73.5 m
Ans. (b)
∴ depth = 9.8 × 3 = 29.4 m
Q.19. Match List-I with List-II [JEE Main 2022]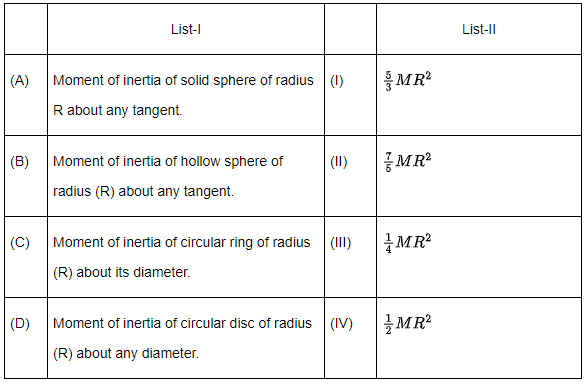 Choose the correct answer from the options given below :
Choose the correct answer from the options given below :
(a) A - II, B - I, C - IV, D - III
(b) A - I, B - II, C - IV, D - III
(c) A - II, B - I, C - III, D - IV
(d) A - I, B - II, C - III, D - IV
Ans. (a)
(A) Moment of inertia of solid sphere of radius R about a tangent
=
⇒ A − (II)
(B) Moment of inertia of hollow sphere of radius R about a tangent
=
⇒ B − (I)
(C) Moment of inertia of circular ring of radius (R) about its diameter = (MR2) / 2
⇒ C − (IV)
(D) Moment of inertia of circular disc of radius (R) about any diameter
=
⇒ D − (III)
Q.20. A ball is spun with angular acceleration α = 6t2 − 2t where t is in second and α is in rads−2. At t = 0, the ball has angular velocity of 10 rads−1 and angular position of 4 rad. The most appropriate expression for the angular position of the ball is : [JEE Main 2022]
(a) 
(b) 
(c) 
(d) 
Ans. (b)
Q.21. A spherical shell of 1 kg mass and radius R is rolling with angular speed ω on horizontal plane (as shown in figure). The magnitude of angular momentum of the shell about the origin O is a / 3 R2ω. The value of a will be : [JEE Main 2022]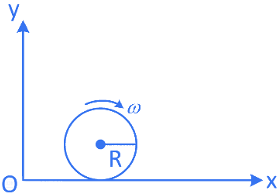 (a) 2
(a) 2
(b) 3
(c) 5
(d) 4
Ans. (c)
⇒ a = 5
Q.22. A flat surface of a thin uniform disk A of radius R is glued to a horizontal table. Another thin uniform disk B of mass M and with the same radius R rolls without slipping on the circumference of A, as shown in the figure. A flat surface of B also lies on the plane of the table. The center of mass of B has fixed angular speed ω about the vertical axis passing through the center of A. The angular momentum of B is nMωR2 with respect to the center of A. Which of the following is the value of n ? [JEE Advance 2022] (a) 2
(a) 2
(b) 5
(c) 7/2
(d) 9/2
Ans. (b)
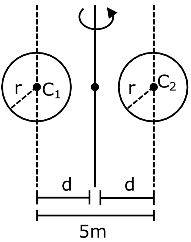
Q.23. A system consists of two identical spheres each of mass 1.5 kg and radius 50 cm at the end of light rod. The distance between the centres of the two spheres is 5 m. What will be the moment of inertia of the system about an axis perpendicular to the rod passing through its midpoint? [JEE Main 2021]
(a) 18.75 kgm2
(b) 1.905 × 105 kgm2
(c) 19.05 kgm2
(d) 1.875 × 105 kgm2
Ans. (c)
M = 1.5 kg, r = 0.5 m, d = 5/2 mI
= 2(25Mr2 + Md2)
= 19.05 kgm2
Q.24. Two discs have moments of inertia I1 and I2 about their respective axes perpendicular to the plane and passing through the centre. They are rotating with angular speeds, ω1 and ω2 respectively and are brought into contact face to face with their axes of rotation coaxial. The loss in kinetic energy of the system in the process is given by : [JEE Main 2021]
(a) 
(b) 
(c) 
(d) 
Ans. (c)
From conservation of angular momentum we get
Solving above we get
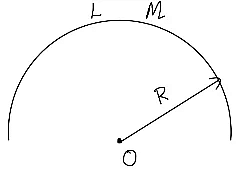
Q.25. A huge circular arc of length 4.4 ly subtends an angle '4s' at the centre of the circle. How long it would take for a body to complete 4 revolution if its speed is 8 AU per second?
[JEE Main 2021]
Given : 1 ly = 9.46 × 1015 m
1 AU = 1.5 × 1011 m
(a) 4.1 × 108 s
(b) 4.5 × 1010 s
(c) 3.5 × 106 s
(d) 7.2 × 108 s
Ans. (b)
R = l / θ
Time =
put l = 4.4 × 9.46 × 1015
v = 8 × 1.5 × 1011
we get time = 4.5 × 1010 sec.
Q.26. The solid cylinder of length 80 cm and mass M has a radius of 20 cm. Calculate the density of the material used if the moment of inertia of the cylinder about an axis CD parallel to AB as shown in figure is 2.7 kg m2. [JEE Main 2021]
(a) 14.9 kg/m3
(b) 7.5 × 101 kg/m3
(c) 7.5 × 102 kg/m3
(d) 1.49 × 102 kg/m3
Ans. (d)
Parallel axis theorem
M = 15 kg
⇒
= 0.1492 × 103
Q.27. Given below are two statements : one is labelled as Assertion A and the other is labelled as Reason R. [JEE Main 2021]
Assertion A : Moment of inertia of a circular disc of mass 'M' and radius 'R' about X, Y axes (passing through its plane) and Z-axis which is perpendicular to its plane were found to be Ix, Iy and Iz respectively. The respectively radii of gyration about all the three axes will be the same.
Reason R : A rigid body making rotational motion has fixed mass and shape. In the light of the above statements, choose the most appropriate answer from the options given below :
(a) Both A and R are correct but R is NOT the correct explanation of A.
(b) A is not correct but R is correct.
(c) A is correct but R is not correct.
(d) Both A and R are correct and R is the correct explanation of A.
Ans. (b)
Iz = Ix + Iy (using perpendicular axis theorem) & I = mk2 (K : radius of gyration)
so, mKz2 = mKx2 + mKy2
Kz2 = Kx2 + Ky2
so radius of gyration about axes x, y & z won't be same hence assertion A is not correct reason R is correct statement (property of a rigid body)
Q.28. Consider a situation in which a ring, a solid cylinder and a solid sphere roll down on the same inclined plane without slipping. Assume that they start rolling from rest and having identical diameter. [JEE Main 2021]
The correct statement for this situation is
(a) All of them will have same velocity.
(b) The ring has greatest and the cylinder has the least velocity of the centre of mass at the bottom of the inclined plane.
(c) The sphere has the greatest and the ring has the least velocity of the centre of mass at the bottom of the inclined plane.
(d) The cylinder has the greatest and the sphere has the least velocity of the centre of mass at the bottom of the inclined plane.
Ans. (c)
ICM is maximum for ring.
⇒ v is least for ring.
Q.29. A body rolls down an inclined plane without slipping. The kinetic energy of rotation is 50% of its translational kinetic energy. The body is : [JEE Main 2021]
(a) Solid sphere
(b) Solid cylinder
(c) Hollow cylinder
(d) Ring
Ans. (b)
Body is solid cylinder
Q.30. Consider a uniform wire of mass M and length L. It is bent into a semicircle. Its moment of inertia about a line perpendicular to the plane of the wire passing through the center is :
[JEE Main 2021]
(a) 
(b) 
(c) 
(d) 
Ans. (d)
∴ From figure,
L = πR
⇒ R = L / π
Moment of inertia about center O,
Q.31. A particle of mass m moves in a circular orbit under the central potential field, U(r)=−C/r, where C is a positive constant. The correct radius − velocity graph of the particle's motion is : [JEE Main 2021]
(a)
(b)
(c)
(d)
Ans. (b)
Given potential field U(r) = -C/r
∴ the graph between r & v will be hyperbolic.
Q.32. A thin circular ring of mass M and radius r is rotating about its axis with an angular speed ω. Two particles having mass m each are now attached at diametrically opposite points. The angular speed of the ring will become : [JEE Main 2021]
(a) 
(b) 
(c) 
(d) 
Ans. (c)
τnet = 0, so angular momentum is conserved
By angular momentum conservation
Iiωi = Ifωf
(MR2)ω = (MR2 + 2mR2)ωf
Q.33. A mass M hangs on a massless rod of length l which rotates at a constant angular frequency. The mass M moves with steady speed in a circular path of constant radius. Assume that the system is in steady circular motion with constant angular velocity ω. The angular momentum of M about point A is LA which lies in the positive z direction and the angular momentum of M about point B is LB. The correct statement for this system is :
[JEE Main 2021]
(a) LA is constant, both in magnitude and direction
(b) LB is constant in direction with varying magnitude
(c) LB is constant, both in magnitude and direction
(d) LA and LB are both constant in magnitude and direction
Ans. (a)
Net force on M is towards A, hence torque is zero about A.
as r ⊥ p so LA = constant
Q.34. The maximum and minimum distances of a comet from the Sun are 1.6 × 1012 m and 8.0 × 1010 m respectively. If the speed of the comet at the nearest point is 6 × 104 ms−1, the speed at the farthest point is : [JEE Main 2021]
(a) 3.0 × 103 m/s
(b) 6.0 × 103 m/s
(c) 1.5 × 103 m/s
(d) 4.5 × 103 m/s
Ans. (a)
v1 = 6 × 104 m/s
Let point 1 is nearest point,
and point 2 is farthest point.
Given, r1 = 8 × 1010 m & r2 = 1.6 × 1012 m
By angular momentum conservation
L1 = L2
mr1v1 = mr2v2
⇒ v2 = 3.0 × 103 m/s
Q.35. A block of 200 g mass moves with a uniform speed in a horizontal circular groove, with vertical side walls of radius 20 cm. If the block takes 40 s to complete one round, the normal force by the side walls of the groove is : [JEE Main 2021]
(a) 9.859 × 10−2 N
(b) 0.0314 N
(c) 9.859 × 10−4 N
(d) 6.28 × 10−3 N
Ans. (c)
Normal force will provide the necessary centripetal force.
⇒ N = mω2R
Also, ω = 2πt
∴ N = 9.859 × 10−4 N
Q.36. A cord is wound round the circumference of wheel of radius r. The axis of the wheel is horizontal and the moment of inertia about it is I. A weight mg is attached to the cord at the end. The weight falls from rest. After falling through a distance 'h', the square of angular velocity of wheel will be : [JEE Main 2021]
(a) 
(b) 
(c) 2gh
(d) 
Ans. (b)
Using energy conservation between A and B point
Q.37. A particle is moving with uniform speed along the circumference of a circle of radius R under the action of a central fictitious force F which is inversely proportional to R3. Its time period of revolution will be given by : [JEE Main 2021]
(a) T∝R4/3
(b) T∝R5/2
(c) T∝R3/2
(d) T∝R2
Ans. (d)
T∝R2
Q.38. Four identical solid spheres each of mass 'm' and radius 'a' are placed with their centres on the four corners of a square of side 'b'. The moment of inertia of the system about one side of square where the axis of rotation is parallel to the plane of the square is : [JEE Main 2021]
(a) 4 / 5ma2
(b) 8 / 5ma2 + mb2
(c) 4 / 5ma2 + 2mb2
(d) 8 / 5ma2 + 2mb2
Ans. (d)
Q.39. A sphere of radius 'a' and mass 'm' rolls along a horizontal plane with constant speed v0. It encounters an inclined plane at angle θ and climbs upward. Assuming that it rolls without slipping, how far up the sphere will travel? [JEE Main 2021]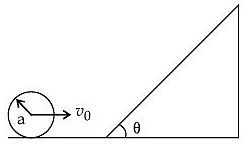 (a)
(a) 
(b) 
(c) 
(d) 
Ans. (b)
From energy conservation
from triangle, sinθ = h / l
then h = l sinθ
Q.40. A circular hole of radius (a / 2) is cut out of a circular disc of radius 'a' as shown in figure. The centroid of the remaining circular portion with respect to point 'O' will be :
[JEE Main 2021]
(a) 1 / 6a
(b) 2 / 3a
(c) 5 / 6a
(d) 10 / 11a
Ans. (c)
Let σ is the surface mass density of disc.
Q.41. Moment of inertia (M. I.) of four bodies, having same mass and radius, are reported as;
I1 = M.I. of thin circular ring about its diameter, [JEE Main 2021]
I2 = M.I. of circular disc about an axis perpendicular to disc and going through the centre,
I3 = M.I. of solid cylinder about its axis and
I4 = M.I. of solid sphere about its diameter.
Then :
I1 = I2 = I3 > I4
I1 + I3 < I2 + I4
I1 = I2 = I3 < I4
I1 + I2 = I3 + 5 /2 I4
Ans. (a)
Let M and R be the mass and radius of four bodies. Then, as per question, their moment of inertia are
∴ I1 = I2 = I3 > I4
Q.42. A 2 kg steel rod of length 0.6 m is clamped on a table vertically at its lower end and is free to rotate in vertical plane. The upper end is pushed so that the rod falls under gravity, ignoring the friction due to clamping at its lower end, the speed of the free end of rod when it passes through its lowest position is ____________ ms−1. (Take g = 10 ms−2) [JEE Main 2021]
Ans. (6)
by energy conservation
⇒
As we know the relation between the linear speed and angular speed,Hence, the speed of the free end of the rod when it passes through its lowest position is 6 m/s.
Q.43. In the given figure, two wheels P and Q are connected by a belt B. The radius of P is three times as that of Q. In case of same rotational kinetic energy, the ratio of rotational inertias (I1 / I2) will be x : 1. The value of x will be _____________. [JEE Main 2021]
Ans. (9)
Q.44. A solid disc of radius 20 cm and mass 10 kg is rotating with an angular velocity of 600 rpm, about an axis normal to its circular plane and passing through its centre of mass. The retarding torque required to bring the disc at rest in 10 s is ____________ π × 10−1 Nm.
[JEE Main 2021]
Ans. (4)
Q.45. The following bodies, [JEE Main 2021]
(1) a ring
(2) a disc
(3) a solid cylinder
(4) a solid sphere,
of same mass 'm' and radius 'R' are allowed to roll down without slipping simultaneously from the top of the inclined plane. The body which will reach first at the bottom of the inclined plane is ___________. [Mark the body as per their respective numbering given in the question]
Ans. (4)
solid sphere will take minimum time.
Q.46. The angular speed of truck wheel is increased from 900 rpm to 2460 rpm in 26 seconds. The number of revolutions by the truck engine during this time is _____________. (Assuming the acceleration to be uniform). [JEE Main 2021]
Ans. (728)
= 2 π rad/sec2
= 728
Q.47. A solid disc of radius 'a' and mass 'm' rolls down without slipping on an inclined plane making an angle θ with the horizontal. The acceleration of the disc will be 2/bg sinθ where b is ____________. (Round off to the Nearest Integer) (g = acceleration due to gravity, θ = angle as shown in figure) [JEE Main 2021]
Ans. (3)
We know that, on an inclined plane
Acceleration,
As per question, acceleration of the disc will be 2/bgsinθ.
Comparing it with Eq. (i), we get
b = 3
Q.48. Consider a 20 kg uniform circular disk of radius 0.2 m. It is pin supported at its center and is at rest initially. The disk is acted upon by a constant force F = 20 N through a massless string wrapped around is periphery as shown in the figure. [JEE Main 2021] Suppose the disk makes n number of revolutions to attain an angular speed of 50 rad s−1.
Suppose the disk makes n number of revolutions to attain an angular speed of 50 rad s−1.
The value of n, to the nearest integer, is __________.
[Given : In one complete revolution, the disk rotates by 6.28 rad]
Ans. (20)
of revolution =125 / 2π ≈ 20 revolution
Q.49. A small bob tied at one end of a thin string of length 1 m is describing a vertical circle so that the maximum and minimum tension in the string are in the ratio 5 : 1. The velocity of the bob at the highest position is ________ m/s. (Take g = 10 m/s2) [JEE Main 2021]
Ans. (5)
Let the speed of bob at lowest position be v1 and at the highest position be v2.
Maximum tension is at lowest position and minimum tension is at the highest position. Now, using, conservation of mechanical energy,
⇒v22= 25 ⇒ v2 = 5 m/s
Thus, velocity of bob at highest position 5 m/s.
Q.50. A uniform thin bar of mass 6 kg and length 2.4 meter is bent to make an equilateral hexagon. The moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of hexagon is _______ × 10−1 kg m2. [JEE Main 2021]
Ans. (8)
MOI of AB about
MOI of AB about O,
= 0.8 kgm2
= 8 × 10−1 kg-m2
Q.51. As shown in the figure, a bob of mass m is tied by a massless string whose other end portion is wound on a fly wheel (disc) of radius r and mass m. When released from rest, the bob starts falling vertically. When it has covered a distance of h, the angular speed of the wheel will be [2020]

Ans: (1)
Given, block of mass is suspended from a pulley.
When system is released, potential energy is converted into kinetic energy.
So, Potential energy = Translational Kinetic energy + Rotational Kinetic energy
Where m is mass of the block, v is velocity of the block, I is moment of inertia, ω is angular velocity
Moment of inertia is given by
I = 1/2 mr2
And ω = v/r
⇒ v = ωr
So,
Q.52. Three point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle of sides 4.0 cm, 3.0 cm and 5.0 cm respectively as shown in the figure. The centre of mass of the system is at a point [2020]
(a) 0.6 cm right and 2.0 cm above 1 kg mass
(b) 1.5 cm right and 1.2 cm above 1 kg mass
(c) 2.0 cm right and 0.9 cm above 1 kg mass
(d) 0.9 cm right and 2.0 cm above 1 kg mass
Ans: (d)
Let mass be situated at point A, B and C and point A is at origin.
We know that, centre of mass is given by
and
So,
And
=2.5/5 = 2m
So, the center of mass of the system is 0.9 cm right and 2.0 cm above 1 kg mass.
Q.53. The radius of gyration of a uniform rod of length l, about an axis passing through a point l/4 away from the centre of the rod, and perpendicular to it, is [2020]
Ans: (3)
The radius of gyration is defined as,
I = mK2 ...(1)
Where I is moment of inertia, m is mass and K is radius of gyration. For given rod, moment of inertia is
From Eq. (1), we have
Q.54. Mass per unit area of a circular disc of radius a depends on the distance r from its centre as σ(r) = A + Br. The moment of inertia of the disc about the axis, perpendicular to the plane and passing through its centre is [2020]
Ans: (1)
Given that
σ(r) = A + Br (1)
Moment of inertia is given by
here dm = σ2πrdr
So,
From Eq. (1) we get,
Q.55. The coordinates of centre of mass of a uniform flag shaped lamina (thin flat plate) of mass 4 kg are (The coordinates of the same are shown in figure) are [2020]
(a) (1.25 m, 1.50 m)
(b) (0.75 m, 1.75 m)
(c) (0.75 m, 0.75 m)
(d) (1 m, 1.75 m)
Ans: (b)
Let divide flag shaped plate into two plates, named as plate 1 and plate 2, as shown in the following figure
Let masses of plates 1 and 2 be m1 and m2 respectively
Since, mass is uniform. so, masses of divided plate are
m1 = 3 kg, m2 = 1 kg
Centre of mass of plate 1 is given by
Centre of mass of plate 2 is given by
Centre of mass of whole plate is given by
Q.56. A particle of mass m is fixed to one end of a light spring having force constant k and unstretched length l. The other end is fixed. The system is given an angular speed ω about the fixed end of the spring such that it rotates in a circle in gravity free space. Then the stretch in the spring is [2020]
Ans: (2)
Let the stretched length be x.
Energy on a particle in the system are:
Spring restore energy (kx)
Rotational kinetic energy (m/ω2 )
Rotational potential energy (mxω2)
From conservation of energy, we have
Q.57. Consider a uniform rod of mass M = 4 m and length l pivoted about its centre. A mass m moving with velocity v making angle θ = π/4 to the rod’s long axis collides with one end of the rod and sticks to it. The angular speed of the rod-mass system just after the collision is [2020]
Ans: (3)
Let the angular velocity of the system after collision be ω.
Since, uniform rod is heavier than the particle there is only rotational motion after collision. By conservation of angular momentum, we have
Li = Lf
Here If is the total final moment of inertia of the system, that is
So,
Q.58. A uniform sphere of mass 500 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is [2020]
(a) 8.75 × 10−4 J
(b) 8.75 × 10−3 J
(c) 6.25 × 10−4 J
(d) 1.13 × 10−3 J
Ans: (a)
Given that m = 500 g = 0.5 kg, v = 5 cm/s
For pure rolling total kinetic energy is given by
Translation kinetic energy + Rotational kinetic energy
We know that
So,
For uniform sphere, we have
So,
Q.59. As shown in figure when a spherical cavity (centred at O) of radius 1cm is cut out of a uniform sphere of radius R (centred at C), the centre of mass of remaining (shaded) part of sphere is at G, i.e. on the surface of the cavity, R can be determined by the equation [2020]
(a) (R2 + R + 1) (2 - R) = 1
(b) (R2 - R - 1) (2 - R) = 1
(c) (R2 - R + 1)(2 - R) = 1
(d) (R2 + R - 1) (2 - R) = 1
Ans: (a)
Lets take centre point C as references point. So,
Distance of point G (new centre of mass) from C (old centre of mass) is
CG = OG - OC
= 1- (R - 1)= 2 - R
Mass of the solid sphere is given by
M1 = 4πR3ρ/3
Mass of the cavity is given by
Centre of mass of the remaining sphere is
Q.60. Three solid spheres each of mass m and diameter d are stuck together such that the lines connecting the centres form an equilateral triangle of side of length d. The ratio I0/IA of moment of inertia I0 of the system about an axis passing the centroid and about center of any of the sphere IA and perpendicular to the plane of the triangle is [2020] (a) 13/23
(a) 13/23
(b) 15/13
(c) 23/13
(d) 13/15
Ans: a
Moment of inertia at point O is given by
Io = IAO + IBO + ICO
Since,
IAO = IBO = ICO
So, I0 = 3IAO
Moment of inertia due to one solid sphere at point O is given by using parallel axis theorem.
Therefore,
Q.61. One end of a straight uniform 1 m long bar is pivoted on horizontal table. It is released from rest when it makes an angle 30° from the horizontal (see figure). Its angular speed when it hits the table is given as √n rad/s. where n is an integer. The value n is _________.
Ans: 15
From conservation of mechanical energy, we have
Ui + Ki = Uf + Kf
Initially bar is at rest so initial kinetic energy is zero.
Similarly, when bar hit the table its final potential energy is zero.
So,
Ui = Kf
Initial potential energy is given by
Since, there is only circular motion so final kinetic energy is totally rotational kinetic energy, that is,
So,
Moment of inertia of bar on the axis of rotation from one end is given by
So,
⇒ ω = √15
Therefore, n = 15
Q.62. A uniformly thick wheel with moment of inertia I and radius R is free to rotate about its centre of mass (see figure). A massless string is wrapped over its rim and two blocks of masses m1 and m2 (m1 > m2) are attached to the ends of the string. The system is released from rest. The angular speed of the wheel when m1 descends by a distance h is

Ans: (1)
Since, there is no external force. Applying work energy theorem, we get
ΔU = ΔK
⇒ Uf - Ui = Kf - Ki
Change in potential energy is given by
ΔU = Uf - Ui = (m1 - m2)gh
Change in kinetic energy is given by
ΔK = (change in linear kinetic energy) + (change in rotational kinetic energy)
So,
Q.63. A rod of length L has non-uniform linear mass density given by ρ (x) = a + b (x/L)2 , where a and b are constants and 0 ≤ x ≤ L. The value of x for the centre of mass of the rod is at 
Ans: (2)
Let small mass element dm of length dx at distance x from one end.
Given that
So,
Centre of mass is given by
Q.64. An L-shaped object, made of thin rods of uniform mass density, is suspended with a string as shown in figure. If AB = BC, and the angle made by AB with downward vertical is θ, then: (2019) (a)
(a) 
(b) tan θ = 1/2
(c) 
(d) tan θ = 1/3
Ans: (d)
Let m be the mass of the rod and L be length of segment AB or BC.
So, AB = BC = L
Balancing torque about suspended point
Q.65. A rod of length 50 cm is pivoted at one end. It is raised such that if makes an angle of 30° from the horizontal as shown and released from rest. Its angular speed when it passes through the horizontal (in rad s−1) will be (g = 10 m/s2) (2019)
(a) 
(b) 
(b) 
(d) 
Ans: (b)
Let m be the mass of rod and ω be the angular speed.
Work done by gravity on rod from initial stale to final state.
According to work energy theorem
From Eq. (1) and (2), we get
Q.66. To mop-clean a floor, a cleaning machine presses a circular mop of radius R vertically down with a total force F and rotates it with a constant angular speed about its axis. If the force F is distributed uniformly over the mop and if coefficient of friction between the mop and the floor is μ, the torque applied by the machine on the mop is (2019)
(a) μFR/3
(b) μFR/6
(c) μFR/2
(d) 2/3 μFR
Ans: (d)
Consider a strip of r and thickness dr. Force for strip is given as
Integrating both the sides, we get
Q.67. A homogeneous solid cylindrical roller of radius R and mass M is pulled on a cricket pitch by a horizontal force. Assuming rolling without slipping, angular acceleration of the cylinder is (2019)
(a) 
(b) 
(c) 
(d) 
Ans: (d)
Relation between torque and moment of inertia
Q.68. Two identical spherical balls of mass M and radius R each are stuck on two ends of a rod of length 2R and mass M (see figure). The moment of inertia of the system about the axis passing perpendicularly through the center of the rod is (2019) (a)
(a) 
(b) 
(c) 
(d) 
Ans: (a)
Applying parallel axis theorem for ball
Moment of Inertia of two balls
Moment inertia of rod
Moment of inertia of whole system is
Q.69. A rigid massless rod of length 3l has two masses attached at each end as shown in the figure. The rod is pivoted at point P on the horizontal axis (see figure). When released from initial horizontal position, its instantaneous angular acceleration will be (2019)
(a) 
(b) 
(c) 
(d) 
Ans: (a)
we have,
Q.70. An equilateral triangle ABC is cut from a thin solid sheet of wood (see figure). D, E and F are the midpoints of its sides as shown and G is the center of the triangle. The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane of the triangle is I0. If the smaller triangle DEF is removed from ABC, the moment of inertia of the remaining figure about the same axis is I. Then (2019)
(a) 
(b) 
(c) 
(d) 
Ans: (a)
Suppose M is mass and l is side of larger triangle then, M/4 and l/2 will be the mass and side of smaller triangle.
Thus, moment of inertia is
Q.71. A slab is subjected to two forces  of same magnitude F as shown in the figure. Force
of same magnitude F as shown in the figure. Force  is in xy-plane while force F1 acts along z-axis at the point
is in xy-plane while force F1 acts along z-axis at the point  The moment of these forces about point O will be (2019)
The moment of these forces about point O will be (2019)
(a) 
(b) 
(c) 
(d) 
Ans: (a)
Moment of force is
Q.72. A circular disc D1 of mass M and radius R has two identical discs D2 and D3 of the same mass M and radius R attached rigidly at its opposite ends (see figure). The moment of inertia of the system about the axis OO', passing through the center of D1, as shown in the figure, will be (2019)
(a) MR2
(b) 3MR2
(c) 4/5 MR2
(d) 2/3 MR2
Ans: (b)
Moment of inertia of the system is
I = Moment of inertia of disc D2 + Moment of inertia of disc D3 + Moment of inertia of disc D1
Since, disc D2 and D3 are identical.
Q.73. The magnitude of torque on a particle of mass 1 kg is 2.5 N·m about the origin. If the force acting on it is 1 N, and the distance of the particle from the origin is 5 m, the angle between the force and the position vector is (in radians) (2019)
(a) π /6
(b) π /3
(c) π /8
(d) π /4
Ans: (a)
Q.74. A string is wound around a hollow cylinder of mass 5 kg and radius 0.5 m. If the string is now pulled with a horizontal force of 40 N, and the cylinder is rolling without slipping on a horizontal surface (see figure), then the angular acceleration of the cylinder will be (Neglect the mass and thickness of the string): (2019)
(a) 20 rad/s2
(b) 16 rad/s2
(c) 12 rad/s2
(d) 10 rad/s2
Ans: (b)
As we know that,
Q.75. The position vector of the center of mass  of an asymmetric uniform bar of negligible area of cross-section as shown in figure is (2019)
of an asymmetric uniform bar of negligible area of cross-section as shown in figure is (2019)
(a) 
(b) 
(c) 
(d) 
Ans: (a)
Q.76. Let the moment of inertia of a hollow cylinder of length 30 cm (inner radius 10 cm and outer radius 20 cm), about its axis be I. The radius of a thin cylinder of the same mass such that its moment of inertia about its axis is also I is (2019)
(a) 12 cm
(b) 16 cm
(c) 14 cm
(d) 18 cm
Ans: (b)
Moment of Inertia of Hollow sphere is[a = radius of inner cylinder, b = radius of outer cylinder]
Now, radius of gyration is
Q.77. The moment of inertia of a solid sphere, about an axis parallel to its diameter and at a distance of x from it, is I(x). Which one of the graphs represents the variation of I(x) with x correctly? (2019)
(a)
(b)
(c)
(d)
Ans: (d)
Moment of Inertia of hollow sphere
Q.78. Two particles A and B are moving on two concentric circles of radii R1 and R2 with equal angular speed ω. At t = 0, their positions and direction of motion are shown in the figure: 
The relative velocity  is given by (2019)
is given by (2019)
(a) 
(b) 
(c) 
(d) 
Ans: (c)
Both the particles rotating with same angular speed in opposite direction
After π/2 rotation their velocities will be
Q.79. Seven identical circular planar disks, each of mass M and radius R are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point P is: (2018)
(a) 
(b) 
(c) 
(d) 
Ans: (b)
Moment of inertia of each disc about the given axis is,
Q.80. From a uniform circular disc of radius R and mass 9 M, a small disc of radius R/3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is: (2018)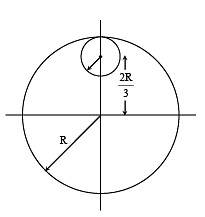 (a) 4MR2
(a) 4MR2
(b) 
(c) 10MR2
(d) 
Ans: (a)
Mass of disc = Volume x Density
9M = A x T x ρ (Area x thickness x density)
(i) Divided by (ii)
Moment of inertia of complete disc about an axis passes through O.
Moment of inertia of cut off disc about an axis passes through O
So, moment of inertia of remaining disc = I1 -I2
Q.81. A thin circular disk is in the xy plane as shown in the figure. The ratio of its moment of inertia about z and z' axes will be: (2018) (a) 1 : 4
(a) 1 : 4
(b) 1 : 5
(c) 1 : 3
(d) 1 : 2
Ans: (c)
We know that, the moment of inertia of the circular disk about the center is
Using parallel axis theorem,
Q.82. A uniform rod AB is suspended from a point X, at a variable distance x from A, as shown. To make the rod horizontal, a mass in is suspended from its end A. A set of (m, x) values is recorded. The appropriate variables that give a straight line, when plotted, are: (2018) (a)
(a) 
(b) m, x
(c) 
(d) m, x2
Ans: c
= y = mx + c
Q.83. A force of 40 N acts on a point B at the end of an L-shaped object, as shown in the figure. The angle θ that will produce maximum moment of the force about point A is given by (2018) (a) tanθ = 1/4
(a) tanθ = 1/4
(b) tanθ = 2
(c) tanθ = 1/2
(d) tan θ = 4
Ans: c
τA = f cosθ(4) + Fsinθ(2)
τA = 2F(sinθ + 2cosθ)
dτA/dθ = 2F[cosθ − 2sinθ] = 0
Tan θ = 1/2
Q.84. The moment of inertia of a uniform cylinder of length ℓ and radius R about its perpendicular bisector is I. What is the ratio ℓ /R such that the moment of inertia is minimum? (2017)
(a) 1
(b) 3√2
(c) 
(d) 
Ans: (c)
Q.85. A slender uniform rod of mass M and length l is pivoted at one end so that it can rotate in a vertical plane (see figure). There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle θ with the vertical is (2017)
(a) 
(b) 
(c) 
(d) 
Ans: (c)
Torque at angle θ
Q.86. Moment of inertia of an equilateral triangular lamina ABC, about the axis passing through its centre O and perpendicular to its plane is I0 as shown in the figure. A cavithy DEF is cut out from the lamina, where D,E,F are the mid points of the sides. Moment of inertia of the remaining part of lamina about the same axis is- (2017)




Ans: (1)
Q.87. In a physical balance working on the principle of moments, when 5 mg weight is placed on the left pan, the beam becomes horizontal. Both the empty pans of the balance are of equal mass. Which of the following statements is correct ? (2017)
(a) Every object that is weighted using this balance appears lighter than its actual weight
(b) Left arm is shorter than the right arm
(c) Both the arms are of same length
(d) Left arm is longer than the right arm
Ans: (b)
F1d1=F2d2
Consider mass of pan be m,as the mass of the pan is same initially, so when the weight is not placed on the pan the force acting will be same as mg on both sides,
∴ After the weight is placed on left pan,
(5mg+mg)d1=mgd2
d2=6d1
Hence the left arm (in which 5mg was placed) is shorter than right arm.
Q.88. A circular hole of radius R/4 is made in a thin uniform disc having mass M and radius R, as shown in figure. The moment of inertia of the remaining portion of the disc about an axis passing through the point O and perpendicular to the plane of the disc is- (2017)




Ans: (2)
Q.89. A roller is made by joining together two cones at their vertices O. It is kept on two rails AB and CD which are placed asymmetrically (see figure), with its axis perpendicular to CD and its centre O at the centre of line joining AB and CD (see figure). It is given a light push so that it starts rolling with its centre O moving parallel to CD in the direction shown. As it moves, the roller will tend to: (2016)
(a) turn left
(b) turn right
(c) go straight
(d) turn left and right alternately
Ans: (a)
If we take ‘r’ as the distance of IAOR from the axis of rotation, then ‘r’ decreases on left side as the object moves forward.
So, for left v = ωr' < ωr (for right point)
So, the roller will turn to the left as it moves forward.
Q.90. A cubical block of side 30cm is moving with velocity 2ms-1 on a smooth horizontal surface. The surface has a bump at a point O as shown in figure. The angular velocity (in rad/s) of the block immediately after it hits the bump, is: (2016) (a) 9.4
(a) 9.4
(b) 6.7
(c) 5.0
(d) 13.3
Ans: (c)
Using conservation of angular momentum
|
347 docs|185 tests
|
FAQs on JEE Main Previous year questions (2016-2024): Rotational Motion - 35 Years Chapter wise Previous Year Solved Papers for JEE
| 1. What is rotational motion in the context of JEE Main? |  |
| 2. How can I calculate angular velocity in rotational motion? |  |
| 3. What is the moment of inertia in rotational motion? |  |
| 4. How does torque affect rotational motion? |  |
| 5. Can you explain the concept of angular acceleration in rotational motion? |  |
|
347 docs|185 tests
|

|
Explore Courses for JEE exam
|

|



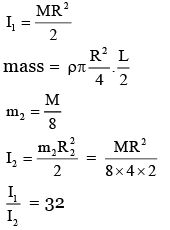

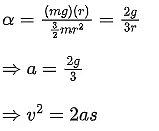



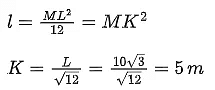











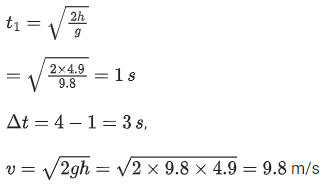





 M = 1.5 kg, r = 0.5 m, d = 5/2 mI
M = 1.5 kg, r = 0.5 m, d = 5/2 mI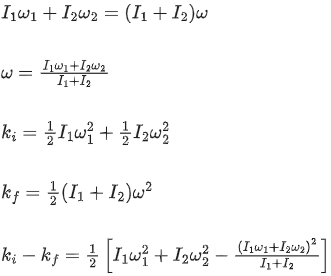







 ∴ From figure,
∴ From figure,















 by energy conservation
by energy conservation 

 Hence, the speed of the free end of the rod when it passes through its lowest position is 6 m/s.
Hence, the speed of the free end of the rod when it passes through its lowest position is 6 m/s.








 Let the speed of bob at lowest position be v1 and at the highest position be v2.
Let the speed of bob at lowest position be v1 and at the highest position be v2.

 MOI of AB about
MOI of AB about




















































































 [a = radius of inner cylinder, b = radius of outer cylinder]
[a = radius of inner cylinder, b = radius of outer cylinder]