JEE Main Previous year questions (2021-22): Differentiation | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q.1. Let 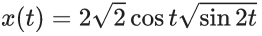 and
and 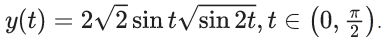 Then
Then 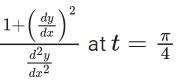 is equal to : (JEE Main 2022)
is equal to : (JEE Main 2022)
(a) 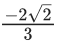
(b) 2/3
(c) 1/3
(d) (-2)/3
Ans. d
Q.2. The value of loge2(d/dx)(logcosxcosecx) at x = π/4 is (JEE Main 2022)
(a) -2/√2
(b) 2√2
(c) -4
(d) 4
Ans. d
Let f(x) = logcosxcos ec x
at x = π/4
∴ loge2f′(x) at x = π/4 = 4
Q.3. If y = tan−1(secx3 − tanx3) ,π/2 < x3 < 3π/2, then (JEE Main 2022)
(a) xy″ + 2y′ = 0
(b) x2y″ − 6y + (3π/2) = 0
(c) x2y″ − 6y + 3π = 0
(d) xy″−4y′ = 0
Ans. b
∴ y = tan-1(secθ - tanθ)
y" = -3x
Q.4. If cos−1(y/2) = loge(x/5)5, |y| < 2, then : (JEE Main 2022)
(a) x2y″ + xy′ − 25y = 0
(b) x2y″ − xy′ − 25y = 0
(c) x2y″ − xy′ + 25y = 0
(d) x2y″ + xy′ + 25y = 0
Ans. d
Differentiating on both side
Square on both side
Diff on both side
2xy′2 + 2y′y″x2 = −25 × 2yy′
xy' + y"x2 + 25y = 0
Q.5. Let f : R → R be a function defined by f(x) = 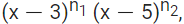 n1, n2 ∈ N. Then, which of the following is NOT true? (JEE Main 2022)
n1, n2 ∈ N. Then, which of the following is NOT true? (JEE Main 2022)
(a) For n1 = 3, n2 = 4, there exists α ∈ (3, 5) where f attains local maxima.
(b) For n1 = 4, n2 = 3, there exists α ∈ (3, 5) where f attains local minima.
(c) For n1 = 3, n2 = 5, there exists α ∈ (3, 5) where f attains local maxima.
(d) For n1 = 4, n2 = 6, there exists α ∈ (3, 5) where f attains local maxima.
Ans. c
Given,
f(x) =
Differentiating both side with respect to x, we get
Option A :
When n1 = 3 and n2 = 4 then
f′(x) = (x−3)3−1 (x−5)4−1 [3(x−5) + 4(x−3)]
= (x − 3)2(x − 5)3(7x − 27)
Critical point is at x = 3, 5 and 27/7
When value of f'(x) is less than (27/5), f'(x) is positive means slope of f(x) graph is positive.
And when value of f'(x) is greater than (27/7) but less than 5 then f'(x) is negative means slope of f(x) is negative.
So at (27/7) between 3 and 5, f(x) attain local maxima.
∴ Option A is correct.
Option B :
When n1 = 4 and n2 = 3 then
f′(x) = (x−3)4−1(x−5)3−1[4(x−5) + 3(x−3)]
= (x−3)3(x−5)2(7x−29)
Critical point is at x = 3, 5 and 29/7
When f'(x) is less than 29/7 but greater than 3 then f'(x) is negative means slope of graph of f(x) is negative.
And when f'(x) is greater than 29/7 but less than 5 then f'(x) is positive means slope of graph of f(x) is positive.
So at 29/7 between 3 and 5, f(x) attain local minima.
∴ Option (B) is correct.
Option C :
When n1 = 3 and n2 = 5 then
f′(x) = (x−3)3−1 (x−5)5−1 [3(x−5) + 5(x−3)]
= (x−3)2 (x−5)4 (8x−30)
Critical point is at x = 3, 5 and
When f'(x) is less than (30/8) but greater than 3 then f'(x) is negative means slope of graph of f(x) is negative.
And when f'(x) is greater than (30/8) but less than 5 then f'(x) is positive means slope of graph of f(x) is positive.
So, at (30/8) between 3 and 5, f(x) attain local minima.
∴ Option C is not true.
Similarly you can check option D also.
Q.6. Let 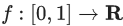 be a twice differentiable function in (0, 1) such that f(0) = 3 and f(1) = 5. If the line y = 2x + 3 intersects the graph of f at only two distinct points in (0, 1), then the least number of points x ∈ (0, 1), at which f′′(x) = 0, is _____. (JEE Main 2022)
be a twice differentiable function in (0, 1) such that f(0) = 3 and f(1) = 5. If the line y = 2x + 3 intersects the graph of f at only two distinct points in (0, 1), then the least number of points x ∈ (0, 1), at which f′′(x) = 0, is _____. (JEE Main 2022)
Ans. 2
If a graph cuts y = 2x + 5 in (0, 1) twice then its concavity changes twice.
∴ f′(x) = 0 at at least two points.
Q.7. Let 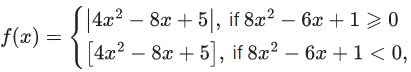 where [α] denotes the greatest integer less than or equal to α. Then the number of points
where [α] denotes the greatest integer less than or equal to α. Then the number of points 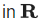 where f is not differentiable is ___________. (JEE Main 2022)
where f is not differentiable is ___________. (JEE Main 2022)
Ans. 3
∴ Non-diff at x = 1/4,
Q.8. If y(x) = (xx)x, x > 0, then (d2x/dy2) + 20 at x = 1 is equal to _____. (JEE Main 2022)
Ans. 16
Q.9. Let f and g be twice differentiable even functions on (−2, 2) such that f(1/4) = 0, f(1/2) = 0, f(1) = 1 and g(3/4) = 0, g(1) = 2. Then, the minimum number of solutions of f(x)g″(x) + f′(x)g′(x) = 0 in (−2,2) is equal to ________. (JEE Main 2022)
Ans. 4
Q.10. The function f(x) = x3 − 6x2 + ax + b is such that f(2) = f(4) = 0. Consider two statements:
Statement 1 : there exists x1, x2 ∈(2, 4), x1 < x2, such that f'(x1) = −1 and f'(x2) = 0.
Statement 2 : there exists x3, x4 ∈ (2, 4), x3 < x4, such that f is decreasing in (2, x4), increasing in (x4, 4) and 2f′(x3) = √3f(x4).
Then (JEE Main 2021)
(a) both Statement 1 and Statement 2 are true
(b) Statement 1 is false and Statement 2 is true
(c) both Statement 1 and Statement 2 are false
(d) Statement 1 is true and Statement 2 is false
Ans. a
f(x) = x3 − 6x2 + ax + b
f(2) = 8 − 24 + 2a + b = 0
2a + b = 16 .... (1)
f(4) = 64 − 96 + 4a + b = 0
4a + b = 32 .... (2)
Solving (1) and (2)
a = 8, b = 0
f(x) = x3 − 6x2 + 8x
f′(x) = 3x2 − 12x + 8
f″(x) = 6x− 12
⇒ f'(x) is ↑ for x > 2, and f'(x) is ↓ for x < 2
f′(2) = 12 − 24 + 8 = −4
f′(4) = 48 − 48 + 8 = 8
f′(x) = 3x2 − 12x + 8
vertex (2, −4)
f'(2) = −4, f'(4) = 8, f'(3) = 27 − 36 + 8
f'(x1) = −1, then x1 = 3
f'(x2) = 0
Again
f'(x) < 0 for x ∈ (2, x4)
f'(x) > 0 for x ∈ (x4, 4)
x4 ∈ (3, 4)
f(x) = x3 − 6x2 + 8x
f(3) = 27 − 54 + 24 = −3
f(4) = 64 − 96 + 32 = 0
For x4(3, 4)
f(x4) < −3√3
and f'(x3) > −4
2f'(x3) > −8
So, 2f'(x3) = √3 f(x4)
Correct Ans. (a).
Q.11. If 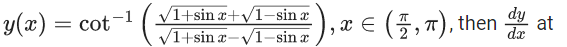 x = 5π/6 is: (JEE Main 2021)
x = 5π/6 is: (JEE Main 2021)
(a) -(1/2)
(b) -1
(c) 1/2
(d) 0
Ans. a
y'(x) = (-1)/2
Q.12. The local maximum value of the function 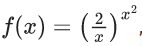 x > 0, is (JEE Main 2021)
x > 0, is (JEE Main 2021)
(a) (2√e)1/e
(b) (4/√e)e/4
(c) (e)2/e
(d) 1
Ans. c
LM = 2/√e
Local maximum value =
Q.13. Let A=[aij] be a 3 × 3 matrix, where 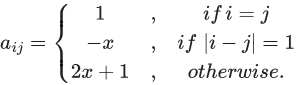
Let a function f : R → R be defined as f(x) = det(A). Then the sum of maximum and minimum values of f on R is equal to: (JEE Main 2021)
(a) -(20/27)
(b) 88/27
(c)20/27
(d) -(88/27)
Ans. d
|A| = 4x3 − 4x2 − 4x = f(x)
f′(x) = 4(3x2 − 2x − 1) = 0
⇒ x = 1; x = ((−1)/3)
∴ f(1) = −4; f(−(1/3)) = 20/27
Sum = -4 + (20/7) = -(88/27)
Q.14. If Rolle's theorem holds for the function f(x) = x3 − ax2 + bx − 4, x ∈ [1, 2] with f′(4/3) = 0, then ordered pair (a, b) is equal to : (JEE Main 2021)
(a) (−5, −8)
(b) (5, −8)
(c) (−5, 8)
(d) (5, 8)
Ans. d
f(1) = f(2)
⇒ 1 − a + b − 4 = 8 − 4a + 2b − 4
3a − b = 7 ..... (1)
f′(x) = 3x2 − 2ax + b
⇒ f′(4/3) = 0 ⇒ 3 × (16/9) − (8/3)a + b = 0
⇒ −8a + 3b = −16 ..... (2)
∴ a = 5, b = 8
Q.15. Let f be a twice differentiable function defined on R such that f(0) = 1, f'(0) = 2 and f'(x) ≠ 0 for all x ∈ R. If 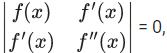 for all x ∈ R, then the value of f(1) lies in the interval : (JEE Main 2021)
for all x ∈ R, then the value of f(1) lies in the interval : (JEE Main 2021)
(a) (0, 3)
(b) (9, 12)
(c) (3, 6)
(d) (6, 9)
Ans. d
⇒ f(x).f″(x) − (f′(x))2 = 0
Dividing by (f(x))2, we get
Integrating both side,
⇒ 2/1 = c
⇒ c = 2
at x = 0,
ln|f(0)| = 0 + c′
⇒ 0 = 0 + c′
⇒ c′ = 0
∴ n|f(x)| = 2x
⇒ f(x) = e2x
f(1) = e2 = (2.71)2 = 7.34
So it lie between (6, 9).
Q.16. Let f(x) be a cubic polynomial with f(1) = −10, f(−1) = 6, and has a local minima at x = 1, and f'(x) has a local minima at x = −1. Then f(3) is equal to ____. (JEE Main 2021)
Ans. 22
Let f(x) = ax3 + bx2 + cx + d
f'(x) = 3ax2 + 2bx + c ⇒ f''(x) = 6ax + 2b
f'(x) has local minima at x = −1, so
∵ f''(−1) = 0 ⇒ −6a + 2b = 0 ⇒ b = 3a ..... (i)
f(x) has local minima at x = 1
f'(1) = 0
⇒ 3a + 6a + c = 0
⇒ c = −9a ..... (ii)
f(1) = −10
⇒ −5a + d = −10 ..... (iii)
f(−1) = 6
⇒ 11a + d = 6 ..... (iv)
Solving Eqs. (iii) and (iv)
a = 1, d = −5
From Eqs. (i) and (ii),
b = 3, c = −9
∴ f(x) = x3 + 3x2 − 9x − 5
So, f(3) = 27 + 27 − 27 − 5 = 22
Q.17. If 'R' is the least value of 'a' such that the function f(x) = x2 + ax + 1 is increasing on [1, 2] and 'S' is the greatest value of 'a' such that the function f(x) = x2 + ax + 1 is decreasing on [1, 2], then the value of |R − S| is _____. (JEE Main 2021)
Ans. 2
f(x) = x2 + ax + 1
f'(x) = 2x + a
when f(x) is increasing on [1, 2]
2x + a ≥ 0 ∀ x ∈ [1, 2]
a ≥ −2x ∀ x ∈ [1, 2]
R = −4
when f(x) is decreasing on [1, 2]
2x + a ≤ 0 ∀ x ∈ [1, 2]
a ≤ −2 ∀ x ∈ [1, 2]
S = −2
|R − S| = | −4 + 2 | = 2
Q.18. If y = y(x) is an implicit function of x such that loge(x + y) = 4xy, then 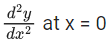 is equal to _____. (JEE Main 2021)
is equal to _____. (JEE Main 2021)
Ans. 40
ln(x + y) = 4xy (At x = 0, y = 1)
x + y = e4xy
⇒ 1 + (dy/dx) = e4xy(4x(dy/dx) + 4y)
At x = 0
dy/dx = 3
At x = 0, (d2y/dx2) = e0(4)2 + e0(24)
⇒ d2y/dx2 = 40.
Q.19. If  and its first derivative with respect to x is −(b/a)loge2 when x = 1, where a and b are integers, then the minimum value of |a2 − b2| is _______ (JEE Main 2021)
and its first derivative with respect to x is −(b/a)loge2 when x = 1, where a and b are integers, then the minimum value of |a2 − b2| is _______ (JEE Main 2021)
Ans. 481
= sin(2tan-12x)
⇒ a = 25, b = 12
|a2 − b2| = |625 − 144| = 481
|
347 docs|185 tests
|
|
347 docs|185 tests
|

|
Explore Courses for JEE exam
|

|



















































































