JEE Main Previous year questions (2021-22): Differentiation | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download

Q.1. Let 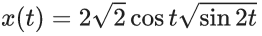 and  Then 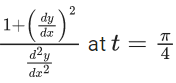 is equal to :     (JEE Main 2022)
(a)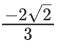
(b) 2/3
(c) 1/3
(d) (-2)/3

Ans. d

Q.2. The value of log_e⁡2(d/dx)(log_cos⁡x⁡cosecx) at x = π/4 is     (JEE Main 2022)
(a) -2/√2
(b) 2√2
(c) -4
(d) 4

Ans. d
Let f(x) = log_cos⁡xcos⁡ ec x


at x = π/4

∴ log_e2f′(x) at x = π/4 = 4

Q.3. If y = tan⁻¹(sec⁡x³ − tan⁡x³) ,π/2 < x³ < 3π/2, then      (JEE Main 2022)
(a) xy″ + 2y′ = 0
(b) x²y″ − 6y + (3π/2) = 0
(c) x²y″ − 6y + 3π = 0
(d) xy″−4y′ = 0

Ans. b

∴ y = tan^-1(secθ - tanθ)




y" = -3x

Q.4. If cos⁻¹(y/2) = log_e(x/5)⁵, |y| < 2, then :     (JEE Main 2022)
(a) x²y″ + xy′ − 25y = 0
(b) x²y″ − xy′ − 25y = 0
(c) x²y″ − xy′ + 25y = 0
(d) x²y″ + xy′ + 25y = 0

Ans. d

Differentiating on both side


Square on both side

Diff on both side
2xy′² + 2y′y″x² = −25 × 2yy′
xy' + y"x² + 25y = 0

Q.5. Let f : R → R be a function defined by f(x) = n₁, n₂ ∈ N. Then, which of the following is NOT true?     (JEE Main 2022)
(a) For n1 = 3, n2 = 4, there exists α ∈ (3, 5) where f attains local maxima.
(b) For n1 = 4, n2 = 3, there exists α ∈ (3, 5) where f attains local minima.
(c) For n1 = 3, n2 = 5, there exists α ∈ (3, 5) where f attains local maxima.
(d) For n1 = 4, n2 = 6, there exists α ∈ (3, 5) where f attains local maxima.

Ans. c
Given,
f(x) =
Differentiating both side with respect to x, we get


Option A :
When n₁ = 3 and n₂ = 4 then
f′(x) = (x−3)³⁻¹ (x−5)⁴⁻¹ [3(x−5) + 4(x−3)]
= (x − 3)²(x − 5)³(7x − 27)
Critical point is at x = 3, 5 and 27/7

When value of f'(x) is less than (27/5), f'(x) is positive means slope of f(x) graph is positive.
And when value of f'(x) is greater than (27/7) but less than 5 then f'(x) is negative means slope of f(x) is negative.

So at (27/7) between 3 and 5, f(x) attain local maxima.
∴ Option A is correct.
Option B :
When n₁ = 4 and n₂ = 3 then
f′(x) = (x−3)⁴⁻¹(x−5)³⁻¹[4(x−5) + 3(x−3)]
= (x−3)³(x−5)²(7x−29)
Critical point is at x = 3, 5 and 29/7

When f'(x) is less than 29/7 but greater than 3 then f'(x) is negative means slope of graph of f(x) is negative.
And when f'(x) is greater than 29/7 but less than 5 then f'(x) is positive means slope of graph of f(x) is positive.

So at 29/7 between 3 and 5, f(x) attain local minima.
∴ Option (B) is correct.
Option C :
When n₁ = 3 and n² = 5 then
f′(x) = (x−3)³⁻¹ (x−5)⁵⁻¹ [3(x−5) + 5(x−3)]
= (x−3)² (x−5)⁴ (8x−30)
Critical point is at x = 3, 5 and

When f'(x) is less than (30/8) but greater than 3 then f'(x) is negative means slope of graph of f(x) is negative.
And when f'(x) is greater than (30/8) but less than 5 then f'(x) is positive means slope of graph of f(x) is positive.

So, at (30/8) between 3 and 5, f(x) attain local minima.
∴ Option C is not true.
Similarly you can check option D also.

Q.6. Let 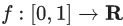 be a twice differentiable function in (0, 1) such that f(0) = 3 and f(1) = 5. If the line y = 2x + 3 intersects the graph of f at only two distinct points in (0, 1), then the least number of points x ∈ (0, 1), at which f′′(x) = 0, is _____.      (JEE Main 2022)

Ans. 2

If a graph cuts y = 2x + 5 in (0, 1) twice then its concavity changes twice.
∴ f′(x) = 0 at at least two points.

Q.7. Let  where [α] denotes the greatest integer less than or equal to α. Then the number of points 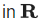 where f is not differentiable is ___________.    (JEE Main 2022)

Ans. 3




∴ Non-diff at x = 1/4,

Q.8. If y(x) = (x^x)^x, x > 0, then (d²x/dy²) + 20 at x = 1 is equal to _____.     (JEE Main 2022)

Ans. 16

Q.9. Let f and g be twice differentiable even functions on (−2, 2) such that f(1/4) = 0, f(1/2) = 0, f(1) = 1 and g(3/4) = 0, g(1) = 2. Then, the minimum number of solutions of f(x)g″(x) + f′(x)g′(x) = 0 in (−2,2) is equal to ________.     (JEE Main 2022)

Ans. 4

Q.10. The function f(x) = x³ − 6x² + ax + b is such that f(2) = f(4) = 0. Consider two statements:
Statement 1 : there exists x₁, x₂ ∈(2, 4), x₁ < x₂, such that f'(x₁) = −1 and f'(x₂) = 0.
Statement 2 : there exists x₃, x₄ ∈ (2, 4), x₃ < x₄, such that f is decreasing in (2, x₄), increasing in (x₄, 4) and 2f′(x₃) = √3f(x₄).
Then     (JEE Main 2021)
(a) both Statement 1 and Statement 2 are true
(b) Statement 1 is false and Statement 2 is true
(c) both Statement 1 and Statement 2 are false
(d) Statement 1 is true and Statement 2 is false

Ans. a
f(x) = x³ − 6x² + ax + b
f(2) = 8 − 24 + 2a + b = 0
2a + b = 16 .... (1)
f(4) = 64 − 96 + 4a + b = 0
4a + b = 32 .... (2)
Solving (1) and (2)
a = 8, b = 0
f(x) = x³ − 6x² + 8x
f′(x) = 3x² − 12x + 8
f″(x) = 6x− 12
⇒ f'(x) is ↑ for x > 2, and f'(x) is ↓ for x < 2
f′(2) = 12 − 24 + 8 = −4
f′(4) = 48 − 48 + 8 = 8
f′(x) = 3x² − 12x + 8
vertex (2, −4)
f'(2) = −4, f'(4) = 8, f'(3) = 27 − 36 + 8

f'(x₁) = −1, then x₁ = 3
f'(x₂) = 0
Again
f'(x) < 0 for x ∈ (2, x₄)
f'(x) > 0 for x ∈ (x₄, 4)
x₄ ∈ (3, 4)
f(x) = x³ − 6x² + 8x
f(3) = 27 − 54 + 24 = −3
f(4) = 64 − 96 + 32 = 0
For x₄(3, 4)
f(x₄) < −3√3
and f'(x₃) > −4
2f'(x₃) > −8
So, 2f'(x₃) = √3 f(x4)
Correct Ans. (a).

Q.11. If 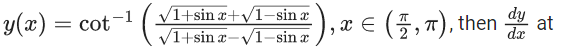 x = 5π/6 is:     (JEE Main 2021)
(a) -(1/2)
(b) -1
(c) 1/2
(d) 0

Ans. a


y'(x) = (-1)/2

Q.12. The local maximum value of the function 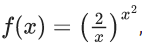 x > 0, is     (JEE Main 2021)
(a) (2√e)^1/e
(b) (4/√e)^e/4
(c) (e)^2/e
(d) 1

Ans. c







LM = 2/√e
Local maximum value =

Q.13. Let A=[a_ij] be a 3 × 3 matrix, where
Let a function f : R → R be defined as f(x) = det(A). Then the sum of maximum and minimum values of f on R is equal to:     (JEE Main 2021)
(a) -(20/27)
(b) 88/27
(c)20/27
(d) -(88/27)

Ans. d

|A| = 4x³ − 4x² − 4x = f(x)
f′(x) = 4(3x² − 2x − 1) = 0
⇒ x = 1; x = ((−1)/3)
∴ f(1) = −4; f(−(1/3)) = 20/27
Sum = -4 + (20/7) = -(88/27)

Q.14. If Rolle's theorem holds for the function f(x) = x³ − ax² + bx − 4,  x ∈ [1, 2] with f′(4/3) = 0, then ordered pair (a, b) is equal to :     (JEE Main 2021)
(a) (−5, −8)
(b) (5, −8)
(c) (−5, 8)
(d) (5, 8)

Ans. d
f(1) = f(2)
⇒ 1 − a + b − 4 = 8 − 4a + 2b − 4
3a − b = 7 ..... (1)
f′(x) = 3x² − 2ax + b
⇒ f′(4/3) = 0 ⇒ 3 × (16/9) − (8/3)a + b = 0
⇒ −8a + 3b = −16 ..... (2)
∴ a = 5, b = 8

Q.15. Let f be a twice differentiable function defined on R such that f(0) = 1, f'(0) = 2 and f'(x) ≠ 0 for all x ∈ R. If 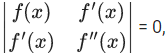 for all x ∈ R, then the value of f(1) lies in the interval :     (JEE Main 2021)
(a) (0, 3)
(b) (9, 12)
(c) (3, 6)
(d) (6, 9)

Ans. d

⇒ f(x).f″(x) − (f′(x))² = 0
Dividing by (f(x))², we get


Integrating both side,


⇒ 2/1 = c
⇒ c = 2

 

at x = 0,
ln|f(0)| = 0 + c′
⇒ 0 = 0 + c′
⇒ c′ = 0
∴ n|f(x)| = 2x
⇒ f(x) = e^2x
f(1) = e² = (2.71)² = 7.34
So it lie between (6, 9).

Q.16. Let f(x) be a cubic polynomial with f(1) = −10, f(−1) = 6, and has a local minima at x = 1, and f'(x) has a local minima at x = −1. Then f(3) is equal to ____.       (JEE Main 2021)

Ans. 22
Let f(x) = ax³ + bx² + cx + d
f'(x) = 3ax² + 2bx + c ⇒ f''(x) = 6ax + 2b
f'(x) has local minima at x = −1, so
∵ f''(−1) = 0 ⇒ −6a + 2b = 0 ⇒ b = 3a ..... (i)
f(x) has local minima at x = 1
f'(1) = 0
⇒ 3a + 6a + c = 0
⇒ c = −9a ..... (ii)
f(1) = −10
⇒ −5a + d = −10 ..... (iii)
f(−1) = 6
⇒ 11a + d = 6 ..... (iv)
Solving Eqs. (iii) and (iv)
a = 1, d = −5
From Eqs. (i) and (ii),
b = 3, c = −9
∴ f(x) = x³ + 3x² − 9x − 5
So, f(3) = 27 + 27 − 27 − 5 = 22

Q.17. If 'R' is the least value of 'a' such that the function f(x) = x² + ax + 1 is increasing on [1, 2] and 'S' is the greatest value of 'a' such that the function f(x) = x² + ax + 1 is decreasing on [1, 2], then the value of |R − S| is _____.       (JEE Main 2021)

Ans. 2
f(x) = x² + ax + 1
f'(x) = 2x + a
when f(x) is increasing on [1, 2]
2x + a ≥ 0 ∀ x ∈ [1, 2]
a ≥ −2x ∀ x ∈ [1, 2]
R = −4
when f(x) is decreasing on [1, 2]
2x + a ≤ 0 ∀ x ∈ [1, 2]
a ≤ −2 ∀ x ∈ [1, 2]
S = −2
|R − S| = | −4 + 2 | = 2

Q.18. If y = y(x) is an implicit function of x such that log_e(x + y) = 4xy, then 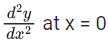 is equal to _____.       (JEE Main 2021)

Ans. 40
ln(x + y) = 4xy (At x = 0, y = 1)
x + y = e^4xy
⇒ 1 + (dy/dx) = e4xy(4x(dy/dx) + 4y)
At x = 0
dy/dx = 3

At x = 0, (d²y/dx²) = e⁰(4)² + e⁰(24)
⇒ d²y/dx² = 40.

Q.19. If  and its first derivative with respect to x is −(b/a)log_e2 when x = 1, where a and b are integers, then the minimum value of |a² − b²| is _______     (JEE Main 2021)

Ans. 481

= sin(2tan^-12^x)




⇒ a = 25, b = 12
|a² − b²| = |625 − 144| = 481