Karman-Pohlhausen Approximate Method For Solution Of Momentum Integral Equation Over A Flat Plate | Fluid Mechanics for Civil Engineering - Civil Engineering (CE) PDF Download
Karman-Pohlhausen Approximate Method For Solution Of Momentum Integral Equation Over A Flat Plate
- The basic equation for this method is obtained by integrating the x direction momentum equation (boundary layer momentum equation) with respect to y from the wall (at y = 0) to a distance δ(x) which is assumed to be outside the boundary layer. Using this notation, we can rewrite the Karman momentum integral equation as
(30.1)
- The effect of pressure gradient is described by the second term on the left hand side. For pressure gradient surfaces in external flow or for the developing sections in internal flow, this term contributes to the pressure gradient.
- We assume a velocity profile which is a polynomial of . η = y / δ, η being a form of similarity variable , implies that with the growth of boundary layer as distance x varies from the leading edge, the velocity profile u / U∞ remains geometrically similar.
- We choose a velocity profile in the form
(30.2)
In order to determine the constants a0,a1, a2, and a3 we shall prescribe the following boundary conditions
(30.3a)
(30.3b)
(30.3c)
(30.3d)
These requirements will yield respectively
Finally, we obtain the following values for the coefficients in Eq. (30.2),
and the velocity profile becomes
(30.4)
For flow over a flat plate, and the governing Eq. (30.1) reduces to
(30.5)
Again from Eq. (29.8), the momentum thickness is
The wall shear stress is given by
- Substituting the values of δ** and τw in Eq. (30.5) we get,
(30.6)
where C1 is any arbitrary unknown constant.
- The condition at the leading edge (at x = 0, δ = 0) yields C1 = 0
Finally we obtain,
(30.7)
(30.8)
- This is the value of boundary layer thickness on a flat plate. Although, the method is an approximate one, the result is found to be reasonably accurate. The value is slightly lower than the exact solution of laminar flow over a flat plate . As such, the accuracy depends on the order of the velocity profile. We could have have used a fourth order polynomial instead --
(30.9)
- In addition to the boundary conditions in Eq. (30.3), we shall require another boundary condition at
- This yields the constants as
. Finally the velocity profile will be
- Subsequently, for a fourth order profile the growth of boundary layer is given by
(30.10)
Integral Method For Non-Zero Pressure Gradient Flows
- A wide variety of "integral methods" in this category have been discussed by Rosenhead . The Thwaites method is found to be a very elegant method, which is an extension of the method due to Holstein and Bohlen . We shall discuss the Holstein-Bohlen method in this section.
- This is an approximate method for solving boundary layer equations for two-dimensional generalized flow. The integrated Eq. (29.14) for laminar flow with pressure gradient can be written as
or
(30.11)
- The velocity profile at the boundary layer is considered to be a fourth-order polynomial in terms of the dimensionless distance η = y / δ, and is expressed as
The boundary conditions are
- A dimensionless quantity, known as shape factor is introduced as
(30.12)
- The following relations are obtained
- Now, the velocity profile can be expressed as
(30.13)
where
- The shear stress
is given by
(30.14)
- We use the following dimensionless parameters,
(30.15)
(30.16)
(30.17)
- The integrated momentum Eq. (30.10) reduces to
(30.18)
- The parameter L is related to the skin friction
- The parameter K is linked to the pressure gradient.
- If we take K as the independent variable . L and H can be shown to be the functions of K since
(30.19)
(30.20)
(30.21)
Therefore,
- The right-hand side of Eq. (30.18) is thus a function of K alone. Walz pointed out that this function can be approximated with a good degree of accuracy by a linear function of K so that
- Equation (30.18) can now be written as
Solution of this differential equation for the dependent variable subject to the boundary condition U = 0 when x = 0 , gives
- With a = 0.47 and b = 6. the approximation is particularly close between the stagnation point and the point of maximum velocity.
- Finally the value of the dependent variable is
(30.22)
- By taking the limit of Eq. (30.22), according to L'Hopital's rule, it can be shown that
This corresponds to K = 0.0783.
- Note that
is not equal to zero at the stagnation point. If
is determined from Eq. (30.22),K(x) can be obtained from Eq. (30.16).
- Table 30.1 gives the necessary parameters for obtaining results, such as velocity profile and shear stress τw The approximate method can be applied successfully to a wide range of problems.
Table 30.1 Auxiliary functions after Holstein and Bohlen
- As mentioned earlier, K and
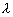 are related to the pressure gradient and the shape factor.
are related to the pressure gradient and the shape factor. - Introduction of K and
 in the integral analysis enables extension of Karman-Pohlhausen method for solving flows over curved geometry. However, the analysis is not valid for the geometries, where
in the integral analysis enables extension of Karman-Pohlhausen method for solving flows over curved geometry. However, the analysis is not valid for the geometries, where
Point of Seperation
For point of seperation
|
54 videos|141 docs|115 tests
|
FAQs on Karman-Pohlhausen Approximate Method For Solution Of Momentum Integral Equation Over A Flat Plate - Fluid Mechanics for Civil Engineering - Civil Engineering (CE)
| 1. What is the Karman-Pohlhausen approximate method? |  |
| 2. How does the Karman-Pohlhausen approximate method work? |  |
| 3. What is the significance of the momentum integral equation in civil engineering? |  |
| 4. What are the limitations of the Karman-Pohlhausen approximate method? |  |
| 5. How can the Karman-Pohlhausen approximate method be applied in practical civil engineering applications? |  |





















