Irodov Solutions: Kinematics - 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 16. Two particles, 1 and 2, move with constant velocities v1 and v2 along two mutually perpendicular straight lines toward the intersection point 0. At the moment t = 0 the particles were located at the distances l1 a nd l2 from the point 0. How soon will the distance between the particles become the smallest? What is it equal to?
Ans. Let the particle 1 and 2 be at points B and A at t = 0 at the distances l1 and l2 from intersection point O .
Let us fix the inertial frame with the particle 2. Now the particle 1 moves in relative to this reference frame with a relative velocity 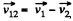 and its trajectory is the straight line BP. Obviously, the minimum distance between the particles is equal to the length of the perpendicular AP dropped from point A on to the straight line BP (Fig.).
and its trajectory is the straight line BP. Obviously, the minimum distance between the particles is equal to the length of the perpendicular AP dropped from point A on to the straight line BP (Fig.).
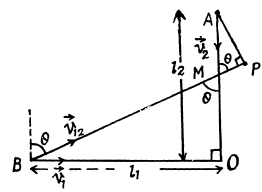
From Fig. (b), 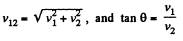 (1)
(1)
The shortest distaiice
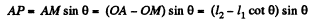
or 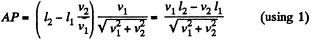
The sought time can be obtained directly from the condition that 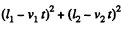 is minimum. This gives
is minimum. This gives 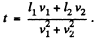
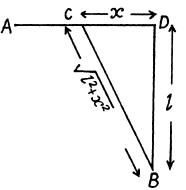
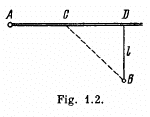
Q. 17. From point A located on a highway (Fig. 1.2) one has to get by car as soon as possible to point B located in the field at a distance 1 from the highway. It is known that the car moves in the field ri times slower than on the highway. At what distance from point D one must turn off the highway?
Ans. Let the car turn off the highway at a distance x from the point D.
So, CD = x, and if the speed of the car in the field is v, then the time taken by the car to cover the distance AC = AD - x on the highway
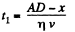 (1)
(1)
and the time taken to travel the distance CB in the field
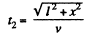 (2)
(2)
So, the total time elapsed to move the car from point A to B
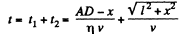
For t to be minimum
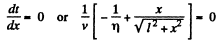
or 
Q. 18. A point travels along the x axis with a velocity whose projection vx is presented as a function of time by the plot in Fig. 1.3.
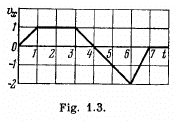
Assuming the coordinate of the point x = 0 at the moment t = 0, draw the approximate time dependence plots for the acceleration wx, the x coordinate, and the distance covered s.
Ans. To plot x (f), s (t) and wx (t) let us partion the given plot vx (t) into five segments (for detailed analysis) as shown in the figure.
For the part oa : wx =1 and vx = t = v
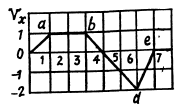
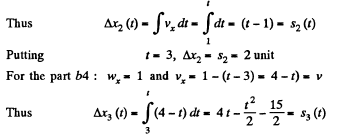
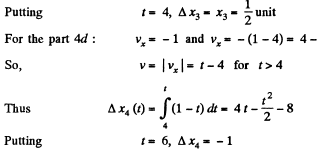
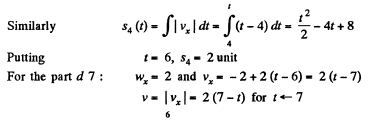
On the basis of these obtained expressions wx (r), x (;t) and s (t) plots can be easily plotted as shown in the figure of answersheet
Q. 19. A point traversed half a circle of radius R = 160 cm during time interval τ = 10.0 s. Calculate the following quantities averaged over that time:
(a) the mean velocity (v);
(b) the modulus of the mean velocity vector |(v)|;
(c) the modulus of the mean vector of the total acceleration |(w)|
if the point moved with constant tangent acceleration.
Ans. (a) Mean velocity

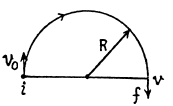
(b) Modulus of mean velocity vector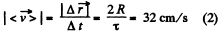
(c) Let the point moves from i to /along the half circle (Fig.) and v0 and v be the spe at the points respectively.
We have 
or, 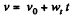 (as wt is constant, according to the problem)
(as wt is constant, according to the problem)
So, 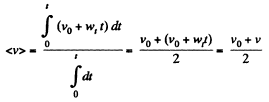
So, from (1) and (3) 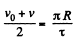
Now the modulus of the mean vector of total acceleration
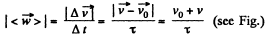
Using (4) in (5), we get : 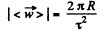
Q.20. A radius vector of a particle varies with time t as r = at (1 — αt), where a is a constant vector and α is a positive factor.
Find:
(a) the velocity v and the acceleration w of the particle as functions of time;
(b) the time interval Δt taken by the particle to return to the initial points, and the distance s covered during that time.
Ans. (a) we have 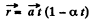
So 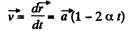
and 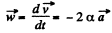
(b) From the equation
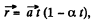
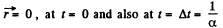
So, the sought time 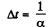
As 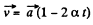
So 
Hence, the sought distance
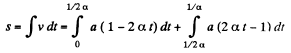
Simplifying, 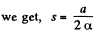
Q.21. At the moment t = 0 a particle leaves the origin and moves in the positive direction of the x axis. Its velocity varies with time as v = v0, (1 — t/τ), where v0 is the initial velocity vector whose modulus equals v0 = 10.0 cm/s; τ = 5.0 s.
Find:
(a) the x coordinate of the particle at the moments of time 6.0, 10, and 20 s;
(b) the moments of time when the particle is at the distance 10.0 cm from the origin;
(c) the distance s covered by the particle during the first 4.0 and 8.0 s; draw the approximate plot s (t).
Ans. (a) As the particle leaves the origin at t = 0
So, 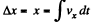 (1)
(1)
As 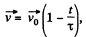
where 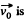 s directed towards the +ve x-axis
s directed towards the +ve x-axis
So, 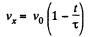 (2)
(2)
From (1) and (2),
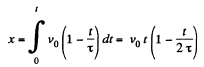 (3)
(3)
Hence x coordinate of the particle at t = 6 s.
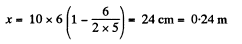
Similarly at
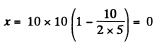
and at
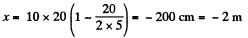
(b) At the moments the particle is at a distance of 10 cm from the origin, x = ± 10 cm.
Putting x = +10 in Eq. (3)
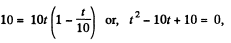
So, 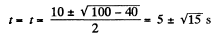
Now putting x = -10in Eqn (3)
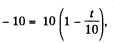
On solving, 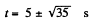
As t cannot be negative, so,
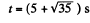
Hence the particle is at a distance of 10 cm from the origin at three moments of time :
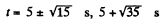
(c) We have 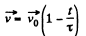
So, 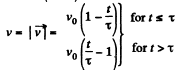
So 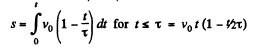
and
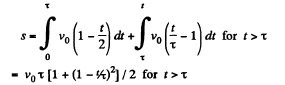 (A)
(A)
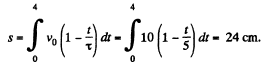
And for t = 8 s
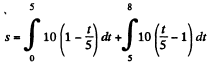
On integrating and simplifying, we get s = 34 cm.
On the basis of Eqs. (3) and (4), x (t) and s (t) plots can be drawn as shown in the answer sheet.
Q.22. The velocity of a particle moving in the positive direction of the x axis varies a 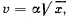 here α is a positive constant. Assuming that at the moment t = 0 the particle was located at the point x = 0, find:
here α is a positive constant. Assuming that at the moment t = 0 the particle was located at the point x = 0, find:
(a) the time dependence of the velocity and the acceleration of the particle;
(b) the mean velocity of the particle averaged over the time that the particle takes to cover the first s metres of the path.
Ans. As particle is in unidirectional motion it is directed along the jc-axis all the time. As at t = 0, x = 0
So, 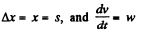
Therefore, 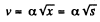
or, 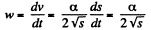
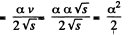 (1)
(1)
As, 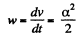
On integrating, 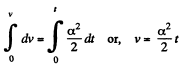 (2)
(2)
(b ) Lets be the time to cover first s m of the path. From the Eq.

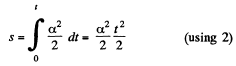
or 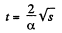 (3)
(3)
The mean velocity of particle
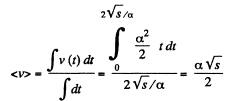
Q.23. A point moves rectilinearly with deceleration whose modulus depends on the velocity v of the particle as 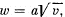 where a is a positive constant. At the initial moment the velocity of the point is equal to v0. 'What distance will it traverse before it stops? What time will it take to cover that distance?
where a is a positive constant. At the initial moment the velocity of the point is equal to v0. 'What distance will it traverse before it stops? What time will it take to cover that distance?
Ans. According to the problem
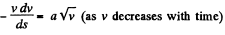
or, 
On integrating w e get 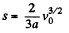
Again according to the problem
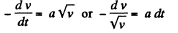
or, 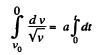
Thus 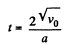
Q.24. A radius vector of a point A relative to the origin varies with time t as r = ati — bt2j, where a and b are positive constants, and i and j are the unit vectors of the x and y axes.
Find:
(a) the equation of the point's trajectory y (x); plot this function;
(b) the time dependence of the velocity v and acceleration w vectors, as well as of the moduli of these quantities;
(c) the time dependence of the angle α between the vectors w and v;
(d) the mean velocity vector averaged over the first t seconds of motion, and the modulus of this vector
Ans. (a) As 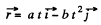
So, 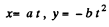
and therefore 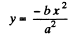
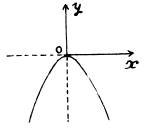
which is Eq. of a parabola, whose graph is shown in the Fig.
(b) As 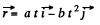
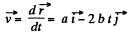 (1)
(1)
So, 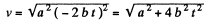
Diff. Eq. (1) w.r.t. time, we get
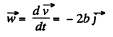
So, 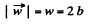
(c) 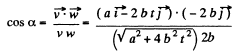
or, 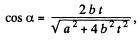
so, 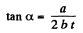
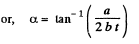
(d) The mean velocity vector
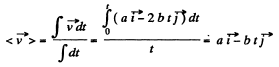
Hence, 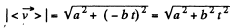
Q.25. A point moves in the plane xy according to the law x = at, y = at (1. — αt), where a and a are positive constants, and t is time.
Find:
(a) the equation of the point's trajectory y (x); plot this function;
(b) the velocity v and the acceleration w of the point as functions of time;
(c) the moment t0 at which the velocity vector forms an angle π/4 with the acceleration vector.
Ans. (a) We have
x = at and y = αt (1 - αt) (1)
Hence, y (x) becomes,
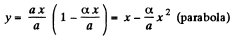
(b) Diiferentiating Eq. (1) we get
vx = a and vy = a (1 - 2αt) (2)
So, 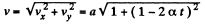
Diff. Eq. (2) with respect to time
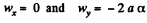
So, 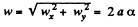
(c) From Eqs. (2) and (3)
We have
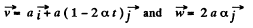
So, 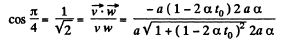
On simplifying. 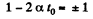
As, 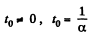
Q.26. A point moves in the plane xy according to the law x = a sin cot, y = a (1 — cos ωt), where a and co are positive constants.
Find:
(a) the distance s traversed by the point during the time T;
(b) the angle between the point's velocity and acceleration vectors.
Ans. Differentiating motion law : x = a sin ωt , y = a (1 - cos ωt ), with respect to time, vx = a ω cos ωt, vy = a ω sin ωt
So, 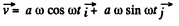 (1)
(1)
and 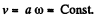 (2)
(2)
Differentiating Eq. (1) with respect to time
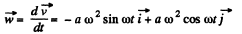 (3)
(3)
(a) The distance s traversed by the point during the time τ is given by
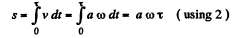
(b) Taking inner product of 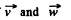
We get, 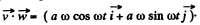
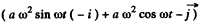
So, 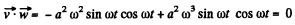
Thus, 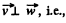 the angle between velocity vector and acceleration vector equals
the angle between velocity vector and acceleration vector equals 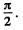
Q.27. A particle moves in the plane xy with constant acceleration w directed along the negative y axis. The equation of motion of the particle has the form y = ax — bx2, where a and b are positive constants. Find the velocity of the particle at the origin of coordinates.
Ans. Accordiing to the problem
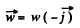
So, 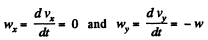 (1)
(1)
Differentiating Eq. of trajectory, y - ax - bx2, with respect to time
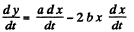 (2)
(2)
So,
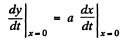
Again differentiating with respect to time
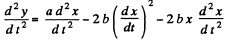
or, 
or, 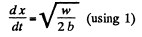
Using (3) in (2) 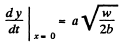
Hence, the velocity of the particle at the origin
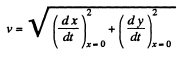

Hence, 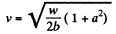
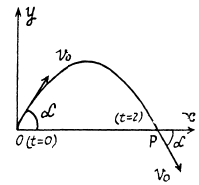
Q.28. A small body is thrown at an angle to the horizontal with the initial velocity v0. Neglecting the air drag,
find:
(a) the displacement of the body as a function of time r (t);
(b) the mean velocity vector (v) averaged over the first t seconds and over the total time of motion.
Ans. As the body is under gravity of constant accelration 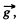 it’s ve lo c ity vector and displacemen vectors are:
it’s ve lo c ity vector and displacemen vectors are:
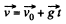 (1)
(1)
and 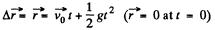 (2)
(2)
So, 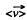 over the first t seconds
over the first t seconds
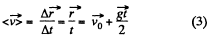
Hence from 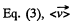 over the first t seconds
over the first t seconds
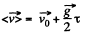 (4)
(4)
For evaluating ty take
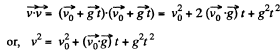
But we have v = v0 at t = 0 and
Also at t - x (Fig.) (also from energy conservation)
Hence using this propety in Eq. (5)
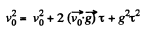
As 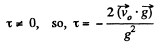
Putting this value of τ in Eq. (4), the average velocity over the time of flight
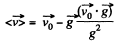
Q.29. A body is thrown from the surface of the Earth at an angle α to the horizontal with the initial velocity v0. Assuming the air drag to be negligible, find:
(a) the time of motion;
(b) the maximum height of ascent and the horizontal range; at what value of the angle α they will be equal to each other;
(c) the equation of trajectory y (x), where y and x are displacements of the body along the vertical and the horizontal respectively;
(d) the curvature radii of trajectory at its initial point and at its peak.
Ans. The body thrown in air with velocity v0 at an angle a from the horizontal lands at point P on the Earth's surface at same horizontal level (Fig.). The point of projection is taken as origin, so, Δx = x and Δy = y
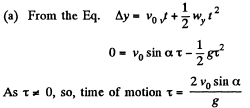
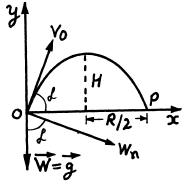
(b) At the maximum height of ascent, vy = 0
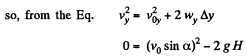
Hence maximum height 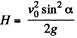
During the time of motion the net horizontal displacement or horizontal range, will be obtained by the equation
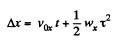
or, 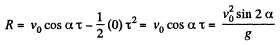
when R = H
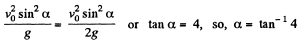
(c) For the body, x (t) and y (t) are
x = v0 cos α t (1)
and 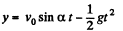 (2)
(2)
Hence putting the value of t from (1) into (2) we get,
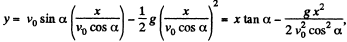
Which is the sought equation of trajectory i.e. y (x)
(d) As the body thrown in air follows a curve, it has some normal acceleration at all the moments of time during it’s motion in air.
At the initial point (x = 0, y = 0), from the equation :
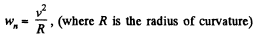
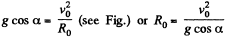
At the peak point 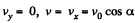 and the angential acceleration is zero.
and the angential acceleration is zero.
Now from the Eq. 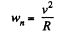
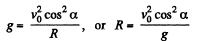
Note : We may use the formula of curvature radius of a trajectory y (x), to solve part (d)y
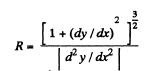
Q. 30. Using the conditions of the foregoing problem, draw the approximate time dependence of moduli of the normal wn and tangent wτ, acceleration vectors, as well as of the projection of the total acceleration vector wv on the velocity vector direction.
Ans. We have, vx = v0 cos α, vy = v0 sin α - gt
As 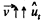 all the moments of time.
all the moments of time.
Thus 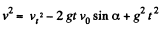
Now, 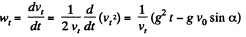
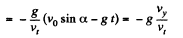
Hence 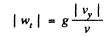
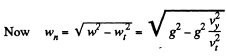
or 
As 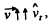 during time o f motion
during time o f motion
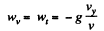
On the basis of obtained expressions or facts the sought plots can be drawn as shown in the figure of answer sheet



















