Kinetic Energy and the Law of Conservation of Energy | Science Class 9 PDF Download
Kinetic Energy
A moving object is capable of doing work because of it" motion. Hence, we say that the object has kinetic energy. "Kinetikos" in Greek means "to move". Hence,kinetic energy means energy due to motion. The energy is stored in the object when work is done to change its velocity from a lower value to a higher value, or from rest to certain velocity.
Kinetic energy of an object is defined as the energy which it possesses by virtue of its motion, and is measured by the amount of work that the object can do against an opposing force before it comes to rest.
Kinetic energy of an object moving with a certain velocity is equal to the work done on it to enable it to acquire that velocity.
Examples of bodies possessing Kinetic Energy
1. A ball rolling on a surface because it can set another ball into motion by striking it.
2. A bullet fired from a gun as it is able to penetrate some distance into a target which it strikes.
3. A tarpedo in motion as it can do work by penetrating into the side' of a ship.
4. Water in motion as it can turn a wheel or a turbine.
5. A fast wind as it can set a boat in motion when striking against its sail.
6. A moving hammer as it drives a nail into a wall against the resistance offered to it by the wall.
7. A falling body as it can break something on which it falls.
Expression for Kinetic Energy
Consider an object of mass m which is moving with an initial velocity u on a perfectly frictionless surface. Let a constant external force F act on it and produce an acceleration a in it. If v is the final velocity of the object after having undergone a displacements, then from
Work done by the force in displacing the body through s, i.e.,
W= F × s ..........(2)
We know from Newton's Second Law of Motion,
F = ma ...........(3)
From equation (1), (2) and (3), we get
If the object is initially at rest, u = 0 and as such from eqn. (4),
W = (1/2)mv2 ...........(5)
This work done (W) in making the object acquire a velocity v after starting from rest has not gone waste and is, in fact, stored in the object.
Work stored up in a moving object is called the kinetic energy of the object.
If kinetic energy of an object is denoted by Ek then
Ek =(1/2})mv2 ..............(6)
Kinetic energy of a moving object is defined as half the product of the mass of the object and the square of the speed of the object.
Work-Energy Theorem
The work-energy theorem states that the net work done by a moving body can be calculated by finding the change in KE.
⇒ W net = KE final − KE initial
⇒ Wnet= 1/2 x m[v2−u2]
Factors affecting Kinetic Energy
- Mass
- Velocity
- Momentum
Potential Energy
The energy possessed by an object by virtue of its position or configuration is called its potential energy. It is measured by the work that the object can do in passing from its present position or configuration to some standard position or configuration (known as zero position or zero-configuration).
The kinetic energy of mass m converts into elastic potential energy of spring.
Example:
Let a small mass m be released from a smooth inclined plane. Another mass M is kept at a rough horizontal plane at rest. The mass m will move along the inclined plane and strike the mass M. Both the masses will move along the horizontal surface for some distance and come to rest. The mass M moves a distance s by the force applied by m. Thus, m does work for which it requires energy. This energy is possessed by m at A as it was at a height h from the horizontal surface. This energy due to position is called potential energy. Precisely speaking this energy is called gravitational potential energy.
Thus potential energy is defined as follows:
The energy possessed by a body due to its position or change in shape is called potential energy.
Note: The energy possessed by a body due to its height from the surface of earth is called gravitational potential energy and that due to change in shape is called elastic potential energy.
Other examples where elastic potential energy is stored are:
(i) a stretched bow
(ii) a stretched rubber band
(iii) a wound spring
All above examples are because of change in shape.
Potential Energy of an Object at a Height
Let us consider a block of mass m kept on the surface of earth. Let the block be lifted to a height h. For that a force F is required which is equal to mg.
This force lifts the block through a distance h. The work done by this force,
∴ W = mg × h [ ∵ F = mg]W = F × h
This work is converted into potential energy (P.E.) of the block.
P.E = mgh
The expression shows that potential energy depends on
(a) mass m
(b) height h from ground
(c) acceleration due to gravity g
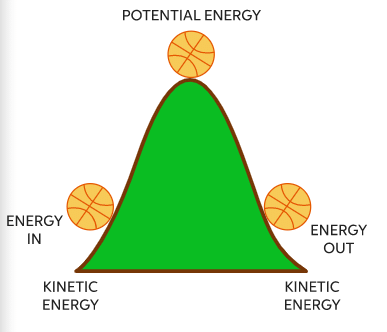
Law of Conservation of Energy
According to law of conservation of energy, energy can neither be created nor destroyed, it can be converted from one form to another.
Conservation of Mechanical Energy
Case: A ball is dropped from some height.
At point A: Let a ball of mass m is dropped from a height h. Here the total energy (T.E.) of the ball is the sum of kinetic energy (K.E.) and potential energy (P.E.).
Potential energy = mgh
Kinetic energy = 1/2 m (0)2 = 0 (u = 0)
∴ [T.E.]A = mgh 0 = mgh ... (A)
At point B: Let the ball travel a distance of h1 in time t during its fall. Then the velocity of the ball after time t can be found by using equation of motion. u = 0, a = g, S = h1, v = v
Using v2 - u2 = 2as
v2 - u2 = 2gh1
⇒ v2 = 2gh1
Now K.E. at B = 1/2 mv2 = 1/2m × 2gh1 = mgh1
P.E. at B = mg (h - h1)
Total energy at B = K.E. + P.E. = mgh1 + mg(h - h1) = mgh ... (B)
At point C: Suppose the ball cover a distance h when it moves from A to C. Let V be the velocity of the ball at point C just before it thouches the ground, then
v2 - u2 = 2gh
v2 - 0 = 2gh or v2 = 2gh therefore
Kinetic energy (K.E.) = 1/2 mv2 = 1/2 m (2gh) = mgh
and potential energy at C ∴ P.E. = 0
Hence total energy at point C.
E = K.E. + P.E. = mgh 0 = mgh ... (C)
Thus it is clear from equations A, B and C, that the total mechanical energy of a freely falling ball remain constant. There is, simply, a transformation of mechanical energy. This transformation is depicted in the graph of figure.
|
84 videos|478 docs|60 tests
|
FAQs on Kinetic Energy and the Law of Conservation of Energy - Science Class 9
| 1. What is potential energy? |  |
| 2. How is potential energy related to an object's height? |  |
| 3. What is the law of conservation of energy? |  |
| 4. How is kinetic energy related to the law of conservation of energy? |  |
| 5. What are some examples of potential energy? |  |






















