Kirchhoff’s Current Law | Network Theory (Electric Circuits) - Electrical Engineering (EE) PDF Download
Introduction
- Gustav Kirchhoff’s Current Law is one of the fundamental laws used for circuit analysis. His current law states that for a parallel path the total current entering a circuits junction is exactly equal to the total current leaving the same junction. This is because it has no other place to go as no charge is lost.
- In other words the algebraic sum of ALL the currents entering and leaving a junction must be equal to zero as: Σ IIN = Σ IOUT.
- This idea by Kirchhoff is commonly known as the Conservation of Charge, as the current is conserved around the junction with no loss of current. Lets look at a simple example of Kirchhoff’s current law (KCL) when applied to a single junction.
A Single Junction
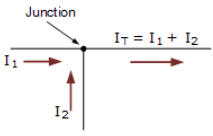
- Here in this simple single junction example, the current IT leaving the junction is the algebraic sum of the two currents, I1 and I2 entering the same junction. That is IT = I1 + I2.
Note that we could also write this correctly as the algebraic sum of: IT – (I1 + I2) = 0.
So if I1 equals 3 amperes and I2 is equal to 2 amperes, then the total current, IT leaving the junction will be 3 + 2 = 5 amperes, and we can use this basic law for any number of junctions or nodes as the sum of the currents both entering and leaving will be the same. - Also, if we reversed the directions of the currents, the resulting equations would still hold true for I1 or I2. As I1 = IT – I2 = 5 – 2 = 3 amps, and I2 = IT – I1 = 5 – 3 = 2 amps. Thus we can think of the currents entering the junction as being positive (+), while the ones leaving the junction as being negative (-).
- Then we can see that the mathematical sum of the currents either entering or leaving the junction and in whatever direction will always be equal to zero, and this forms the basis of Kirchhoff’s Junction Rule, more commonly known as Kirchhoff’s Current Law, or (KCL).
Resistors in Parallel
- Let’s look how we could apply Kirchhoff’s current law to resistors in parallel, whether the resistances in those branches are equal or unequal. Consider the following circuit diagram:
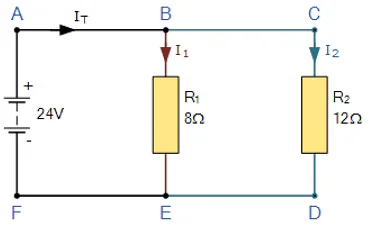
- In this simple parallel resistor example there are two distinct junctions for current. Junction one occurs at node B, and junction two occurs at node E. Thus we can use Kirchhoff’s Junction Rule for the electrical currents at both of these two distinct junctions, for those currents entering the junction and for those currents flowing leaving the junction.
- To start, all the current, IT leaves the 24 volt supply and arrives at point A and from there it enters node B. Node B is a junction as the current can now split into two distinct directions, with some of the current flowing downwards and through resistor R1 with the remainder continuing on through resistor R2 via node C. Note that the currents flowing into and out of a node point are commonly called branch currents.
- We can use Ohm’s Law to determine the individual branch currents through each resistor as: I = V/R, thus:
For current branch B to E through resistor R1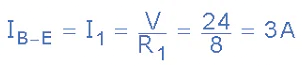
For current branch C to D through resistor R2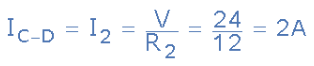
- From above we know that Kirchhoff’s current law states that the sum of the currents entering a junction must equal the sum of the currents leaving the junction, and in our simple example above, there is one current, IT going into the junction at node B and two currents leaving the junction, I1 and I2.
- Since we now know from calculation that the currents leaving the junction at node B is I1 equals 3 amps and I2 equals 2 amps, the sum of the currents entering the junction at node B must equal 3 + 2 = 5 amps. Thus ΣIN = IT = 5 amperes.
- In our example, we have two distinct junctions at node B and node E, thus we can confirm this value for IT as the two currents recombine again at node E. So, for Kirchhoff’s junction rule to hold true, the sum of the currents into point F must equal the sum of the currents flowing out of the junction at node E.
- As the two currents entering junction E are 3 amps and 2 amps respectively, the sum of the currents entering point F is therefore: 3 + 2 = 5 amperes. Thus ΣIN = IT = 5 amperes and therefore Kirchhoff’s current law holds true as this is the same value as the current leaving point A.
Applying KCL to more complex circuits.
- We can use Kirchhoff’s current law to find the currents flowing around more complex circuits. We hopefully know by now that the algebraic sum of all the currents at a node (junction point) is equal to zero and with this idea in mind, it is a simple case of determining the currents entering a node and those leaving the node. Consider the circuit below.
Kirchhoff’s Current Law Example
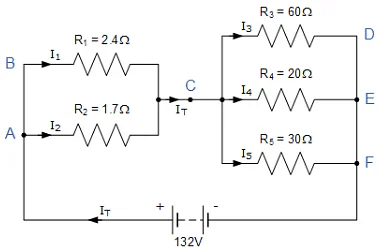
- In this example there are four distinct junctions for current to either separate or merge together at nodes A, C, E and node F. The supply current IT separates at node A flowing through resistors R1 and R2, recombining at node C before separating again through resistors R3, R4 and R5 and finally recombining once again at node F.
- But before we can calculate the individual currents flowing through each resistor branch, we must first calculate the circuits total current, IT. Ohms law tells us that I = V/R and as we know the value of V, 132 volts, we need to calculate the circuit resistances as follows.
Circuit Resistance RAC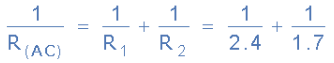

- Thus the equivalent circuit resistance between nodes A and C is calculated as 1 Ohm.
Circuit Resistance RCF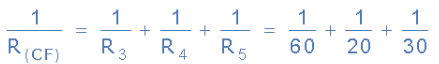

Thus the equivalent circuit resistance between nodes C and F is calculated as 10 Ohms. Then the total circuit current, IT is given as:
RT = R(AC) + R(CF) = 1 + 10 = 11Ω
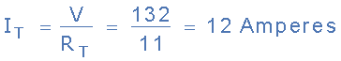
Giving us an equivalent circuit of: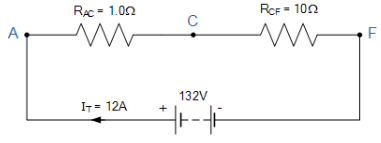
Therefore, V = 132V, RAC = 1Ω, RCF = 10Ω’s and IT = 12A.
Having established the equivalent parallel resistances and supply current, we can now calculate the individual branch currents and confirm using Kirchhoff’s junction rule as follows.
VAC = IT X RAC = 12 x 1 = 12 Volts
VCF = IT x RCF = 12 x 10 = 120 Volts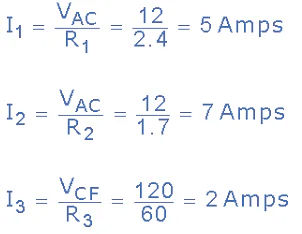
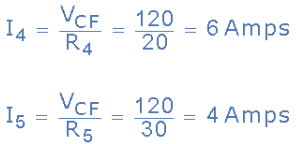
Thus, I1 = 5A, I2 = 7A, I3 = 2A, I4 = 6A, and I5 = 4A.
We can confirm that Kirchoff’s current law holds true around the circuit by using node C as our reference point to calculate the currents entering and leaving the junction as:
At node C ∑IIN = ∑IOUT
IT = I1 + I2 = I3 + I4 + I5
∴ 12 = (5 + 7) = (2 + 6 + 4)
We can also double check to see if Kirchhoff's Current Law holds true as the currents entering the junction are positive, while the ones leaving the junction are negative, thus the algebraic sum is: I1 + I2 – I3 – I4 – I5 = 0 which equals 5 + 7 – 2 – 6 – 4 = 0. So we can confirm by analysis that Kirchhoff’s current law (KCL) which states that the algebraic sum of the currents at a junction point in a circuit network is always zero is true and correct in this example.
Kirchhoff’s Current Law Example
Find the currents flowing around the following circuit using Kirchhoff’s Current Law only.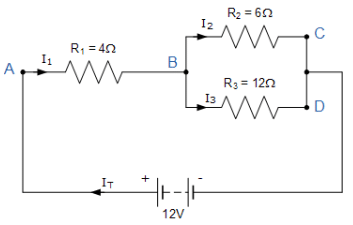
IT is the total current flowing around the circuit driven by the 12V supply voltage. At point A, I1 is equal to IT, thus there will be an I1*R voltage drop across resistor R1.
The circuit has 2 branches, 3 nodes (B, C and D) and 2 independent loops, thus the I*R voltage drops around the two loops will be:
Loop ABC ⇒ 12 = 4I1 + 6I2
Loop ABD ⇒ 12 = 4I1 + 12I3
Since Kirchhoff’s current law states that at node B, I1 = I2 + I3, we can therefore substitute current I1 for (I2 + I3) in both of the following loop equations and then simplify.
Kirchhoff’s Loop Equations
We now have two simultaneous equations that relate to the currents flowing around the circuit.
Eq. No 1 : 12 = 10I2 + 4I3
Eq. No 2 : 12 = 4I2 + 16I3
By multiplying the first equation (Loop ABC) by 4 and subtracting Loop ABD from Loop ABC, we can be reduced both equations to give us the values of I2 and I3
Eq. No 1 : 12 = 10I2 + 4I3 ( x4 ) ⇒ 48 = 40I2 + 16I3
Eq. No 2 : 12 = 4I2 + 16I3 ( x1 ) ⇒ 12 = 4I2 + 16I3
Eq. No 1 – Eq. No 2 ⇒ 36 = 36I2 + 0
Substitution of I2 in terms of I3 gives us the value of I2 as 1.0 Amps
Now we can do the same procedure to find the value of I3 by multiplying the first equation (Loop ABC) by 4 and the second equation (Loop ABD) by 10. Again by subtracting Loop ABC from Loop ABD, we can be reduced both equations to give us the values of I2 and I3
Eq. No 1 : 12 = 10I2 + 4I3 (x4) ⇒ 48 = 40I2 + 16I3
Eq. No 2 : 12 = 4I2 + 16I3 (x10) ⇒ 120 = 40I2 + 160I3
Eq. No 2 – Eq. No 1 ⇒ 72 = 0 + 144I3
Thus substitution of I3 in terms of I2 gives us the value of I3 as 0.5 Amps
As Kirchhoff’s junction rule states that : I1 = I2 + I3
The supply current flowing through resistor R1 is given as : 1.0 + 0.5 = 1.5 Amps
Thus I1 = IT = 1.5 Amps, I2 = 1.0 Amps and I3 = 0.5 Amps and from that information we could calculate the I*R voltage drops across the devices and at the various points (nodes) around the circuit.
|
73 videos|139 docs|62 tests
|
FAQs on Kirchhoff’s Current Law - Network Theory (Electric Circuits) - Electrical Engineering (EE)
| 1. What is Kirchhoff's current law? |  |
| 2. How can Kirchhoff's current law be applied in practical circuits? |  |
| 3. Can Kirchhoff's current law be violated? |  |
| 4. How is Kirchhoff's current law related to Kirchhoff's voltage law? |  |
| 5. Can Kirchhoff's current law be applied to both DC and AC circuits? |  |
















