Kirchhoff’s Laws of Electric Circuits | Additional Documents & Tests for IIT JAM PDF Download

Two simple relationships can be used to determine the value of currents in circuits. They are useful even in rather complex situations such as circuits with multiple loops. The first relationship deals with currents at a junction of conductors. Figure shows three such junctions, with the currents assumed to flow in the directions indicated.

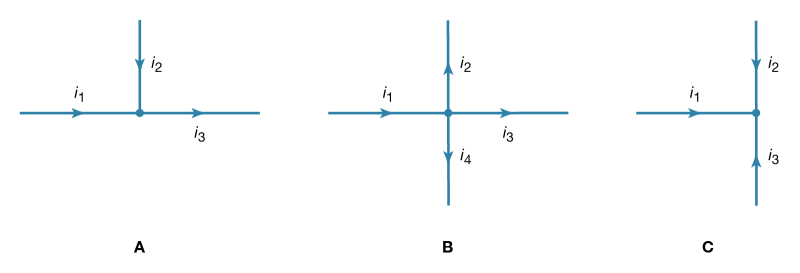
Figure: Electric currents at a junction (see text).

Simply stated, the sum of currents entering a junction equals the sum of currents leaving that junction. This statement is commonly called Kirchhoff’s first law (after the German physicist Gustav Robert Kirchhoff, who formulated it). For Figure, the sum is i₁ + i₂ = i₃. For Figure, i₁ = i₂ + i₃ + i₄. For Figure, i₁ + i₂ + i₃ = 0. If this last equation seems puzzling because all the currents appear to flow in and none flows out, it is because of the choice of directions for the individual currents. In solving a problem, the direction chosen for the currents is arbitrary. Once the problem has been solved, some currents have a positive value, and the direction arbitrarily chosen is the one of the actual current. In the solution some currents may have a negative value, in which case the actual current flows in a direction opposite that of the arbitrary initial choice.
Kirchhoff’s second law is as follows: the sum of electromotive forces in a loop equals the sum of potential drops in the loop. When electromotive forces in a circuit are symbolized as circuit components as in Figure, this law can be stated quite simply: the sum of the potential differences across all the components in a closed loop equals zero. To illustrate and clarify this relation, one can consider a single circuit with two sources of electromotive forces E₁ and E₂, and two resistances R₁ and R₂, as shown in Figure. The direction chosen for the current i also is indicated. The letters a, b, c, and d are used to indicate certain locations around the circuit. Applying Kirchhoff’s second law to the circuit,

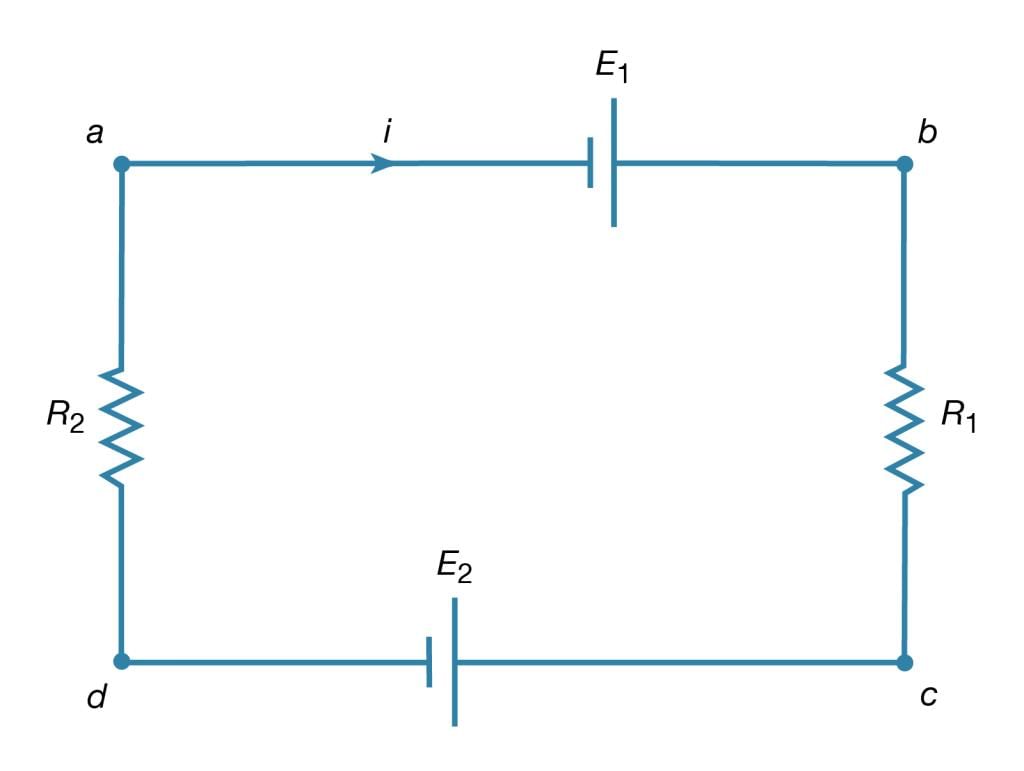
Figure: Circuit illustrating Kirchhoff's loop equation (see text). 

 (26)

Referring to the circuit in Figure, the potential differences maintained by the electromotive forces indicated are V_b − V_a = E₁, and V_c − V_d = −E₂. From Ohm’s law, V_b − V_c = iR₁, and V_d − V_a = iR₂. Using these four relationships in equation (26), the so-called loop equation becomes E₁ − E₂− iR₁ − iR₂ = 0.
Given the values of the resistances R₁ and R₂ in ohms and of the electromotive forces E₁ and E₂in volts, the value of the current i in the circuit is obtained. If E₂ in the circuit had a greater value than E₁, the solution for the current i would be a negative value for i. This negative sign indicates that the current in the circuit would flow in a direction opposite the one indicated in Figure.
Kirchhoff’s laws can be applied to circuits with several connected loops. The same rules apply, though the algebra required becomes rather tedious as the circuits increase in complexity.