The funds they received, in descending order, were Rs.390,000, Rs.210,000, Rs.165,000, Rs.77,000, and Rs.66,000. ∴ The product of tokes = 390, 210, 165, 77, 66 ⇒ Break of tokens received From (1): Fathima awarded tokens to everyone except Qahira, From (1): Adhara awarded tokens to no one except Pragnyaa From (2): Rashida received the highest number of tokens that anyone received, but she did not receive one from Esther. From (3): Dhanavi awarded a token to Qahira but not to Smera. From (3): Bithi awarded a token to Smera but not to Qahira If Bithi gives token number 2 to S/T, then Chhaya will given token number 5 to T/S and vice-a-versa. ∴ Qahira received two tokens i.e., 7 and 11.
390 = 2 × 3 × 5 × 13
210 = 2 × 3 × 5 × 7
165 = 3 × 5 × 11
77 = 7 × 11
66 = 2 × 3 × 11
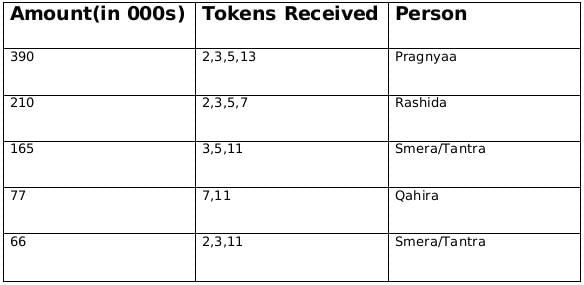
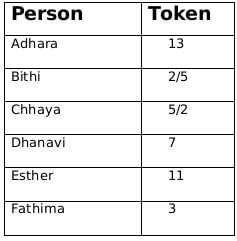
∴ Fatima must have awarded token number 3 to everyone and Qahira received tokens whose product is 77.
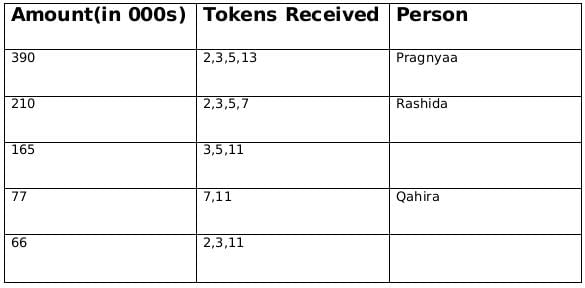
∴ Adhara must have awared token 13 and Pragnyaa received tokens whose product is 390.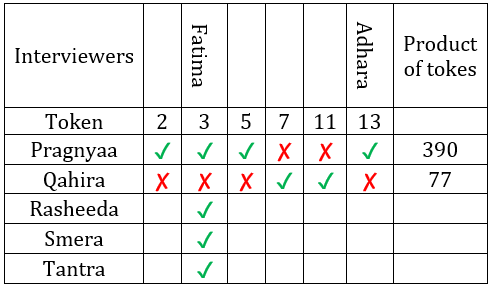
∴ Rashida must have received 4 tokes whose product can only be 210. Also, since Esther did not give her the token, hence Esther must have distributed token number 11.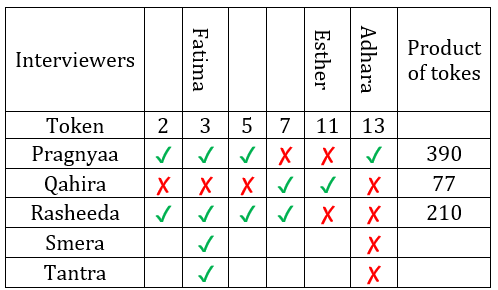
∴ Dhanavi must have awared token number 7.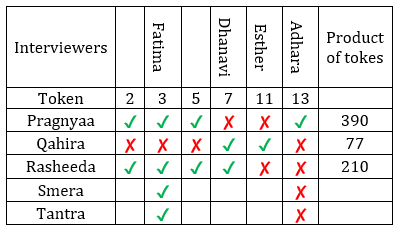
∴ Bithi/Chhaya could have awared token 2/5 in any order.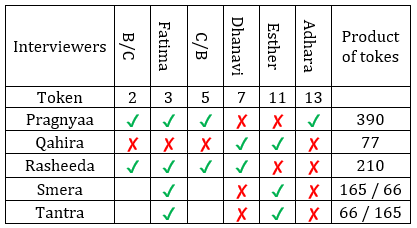
From statement 1 we can deduce that Fatima gave token 3 and Adhara gave token 13 and therefore from this we can say that Qahira received a funding of 77,000 and Pragnyaa received a funding of 390,000. From statement 2, we know that Rashida received highest number of tokens and we already concluded that Pragnyaa received a funding of 390,000 so we can say that Rashida received a funding of 210,000. Rashida did not received a token from Esther so we can also conclude that Esther gave the token number 11. From statement 3 we can conclude that Dhanavi gave a token of 7, and Bethi Gave a token of either 2 or 5 and similarly Chhaya also gave a token of 2 or 5. From, statement 1 we know that Fatima gave token to 4 people except Qahira so the token number given by Fatima is 3, and Adhara gave token only to Pragnyaa so the token number given by Adhara is 13. Therefore we can also say that Pragnyaa received 390,000 and Qahira received 77,000. From statement 2, we know that Rashida received highest number of tokens and we already concluded that Pragnyaa received a funding of 390,000 so we can say that Rashida received a funding of 210,000. Rashida did not received a token from Esther so we can also conclude that Esther gave the token number 11.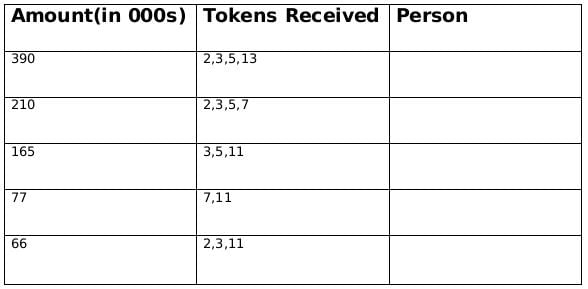
Alternate Explanation:
390=2×3×5×13
210=2×3×5×7
165=3×5×11
77=7×11
66=2×3×11
From the above information we can conclude that the number of times a particular token was given, therefore we get the following table,
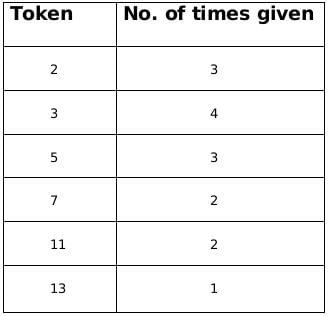
We know that there are five people who received the token and there are 6 people who awarded the token.
From statement 3, we can conclude that Dhanavi gave a token of 7, and Bethi Gave a token of either 2 or 5 and similarly Chhaya also gave a token of 2 or 5.
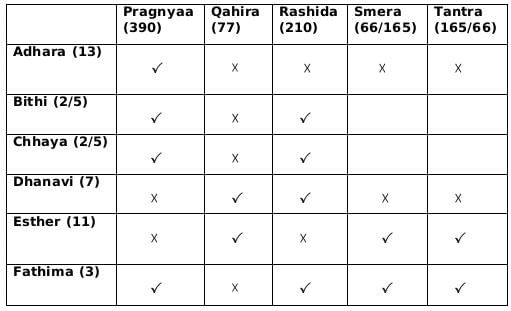
From statement 1 we can deduce that Fatima gave token 3 and Adhara gave token 13 and therefore from this we can say that Qahira received a funding of 77,000 and Pragnyaa received a funding of 390,000. From statement 2, we know that Rashida received highest number of tokens and we already concluded that Pragnyaa received a funding of 390,000 so we can say that Rashida received a funding of 210,000. Rashida did not received a token from Esther so we can also conclude that Esther gave the token number 11. From statement 3 we can conclude that Dhanavi gave a token of 7, and Bethi Gave a token of either 2 or 5 and similarly Chhaya also gave a token of 2 or 5. From, statement 1 we know that Fatima gave token to 4 people except Qahira so the token number given by Fatima is 3, and Adhara gave token only to Pragnyaa so the token number given by Adhara is 13. Therefore we can also say that Pragnyaa received 390,000 and Qahira received 77,000. From statement 2, we know that Rashida received highest number of tokens and we already concluded that Pragnyaa received a funding of 390,000 so we can say that Rashida received a funding of 210,000. Rashida did not received a token from Esther so we can also conclude that Esther gave the token number 11.



Alternate Explanation:
390=2×3×5×13
210=2×3×5×7
165=3×5×11
77=7×11
66=2×3×11
From the above information we can conclude that the number of times a particular token was given, therefore we get the following table,

We know that there are five people who received the token and there are 6 people who awarded the token.

From statement 3, we can conclude that Dhanavi gave a token of 7, and Bethi Gave a token of either 2 or 5 and similarly Chhaya also gave a token of 2 or 5.

From statement 1 we can deduce that Fatima gave token 3 and Adhara gave token 13 and therefore from this we can say that Qahira received a funding of 77,000 and Pragnyaa received a funding of 390,000. From statement 2, we know that Rashida received highest number of tokens and we already concluded that Pragnyaa received a funding of 390,000 so we can say that Rashida received a funding of 210,000. Rashida did not received a token from Esther so we can also conclude that Esther gave the token number 11. From statement 3 we can conclude that Dhanavi gave a token of 7, and Bethi Gave a token of either 2 or 5 and similarly Chhaya also gave a token of 2 or 5. From, statement 1 we know that Fatima gave token to 4 people except Qahira so the token number given by Fatima is 3, and Adhara gave token only to Pragnyaa so the token number given by Adhara is 13. Therefore we can also say that Pragnyaa received 390,000 and Qahira received 77,000. From statement 2, we know that Rashida received highest number of tokens and we already concluded that Pragnyaa received a funding of 390,000 so we can say that Rashida received a funding of 210,000. Rashida did not received a token from Esther so we can also conclude that Esther gave the token number 11.



Alternate Explanation:
390=2×3×5×13
210=2×3×5×7
165=3×5×11
77=7×11
66=2×3×11
From the above information we can conclude that the number of times a particular token was given, therefore we get the following table,

We know that there are five people who received the token and there are 6 people who awarded the token.

From statement 3, we can conclude that Dhanavi gave a token of 7, and Bethi Gave a token of either 2 or 5 and similarly Chhaya also gave a token of 2 or 5.

From statement 1 we can deduce that Fatima gave token 3 and Adhara gave token 13 and therefore from this we can say that Qahira received a funding of 77,000 and Pragnyaa received a funding of 390,000. From statement 2, we know that Rashida received highest number of tokens and we already concluded that Pragnyaa received a funding of 390,000 so we can say that Rashida received a funding of 210,000. Rashida did not received a token from Esther so we can also conclude that Esther gave the token number 11. From statement 3 we can conclude that Dhanavi gave a token of 7, and Bethi Gave a token of either 2 or 5 and similarly Chhaya also gave a token of 2 or 5. From, statement 1 we know that Fatima gave token to 4 people except Qahira so the token number given by Fatima is 3, and Adhara gave token only to Pragnyaa so the token number given by Adhara is 13. Therefore we can also say that Pragnyaa received 390,000 and Qahira received 77,000. From statement 2, we know that Rashida received highest number of tokens and we already concluded that Pragnyaa received a funding of 390,000 so we can say that Rashida received a funding of 210,000. Rashida did not received a token from Esther so we can also conclude that Esther gave the token number 11.
(a) Rs. 66,000
(b) Rs. 165,000




Alternate Explanation:
390=2×3×5×13
210=2×3×5×7
165=3×5×11
77=7×11
66=2×3×11
From the above information we can conclude that the number of times a particular token was given, therefore we get the following table,

We know that there are five people who received the token and there are 6 people who awarded the token.

From statement 3, we can conclude that Dhanavi gave a token of 7, and Bethi Gave a token of either 2 or 5 and similarly Chhaya also gave a token of 2 or 5.

In the east-west direction, a train starts from station M every 10 minutes.
Now the first train leaving station M is at 6:00 am.
Since every 10 minutes trains are available in east-west direction, the train timings leaving from M will be like 6:10 am, 6:20 am, 6:30 am and so on.
Given, Hari has reached station M by 8:05 am.
So the earliest by which Hari can catch a train from station M is 8:10 am.
Now there are 19 stations between M and n, out of which two stations are junctions.
Time taken to travel between two stations in the east-west direction is 2 minutes.
Therefore, the time for which the train was running between M and N (excluding the stoppage time) =
20×2=40 minutes
Stoppage time at a junction is 2 minutes, while at the rest of the stations, it is 1 minute each.
Stoppage time for the train running between M and N =
(17×1)+(2×2)= 21 minutes
Therefore, total travel time = 40+21 = 61 minutes.
So the time by which Hari reaches N is 8:10 am + 61 minutes = 9:11 am
Priya can reach S from T via R or V.
Case 1:- T-V-S
In the east-west direction, the first train from P arrives at T at time = 6 am + (4×2)+(3×1)= 11 minutes = 6:11 am
Since T is a junction so this train will halt for 2 minutes at T and leave at 6:13.
Priya boards a east-west train then Priya will board a train for V from T at 10:33 am.
There are 9 stations between T and V
Travelling time between T and V = (10×2)+(9×1)=29 minutes
Therefore, Priya will reach V latest by 10:33 am + 29 minutes = 11:02 am
In the north-south direction, the first train from D arrives at V at time = 6 am + (3×3)+(2×1)= 11 minutes = 6:11 am
Since V is a junction so this train will halt for 2 minutes at V and leave at 6:13.
Since every 15 minutes, a train starts from D in the north-south direction, so the latest by which Priya will be able to board such a train from V is at 11:13 am.
There are 3 stations between V and S
Travelling time between R and S = (4×3)+((3×1))= 15 minutes
Time by which she reaches S = 11:13 +15 minutes = 11:28 am
Case 2:- T-R-S
In the north-south direction, the first train from B arrives at T at time = 6 am + (3×3)+(2×1)= 11 minutes = 6:11 am
Since T is a junction so this train will halt for 2 minutes at T and leave at 6:13.
Since every 15 minutes a train starts from P in the east-west direction so the latest by which Priya will be able to board such a train is at 10:28 am.
Now since she will be able to board a north-south train earlier than the east-west train so Priya will board a train for R from T at 10:28 am.
There are 3 stations between T and R
Travelling time between T and R = (4×3)+((3×1))= 15 minutes
Therefore, Priya will reach R latest by 10:43 am
In the east-west direction, the first train from M arrives at R at time = 6 am + (4×2)+(3×1)= 11 minutes = 6:11 am
Since R is a junction so this train will halt for 2 minutes at R and leave at 6:13.
Since every 10 minutes, a train starts from M in the east-west direction, so the latest by which Priya will be able to board such a train is at 10:43 am.
There are 9 stations between R and S
Travelling time between R and S = (10×2)+(9×1)=29 minutes
Time by which she reaches S = 10:43 +29 minutes = 11:12 am
We are getting shorter time in case 2. So 11:12 am is the answer
Travelling time between S and R = (10×2)+(9×1)=29 minutes
There is a stoppage of 2 minutes at R
Travelling time between R and B = (7×3)+(1×2)+(5×1)=28 minutes
In the north-south direction, the first train from A arrives at R at time = 6 am + (3×3)+(2×1) = 6:11 am.
Since R is a junction so this train will halt for 2 minutes at R and leave at 6:13.
Every 15 minutes, a train starts from A in the north-south direction.
The last train that leaves A will be at 12:00 am and it will leave R at 12:13 am, so Haripriya must reach R till 12:13 am.
Travelling time between S and R = (10×2)+(9×1)=29 minutes
So Haripriya must board the train at S by 11:44 pm
In the east-west direction, the first train from N arrives at S at time = 6 am + (6×2)+(5×1) = 6:17 am.
Since S is a junction so this train will halt for 2 minutes at S and leave at 6:19.
Every 10 minutes, a train starts from N in the east-west direction.
Therefore, Haripriya should board the train which leaves S at 11:39.
Travel time between A and B = (10×3)+(7×1)+(2×2)=41 minutes So if a train starts from 6 am from A to B, then the latest by which that train will start from B to A will be at 7 am, as in the north-south direction, a train starts from A and B every 15 minutes. So the total no. of trains required =
After completing a journey, a train must rest for 15 minutes at least before starting again.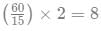
Travel time between A and B = (10×3)+(7×1)+(2×2)=41 minutes
After completing a journey, a train must rest for 15 minutes at least before starting again.
So if a train starts from 6 am from A to B, then the latest by which that train will start from B to A will be at 7 am, as in the north-south direction, a train starts from A and B every 15 minutes.
So the total no. of trains required for the north-south lines = 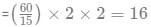
Travel time between M and N = (20×2)+(17×1)+(2×2)=61 minutes
After completing a journey, a train must rest for 15 minutes at least before starting again.
So if a train starts from 6 am from M to N, then the latest by which that train will start from N to M will be at 7:20 am, as in the east-west direction, a train starts from M and N every 15 minutes.
So the total no. of trains required for the east-west lines= 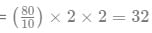
Total no. of trains required to service the city = 16+32 = 48
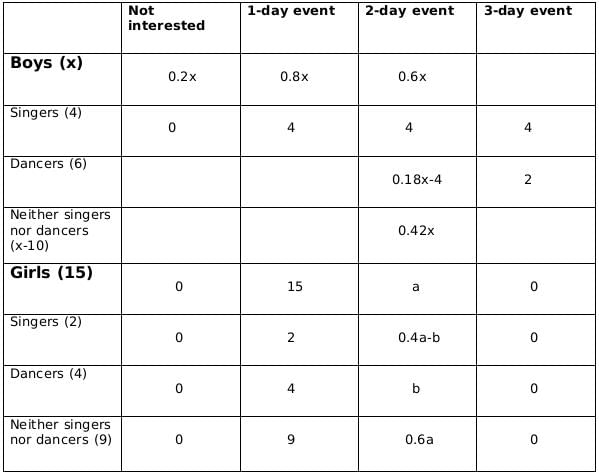
No. of girls = 15
Let the no. of boys be x
No. of singers = 6
No of boys who are singers = 4
Therefore, no of girls who are singers = 2
No of dancers = 10
No of boys who are dancers = 6
Therefore, no. of girls who are dancers = 4
No. of boys who are neither singers nor dancers = x-10
No. of girls who are neither singers nor dancers = 9
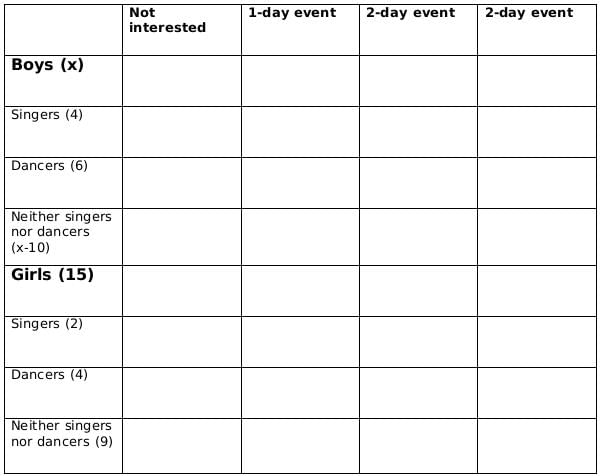
Now we fill the above table,
using statements 1 and 2, we get the following table
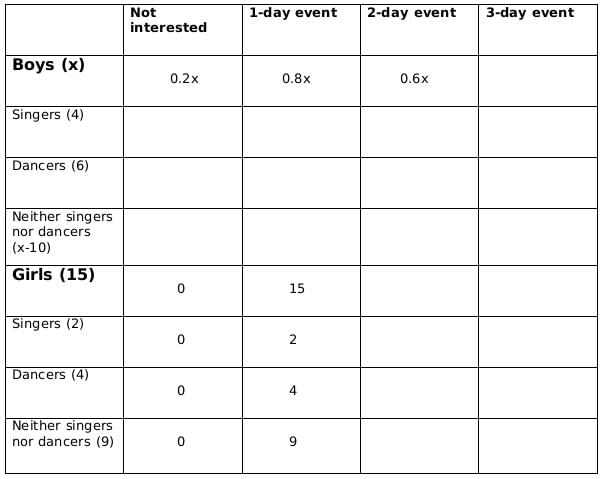
Let the number of girls who are interested in attending a 2-day event be a and the number of girls who are dancers and are interested in 2-day event be b.
Now using statements 3 and 4, we get
2 ≤ 0.18x − 4 ≤ 6
6 ≤ 0.18x ≤ 10
0.18x should be integer for which x should be a multiple of 50, and 0.18x lies between 6 and 10; therefore, the only possible value of x is 50.
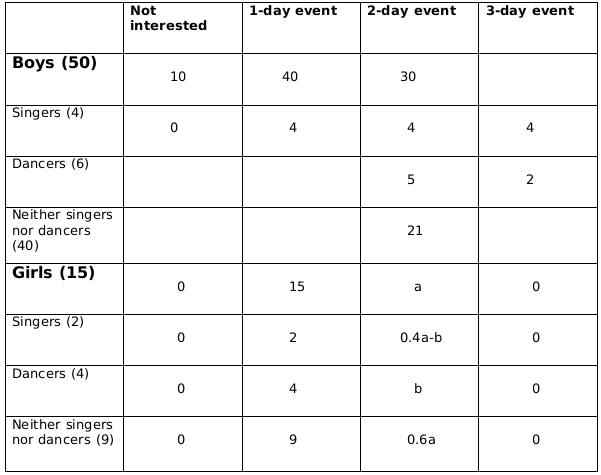
From statement 5, we can say that,
4+ 0.4a - b = 5+b +1
or, 0.4a = 2+2b
or, a = 5(1+b)
a should be a multiple of 5 as b is a whole number. So possible values of a can be 5, 10 or 15. Now, as the maximum value of b can be 4 and the maximum value of 0.4a-b can be 2, so the only possible value of a satisfying the conditions above is 5. If a= 5 then b=1.
No. of girls = 15
I. The number of boys who are interested in attending a 1-day event and are neither dancers nor singers.
II. The number of female dancers who are interested in attending a 1-day event.
Let the no. of boys be x
No. of singers = 6
No of boys who are singers = 4
Therefore, no of girls who are singers = 2
No of dancers = 10
No of boys who are dancers = 6
Therefore, no. of girls who are dancers = 4
No. of boys who are neither singers nor dancers = x-10
No. of girls who are neither singers nor dancers = 9

Now we fill the above table,
using statements 1 and 2, we get the following table

Let the number of girls who are interested in attending a 2-day event be a and the number of girls who are dancers and are interested in 2-day event be b.
Now using statements 3 and 4, we get

2 ≤ 0.18x − 4 ≤ 6
6 ≤ 0.18x ≤ 10
0.18x should be integer for which x should be a multiple of 50, and 0.18x lies between 6 and 10; therefore, the only possible value of x is 50.

From statement 5, we can say that,
4+ 0.4a - b = 5+b +1
or, 0.4a = 2+2b
or, a = 5(1+b)
a should be a multiple of 5 as b is a whole number. So possible values of a can be 5, 10 or 15. Now, as the maximum value of b can be 4 and the maximum value of 0.4a-b can be 2, so the only possible value of a satisfying the conditions above is 5. If a= 5 then b=1.

No. of girls = 15
Let the no. of boys be x
No. of singers = 6
No of boys who are singers = 4
Therefore, no of girls who are singers = 2
No of dancers = 10
No of boys who are dancers = 6
Therefore, no. of girls who are dancers = 4
No. of boys who are neither singers nor dancers = x-10
No. of girls who are neither singers nor dancers = 9

Now we fill the above table,
using statements 1 and 2, we get the following table

Let the number of girls who are interested in attending a 2-day event be a and the number of girls who are dancers and are interested in 2-day event be b.
Now using statements 3 and 4, we get

2 ≤ 0.18x − 4 ≤ 6
6 ≤ 0.18x ≤ 10
0.18x should be integer for which x should be a multiple of 50, and 0.18x lies between 6 and 10; therefore, the only possible value of x is 50.

From statement 5, we can say that,
4+ 0.4a - b = 5+b +1
or, 0.4a = 2+2b
or, a = 5(1+b)
a should be a multiple of 5 as b is a whole number. So possible values of a can be 5, 10 or 15. Now, as the maximum value of b can be 4 and the maximum value of 0.4a-b can be 2, so the only possible value of a satisfying the conditions above is 5. If a= 5 then b=1.

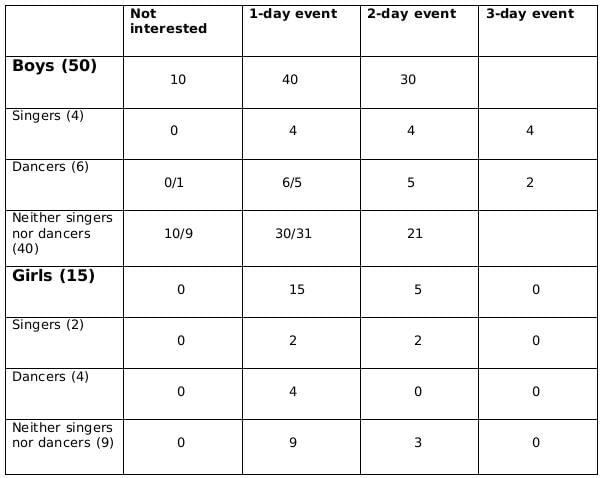
Total students interested in 2-day event = 30+5 = 35
Total students = 15 + 50 = 65
Fraction = 35 = 7/13
No. of girls = 15
Let the no. of boys be x
No. of singers = 6
No of boys who are singers = 4
Therefore, no of girls who are singers = 2
No of dancers = 10
No of boys who are dancers = 6
Therefore, no. of girls who are dancers = 4
No. of boys who are neither singers nor dancers = x-10
No. of girls who are neither singers nor dancers = 9

Now we fill the above table,
using statements 1 and 2, we get the following table

Let the number of girls who are interested in attending a 2-day event be a and the number of girls who are dancers and are interested in 2-day event be b.
Now using statements 3 and 4, we get

2 ≤ 0.18x − 4 ≤ 6
6 ≤ 0.18x ≤ 10
0.18x should be integer for which x should be a multiple of 50, and 0.18x lies between 6 and 10; therefore, the only possible value of x is 50.

From statement 5, we can say that,
4+ 0.4a - b = 5+b +1
or, 0.4a = 2+2b
or, a = 5(1+b)
a should be a multiple of 5 as b is a whole number. So possible values of a can be 5, 10 or 15. Now, as the maximum value of b can be 4 and the maximum value of 0.4a-b can be 2, so the only possible value of a satisfying the conditions above is 5. If a= 5 then b=1.

No. of girls = 15
Let the no. of boys be x
No. of singers = 6
No of boys who are singers = 4
Therefore, no of girls who are singers = 2
No of dancers = 10
No of boys who are dancers = 6
Therefore, no. of girls who are dancers = 4
No. of boys who are neither singers nor dancers = x-10
No. of girls who are neither singers nor dancers = 9

Now we fill the above table,
using statements 1 and 2, we get the following table

Let the number of girls who are interested in attending a 2-day event be a and the number of girls who are dancers and are interested in 2-day event be b.
Now using statements 3 and 4, we get

2 ≤ 0.18x − 4 ≤ 6
6 ≤ 0.18x ≤ 10
0.18x should be integer for which x should be a multiple of 50, and 0.18x lies between 6 and 10; therefore, the only possible value of x is 50.

From statement 5, we can say that,
4+ 0.4a - b = 5+b +1
or, 0.4a = 2+2b
or, a = 5(1+b)
a should be a multiple of 5 as b is a whole number. So possible values of a can be 5, 10 or 15. Now, as the maximum value of b can be 4 and the maximum value of 0.4a-b can be 2, so the only possible value of a satisfying the conditions above is 5. If a= 5 then b=1.

A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goals scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5). From statement 4 we know that Bimal scored 4 goals and since Harita scored more goals than Bimal so we can say that Harita scored 5 goals and the only case possible for total goals scored by each of the players is (1,2,4,5). Now using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which Bimal scored will be 5th, 6th and 7th matches as Harita scored in 4th and 8th matches and we get the following table:
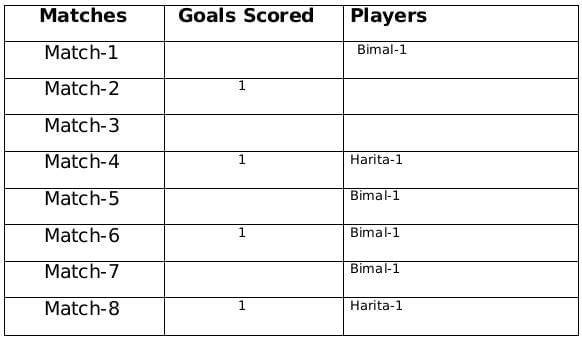
From statement 5 and 6, we can conclude that the highest number of goals were scored in Match 1.
Let the no. of goals scored in 3rd and 7th match be a each and no. of goals scored in 1st and 5th match be b and c respectively.
Therefore, 2a+b+c= 8
If a=1, then b+c=6 therefore possible solutions for b and c will be 2 and 4 only
If a=2, then b+c=4 therefore possible solution for b and c will be 1 and 3 only but since highest goals scored is in Match 1 so then no. of goals scored in match 1 must be 3 and Harita must have scored 3 goals in match 1 as Harita scored 5 goals in exactly 3 matches. Therefore, we can see this is not possible because then the no. of goals scored in Match 1 becomes 4.
Therefore the only possible solution is a=1, b=4 and c=2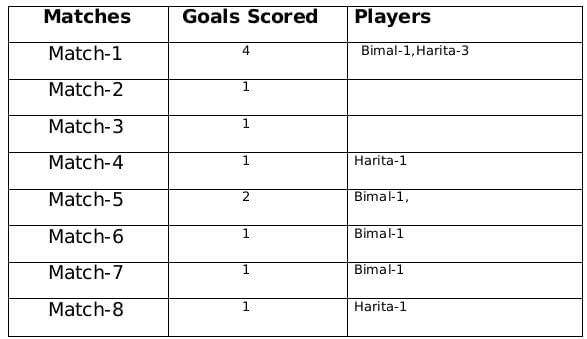
The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.
A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goals scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5). From statement 4 we know that Bimal scored 4 goals and since Harita scored more goals than Bimal so we can say that Harita scored 5 goals and the only case possible for total goals scored by each of the players is (1,2,4,5). Now using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which Bimal scored will be 5th, 6th and 7th matches as Harita scored in 4th and 8th matches and we get the following table:
From statement 5 and 6, we can conclude that the highest number of goals were scored in Match 1.
Let the no. of goals scored in 3rd and 7th match be a each and no. of goals scored in 1st and 5th match be b and c respectively.
Therefore, 2a+b+c= 8
If a=1, then b+c=6 therefore possible solutions for b and c will be 2 and 4 only
If a=2, then b+c=4 therefore possible solution for b and c will be 1 and 3 only but since highest goals scored is in Match 1 so then no. of goals scored in match 1 must be 3 and Harita must have scored 3 goals in match 1 as Harita scored 5 goals in exactly 3 matches. Therefore, we can see this is not possible because then the no. of goals scored in Match 1 becomes 4.
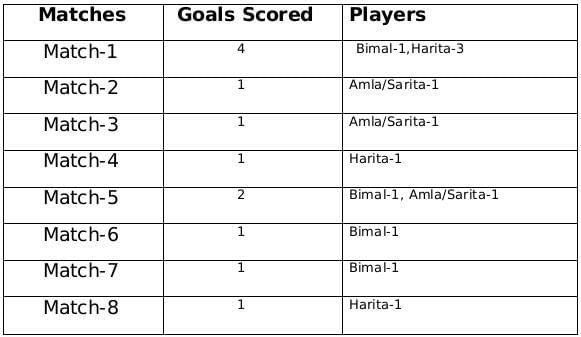
Therefore the only possible solution is a=1, b=4 and c=2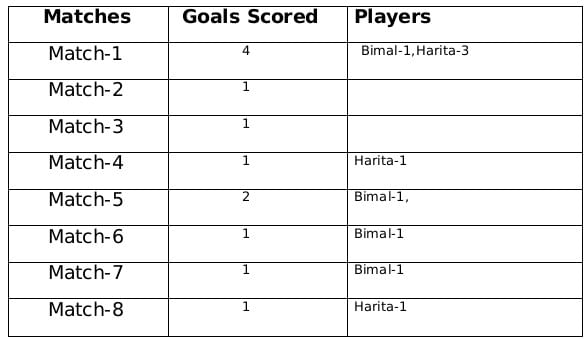
The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.
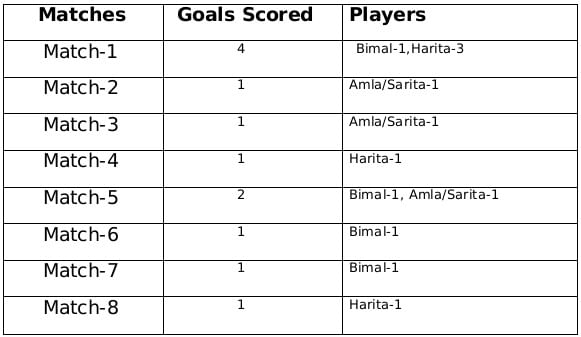
A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goals scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5). From statement 4 we know that Bimal scored 4 goals and since Harita scored more goals than Bimal so we can say that Harita scored 5 goals and the only case possible for total goals scored by each of the players is (1,2,4,5). Now using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which Bimal scored will be 5th, 6th and 7th matches as Harita scored in 4th and 8th matches and we get the following table:
Statement-1: Amla and Sarita never scored goals in the same match.
Statement-2: Harita and Sarita never scored goals in the same match.

From statement 5 and 6, we can conclude that the highest number of goals were scored in Match 1.
Let the no. of goals scored in 3rd and 7th match be a each and no. of goals scored in 1st and 5th match be b and c respectively.
Therefore, 2a+b+c= 8
If a=1, then b+c=6 therefore possible solutions for b and c will be 2 and 4 only
If a=2, then b+c=4 therefore possible solution for b and c will be 1 and 3 only but since highest goals scored is in Match 1 so then no. of goals scored in match 1 must be 3 and Harita must have scored 3 goals in match 1 as Harita scored 5 goals in exactly 3 matches. Therefore, we can see this is not possible because then the no. of goals scored in Match 1 becomes 4.
Therefore the only possible solution is a=1, b=4 and c=2
The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.

A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goals scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5). From statement 4 we know that Bimal scored 4 goals and since Harita scored more goals than Bimal so we can say that Harita scored 5 goals and the only case possible for total goals scored by each of the players is (1,2,4,5). Now using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which Bimal scored will be 5th, 6th and 7th matches as Harita scored in 4th and 8th matches and we get the following table:
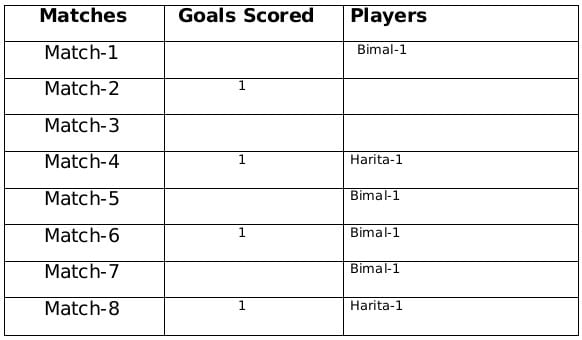
Statement-1: In every match at least one player scored a goal.
Statement-2: No two players scored goals in the same number of matches.

From statement 5 and 6, we can conclude that the highest number of goals were scored in Match 1.
Let the no. of goals scored in 3rd and 7th match be a each and no. of goals scored in 1st and 5th match be b and c respectively.
Therefore, 2a+b+c= 8
If a=1, then b+c=6 therefore possible solutions for b and c will be 2 and 4 only
If a=2, then b+c=4 therefore possible solution for b and c will be 1 and 3 only but since highest goals scored is in Match 1 so then no. of goals scored in match 1 must be 3 and Harita must have scored 3 goals in match 1 as Harita scored 5 goals in exactly 3 matches. Therefore, we can see this is not possible because then the no. of goals scored in Match 1 becomes 4.
Therefore the only possible solution is a=1, b=4 and c=2
The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.

A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goals scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5). From statement 4 we know that Bimal scored 4 goals and since Harita scored more goals than Bimal so we can say that Harita scored 5 goals and the only case possible for total goals scored by each of the players is (1,2,4,5). Now using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which Bimal scored will be 5th, 6th and 7th matches as Harita scored in 4th and 8th matches and we get the following table:
Statement-1: Amla scored goals in consecutive matches.
Statement-2: Sarita scored goals in consecutive matches.

From statement 5 and 6, we can conclude that the highest number of goals were scored in Match 1.
Let the no. of goals scored in 3rd and 7th match be a each and no. of goals scored in 1st and 5th match be b and c respectively.
Therefore, 2a+b+c= 8
If a=1, then b+c=6 therefore possible solutions for b and c will be 2 and 4 only
If a=2, then b+c=4 therefore possible solution for b and c will be 1 and 3 only but since highest goals scored is in Match 1 so then no. of goals scored in match 1 must be 3 and Harita must have scored 3 goals in match 1 as Harita scored 5 goals in exactly 3 matches. Therefore, we can see this is not possible because then the no. of goals scored in Match 1 becomes 4.
Therefore the only possible solution is a=1, b=4 and c=2
The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.


mock tests for examination
,Semester Notes
,Extra Questions
,MCQs
,video lectures
,Free
,Exam
,ppt
,past year papers
,Viva Questions
,shortcuts and tricks
,LRDI For CAT 2022 (Slot - 1)
,LRDI For CAT 2022 (Slot - 1)
,Objective type Questions
,practice quizzes
,Summary
,LRDI For CAT 2022 (Slot - 1)
,Previous Year Questions with Solutions
,Sample Paper
,Important questions
,study material
;




LRDI For CAT 2022 (Slot - 1) Free PDF Download
Importance of LRDI For CAT 2022 (Slot - 1)
LRDI For CAT 2022 (Slot - 1) Notes
LRDI For CAT 2022 (Slot - 1) CAT Questions
Study LRDI For CAT 2022 (Slot - 1) on the App

Contact Support
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|








