Laboratory Measurement of Permeability | Soil Mechanics - Civil Engineering (CE) PDF Download
Constant Head Flow
Constant head permeameter is recommended for coarse-grained soils only since for such soils, flow rate is measurable with adequate precision. As water flows through a sample of cross-section area A, steady total head drop h is measured across length L.

Permeability k is obtained from: 
Falling Head Flow
Falling head permeameter is recommended for fine-grained soils.

Total head h in standpipe of area a is allowed to fall. Hydraulic gradient varies with time. Heads h1 and h2 are measured at times t1 and t2. At any time t, flow through the soil sample of cross-sectional area A is
 ------------------------(1)
------------------------(1)
Flow in unit time through the standpipe of cross-sectional area a is
 ------------------------(2)
------------------------(2)
Equating (1) and (2) ,

Integrating between the limits,

Field Tests for Permeability
Field or in-situ measurement of permeability avoids the difficulties involved in obtaining and setting up undisturbed samples in a permeameter. It also provides information about bulk permeability, rather than merely the permeability of a small sample.
A field permeability test consists of pumping out water from a main well and observing the resulting drawdown surface of the original horizontal water table from at least two observation wells. When a steady state of flow is reached, the flow quantity and the levels in the observation wells are noted.
Two important field tests for determining permeability are: Unconfined flow pumping test, and confined flow pumping tes
Unconfined Flow Pumping Test

In this test, the pumping causes a drawdown in an unconfined (i.e. open surface) soil stratum, and generates a radial flow of water towards the pumping well. The steady-state heads h1 and h2 in observation wells at radii r1 and r2 are monitored till the flow rate q becomes steady.
The rate of radial flow through any cylindrical surface around the pumping well is equal to the amount of water pumped out. Consider such a surface having radius r, thickness dr and height h. The hydraulic gradient is

Area of flow, 
From Darcy's Law,

Arranging and integrating,


Confined Flow Pumping Test
Artesian conditions can exist in a aquifer of thickness D confined both above and below by impermeable strata. In this, the drawdown water table is above the upper surface of the aquifer.

For a cylindrical surface at radius r,

Integrating,


Permeability of Stratified Deposits
When a soil deposit consists of a number of horizontal layers having different permeabilities, the average value of permeability can be obtained separately for both vertical flow and horizontal flow, as kVand kH respectively.
Consider a stratified soil having horizontal layers of thickness H1, H2, H3, etc. with coefficients of permeability k1, k2, k3, etc.

For vertical flow
The flow rate q through each layer per unit area is the same.
q = q1 =q2
Let i be the equivalent hydraulic gradient over the total thickness H and let the hydraulic gradients in the layers be i1, i2, i3, etc. respectively.
 ............... where kV = Average vertical permeability
............... where kV = Average vertical permeability

The total head drop h across the layers is

Horizontal flow
When the flow is horizontal, the hydraulic gradient is the same in each layer, but the quantity of flow is different in each layer.

The total flow is

Considering unit width normal to the cross-section plane,

Worked Examples
Example 1: Determine the following:
(a) Equivalent coefficient of vertical permeability of the three layers
(b) The rate of flow per m2 of plan area
(c) The total head loss in the three layers

Solution:
(a)  = 1.33 x 10-3 cm/s
= 1.33 x 10-3 cm/s
(b) Considering an area A = 1 m2 =1 x 104 cm2
q = k.i.A =  = 7 x 10-4 x 0.25/2 x (1x104) = 0.875 cm3/s per m2 of plan area
= 7 x 10-4 x 0.25/2 x (1x104) = 0.875 cm3/s per m2 of plan area
(c) For continuity of flow, velocity is the same.
 where
where 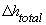 = total head loss in three layers
= total head loss in three layers

Example 2: For a field pumping test, a well was sunk through a horizontal stratum of sand 14.5 thick and underlain by a clay stratum.Two observation wells were sunk at horizontal distances of 16 m and 34 m respectively from the pumping well.The initial position of the water table was 2.2 m below ground level.
At a steady-state pumping rate of 1850 litres/min, the drawdowns in the observation wells were found to be 2.45 m and 1.20 m respectively. Calculate the coefficient of permeability of the sand.
Solution:



r1 = 16 m
r2 = 34 m
h1 = 14.5 - 2.2 - 2.45 = 9.85 m
h2= 14.5 - 2.2 - 1.2 = 11.1 m
k =  = 2.82 x 10-4 m/s = 1.41 x 10-2 cm/s
= 2.82 x 10-4 m/s = 1.41 x 10-2 cm/s
|
30 videos|76 docs|74 tests
|
FAQs on Laboratory Measurement of Permeability - Soil Mechanics - Civil Engineering (CE)
| 1. What is permeability and why is it important in civil engineering? |  |
| 2. How is permeability measured in a laboratory setting? |  |
| 3. What factors can influence the permeability of soil or rock? |  |
| 4. How does laboratory measurement of permeability differ from field measurements? |  |
| 5. What are the limitations of laboratory measurement of permeability? |  |

|
Explore Courses for Civil Engineering (CE) exam
|

|

















