Lag Compensator | Control Systems - Electrical Engineering (EE) PDF Download
Compensation Technique
In Control Engineering we generally focused on methods used to analyze the performance of a feedback system with a given set of parameters. The results of such analysis frequently show that the performance of the feedback system is unacceptable for a given application because of such deficiencies as low De-sensitivity, slow speed of response, or poor relative stability.
The process of modifying the system to improve the performance is called Compensation.
The required device added in control system to obtain the performance as per desired specification is known as Compensator.
1. Phase lead Compensation: A phase lead compensator improves transient response of the system. As the name implies, this network provides positive or leading phase shift of the output signal relative to the input signal at all frequencies. Lead-network parameters are usually selected to locate its singularities near the crossover frequency of the system being compensated. The positive phase shift of the network then improves the phase margin of the system.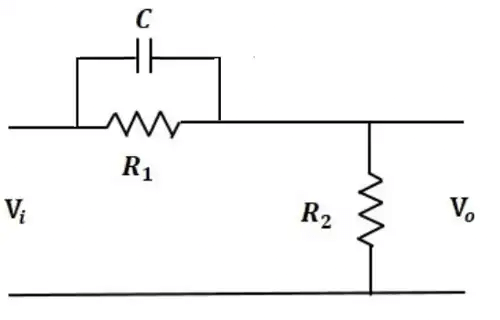 A phase-lead compensator has a transfer function of the form:
A phase-lead compensator has a transfer function of the form: 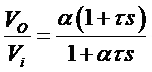
Where,
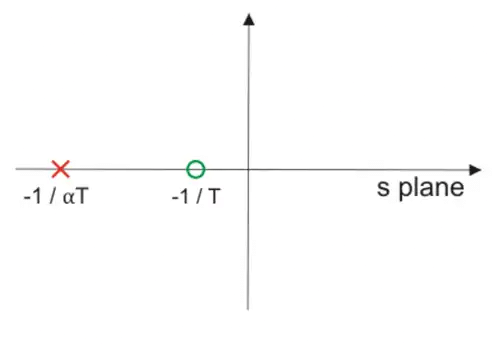
τ = R1C
α = R2 / R1 + R2
- A Lead Compensator is a high-pass filter.
- Zeros of the transfer function dominate in Phase Lead Compensation Technique.
2. Phase lag Compensation: Phase-lag systems are very common. These systems occur when an energy storage unit and an energy dissipator are combined. One example is the RC low pass. The phase-lag compensator has a negative phase angle and so is used to subtract phase from an uncompensated system.
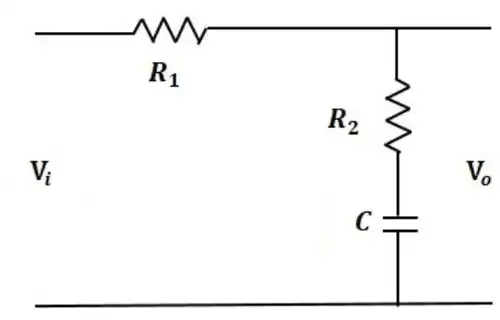 A phase-lag compensator has a transfer function of the form:
A phase-lag compensator has a transfer function of the form:
V0 / Vi = 1 + τs / 1 + βτs
Where,
τ = R2C
β = R1 + R2 / R2
Because the phase-lag compensator adds a negative phase angle to a system, the phase lag is not a useful effect of the compensation and does not provide a direct means of improving the phase margin. The phase-lag compensator does, however, reduce the gain and so can be used to lower the crossover frequency. A consequence of this is that, as usually the phase margin of the system is higher at the lower frequency, the stability can be improved.
In other words, there should not be much change in the location of the dominant poles. The pole of a phase lag compensator lies extremely close to the origin and its zero to the left of the pole and very near to it.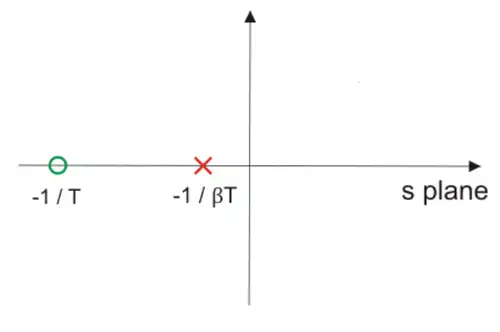
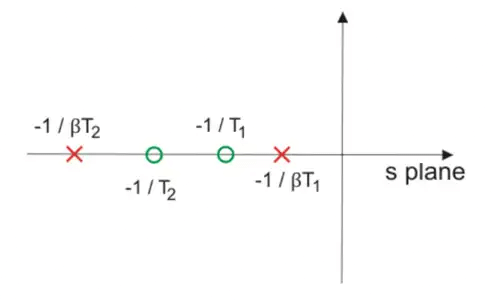
3. Phase lag lead Compensation: With single lag or lead compensation use we may not satisfied design specifications. For an unstable uncompensated system, lead compensation provides faster response but does not provide enough phase margin whereas lag compensation stabilize the system but does not provide enough bandwidth. So we need multiple compensators in cascade i.e. phase lag- lead compensation.
It act as a band stop filter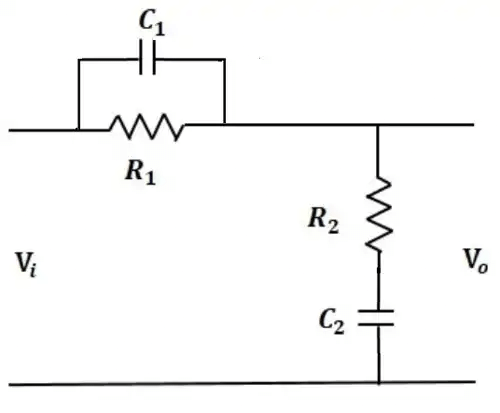
Controlling Action
- The controller (an analogue/digital circuit, and software), is trying to keep the controlled variable such as temperature, liquid level, motor velocity, robot joint angle, at a certain value called the set point (SP).
- A feedback control system does this by looking at the error (E) signal, which is the difference between where the controlled variable (called the process variable (PV)) is, and where it should be.
- Based upon the error signal, the controller decides the magnitude and the direction of the signal to the actuator.
The proportional (P), the integral (I), and the derivative (D), are all basic controllers.
Types of controllers
P, I, D, PI, PD, and PID controllers
1. Proportional Control
With proportional control, the actuator applies a corrective force that is proportional to the amount of error:
Outputp = Kp × E
Outputp = system output due to proportional control
Kp = proportional constant for the system called gain
E = error, the difference between where the controlled variable should be and where it is. E = SP – PV.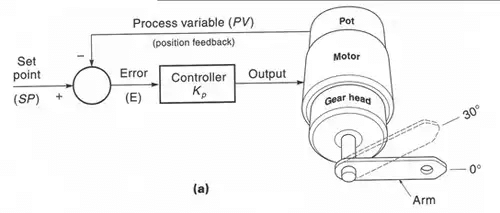 One way to decrease the steady-state error is to increase the system gain (Kp), but high Kp can lead to instability problems.
One way to decrease the steady-state error is to increase the system gain (Kp), but high Kp can lead to instability problems.
Increasing Kp independently without limit is not a sound control strategy.
2. Integral Control
The introduction of integral control in a control system can reduce the steady-state error to zero. Integral control applies a restoring force that is proportional to the sum of all past errors, multiplied by time.
OutputI = KI × ∑(E × Δt)
OutputI = controller output due to integral control
KI = integral gain constant (sometimes expressed as 1 / TI)
∑(E × Δt) = sum of all past errors (multiplied by time)
For a constant value of error ∑(E × Δt) will increase with time, causing the restoring force to get larger and larger.
Eventually, the restoring force will get large enough to overcome friction and move the controlled variable in a direction to eliminate the error.
3. Derivative Control
One solution to the overshoot problem is to include derivative control. Derivative control ‘applies the brakes,’ slowing the controlled variable just before it reaches its destination.
OutputD = controller output due to derivative control
KD = derivative gain constant
= error rate of change (slope of error curve)
4. Combining P, I and D controllers
As proportional, integral and derivative controllers have their individual strengths and weaknesses, they are often combined so that their strengths are maximised, whilst minimising their weaknesses. Many industrial controllers are a combination of P + I, or P + D, and are referred to as PI and PD controllers respectively.
5. PID control
A proportional–integral–derivative controller (PID controller) is a generic control loop feedback mechanism (controller) widely used in industrial control systems.
A PID controller attempts to correct the error between a measured process variable and a desired setpoint by calculating and then outputting a corrective action that can adjust the process accordingly.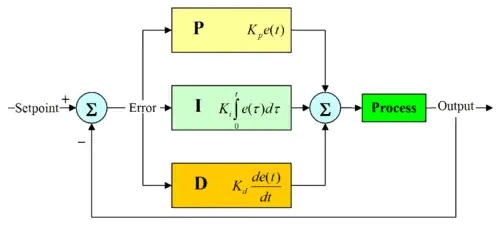 The foundation of the system is proportional control. Adding integral control provides a means to eliminate steady-state error, but increases overshoot. Derivative control increases stability by reducing the tendency to overshoot.
The foundation of the system is proportional control. Adding integral control provides a means to eliminate steady-state error, but increases overshoot. Derivative control increases stability by reducing the tendency to overshoot.
Simply adding together the three required control components generates the response of the PID system.
Output PID = output from PID controller
KP = proportional control gain
KI = integral control gain
KD = derivative control gain
E = error (deviation from set point)
∑(E × Δt) = sum of all past errors (area under the error/time curve)
(ΔE / Δt) = rate of change of error (slope of the error curve)
Equation is: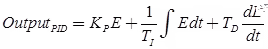
When you are designing a PID controller for a given system, follow the steps shown below to obtain the desired response.
- Obtain an open-loop response and determine what needs to be improved.
- Add a proportional control to improve the rise time.
- Add a derivative control to improve the overshoot.
- Add an integral control to eliminate the steady-state error.
- Adjust each of Kp, Ki, and Kd until you obtain a desired overall response.
The characteristics of P, I, and D controllers
- A proportional controller (Kp) will have the effect of reducing the rise time and will reduce, but never eliminate, the steady-state error.
- An integral control (Ki) will have the effect of eliminating the steady-state error, but it may make the transient response worse.
- A derivative control (Kd) will have the effect of increasing the stability of the system, reducing the overshoot, and improving the transient response.
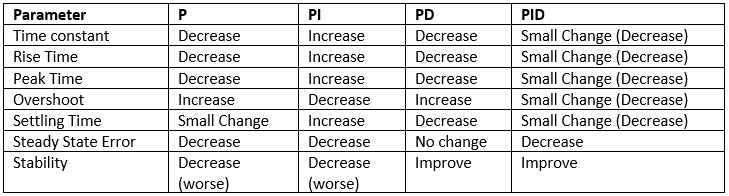
 Comparison Between P, PI and PID Controller.
Comparison Between P, PI and PID Controller.
|
53 videos|73 docs|40 tests
|
FAQs on Lag Compensator - Control Systems - Electrical Engineering (EE)
| 1. What is a lag compensator? |  |
| 2. How does a lag compensator work? |  |
| 3. When is a lag compensator used in control systems? |  |
| 4. Can a lag compensator make a system unstable? |  |
| 5. How is the design of a lag compensator determined? |  |