Irodov Solutions: Laws of Conservation of Energy, Momentum & Angular Momentum - 3 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
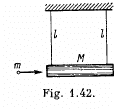
Q. 161. A cannon of mass M starts sliding freely down a smooth inclined plane at an angle a to the horizontal. After the cannon covered the distance l, a shot was fired, the shell leaving the cannon in the horizontal direction with a momentum p. As a consequence, the cannon stopped. Assuming the mass of the shell to be negligible, as compared to that of the cannon, determine the duration of the shot.
Ans. Velocity of cannon as well as that of shell equals 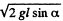 down the inclined plane taken as the positive x - axis. From the linear impulse momentum theorem in projection form along x - axis for the system (connon + shell) i.e. Δpx - Fx Δt :
down the inclined plane taken as the positive x - axis. From the linear impulse momentum theorem in projection form along x - axis for the system (connon + shell) i.e. Δpx - Fx Δt :
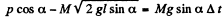 (as mass of the shell is neligible)
(as mass of the shell is neligible)
or, 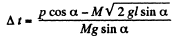
Q. 162. A horizontally flying bullet of mass m gets stuck in a body of mass M suspended by two identical threads of length l (Fig. 1.42). As a result, the threads swerve through an angle 0. Assuming m << M, find:
(a) the velocity of the bullet before striking the body;
(b) the fraction of the bullet's initial kinetic energy that turned into heat.
Ans. From conservation of momentum, for the system (bullet + body) along the initial direction of bullet
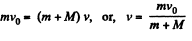
Q. 163. A body of mass M (Fig. 1.43) with a small disc of mass m placed on it rests on a smooth horizontal plane. The disc is set in motion in the horizontal direction with velocity v. To what height (relative to the initial level) will the disc rise after breaking off the body M? The friction is assumed to be absent.
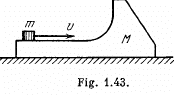
Ans. From conservation of momentum, along x-axis for the system (disc + body)
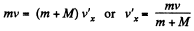 (1)
(1)
And from energy conservation, for the same system in the field of gravity :
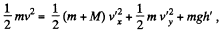
where h! is the height of break off point from initial level. So,
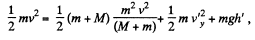 using (1)
using (1)
or, 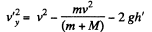
Also, if h" is the height of the disc, from the break-off point,
then, 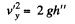
So, 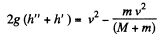
Hence, the total height, raised from the initial level

Q. 164. A small disc of mass m slides down a smooth hill of height h without initial velocity and gets onto a plank of mass M lying on the horizontal plane at the base of the hill (Fig. 1.44). Due to friction between the disc and the plank the disc slows down and, beginning with a certain moment, moves in one piece with the plank
(1) Find the total work performed by the friction forces in this process.
(2) Can it be stated that the result obtained does not depend on the choice of the reference frame?

Ans. (a) When the disc slides and comes to a plank, it has a velocity equal to 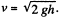 Due to friction between the disc and the plank the disc slows down and after some time the disc moves in one piece with the plank with velocity v' (say).
Due to friction between the disc and the plank the disc slows down and after some time the disc moves in one piece with the plank with velocity v' (say).
From the momentum conservation for the system (disc + plank) along horizontal towards right :
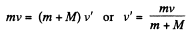
Now from the equation of the increment of total mechanical energy of a system :
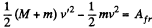
or, 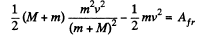
so, 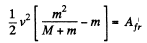
Hence, 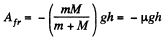

(b) We look at the problem from a frame in which the hill is moving (together with the disc on it) to the right with speed il Then in this frame the speed of the disc when it just gets onto the plank is, by the law of addition of velocities, 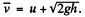 Similarly the common speed of the plank and the disc when they move together is
Similarly the common speed of the plank and the disc when they move together is

Then as above 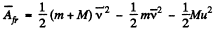
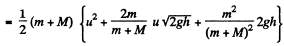
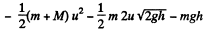
We see that  is independent of u and is in fact just - μ g h as in (a). Thus the result obtained does not depend on the choice of reference frame.
is independent of u and is in fact just - μ g h as in (a). Thus the result obtained does not depend on the choice of reference frame.
Do note however that it will be in correct to apply “conservation of enegy” formula in the frame in which the hill is moving. The energy carried by the hill is not negligible in this frame. See also the next problem.
Q. 165. A stone falls down without initial velocity from a height h onto the Earth's surface. The air drag assumed to be negligible, the stone hits the ground with velocity  relative to the Earth. Obtain the same formula in terms of the reference frame "falling" to the Earth with a constant velocity v0.
relative to the Earth. Obtain the same formula in terms of the reference frame "falling" to the Earth with a constant velocity v0.
Ans. In a frame moving relative to the earth, one has to include the kinetic energy of the earth as well as earth’s acceleration to be able to apply conservation of energy to the problem. In a reference frame falling to the earth with velocity v0, the stone is initially going up with velocity v0 and so is the earth. The final velocity of the stone is 0 = v0 - gt and that of the earth is 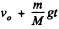 (M is the mass of the earth), from Newton’s third law, where t = time of fall. From conservation of energy
(M is the mass of the earth), from Newton’s third law, where t = time of fall. From conservation of energy
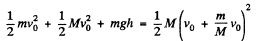
Hence 
Negecting 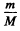 in comparison with 1, we get
in comparison with 1, we get
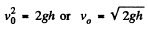 The point is this in earth’s rest frame the effect of earth’s accleration is of order
The point is this in earth’s rest frame the effect of earth’s accleration is of order 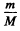 and can be neglected but in a frame moving with respect to the earth the effect of earth’s acceleration must be kept because it is of order one (i.e. large).
and can be neglected but in a frame moving with respect to the earth the effect of earth’s acceleration must be kept because it is of order one (i.e. large).
Q. 166. A particle of mass 1.0 g moving with velocity v1 = 3.0i - 2.0j experiences a perfectly inelastic collision with another particle of mass 2.0 g and velocity v2 = 4.0j — 6.0k. Find the velocity of the formed particle (both the vector v and its modulus), if the components of the vectors v1 and v2 are given in the SI units.
Ans. From conservation of momentum, for the closed system “both colliding particles”
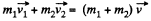
or, 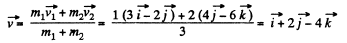
Hence 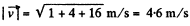
Q. 167. Find the increment of the kinetic energy of the closed system comprising two spheres of masses m1 and m2 due to their perfectly inelastic collision, if the initial velocities of the spheres were equal to v1 and v2.
Ans. For perfectly inelastic collision, in the C.M. frame, final kinetic energy of the colliding system (both spheres) becomes zero. Hence initial kinetic energy of the system in C.M. frame completely turns into the internal energy (Q) of the formed body. Hence

N ow from energy conservation 
In lab frame the same result is obtained as
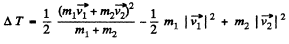
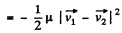
Q. 168. A particle of mass m1 experienced a perfectly elastic collision with a stationary particle of mass m2. What fraction of the kinetic energy does the striking particle lose, if
(a) it recoils at right angles to its original motion direction;
(b) the collision is a head-on one?
Ans. (a) Let the initial and final velocities of 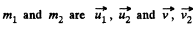 respectively.
respectively.
T hen from conservation o f momentum along horizontal and vertical directions, w e g et :

Squaring (1) and (2) and then adding them,


Now, from kinetic energy conservation,
 (3)
(3)
or, 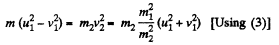
or, 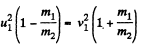
or,  (4)
(4)
So, fraction of kinetic energy lost by the particle 1,
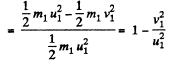
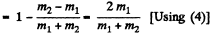 (5)
(5)
(b) When the collision occurs head on,
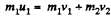
and from conservation of kinetic energy,
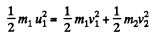
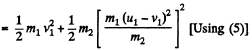
or, 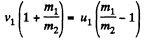
or, 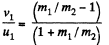 (6)
(6)
Fraction of kinetic energy, lost
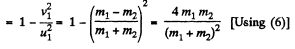
Q. 169. Particle 1 experiences a perfectly elastic collision with a stationary particle 2. Determine their mass ratio, if
(a) after a head-on collision the particles fly apart in the opposite directions with equal velocities;
(b) the particles fly apart symmetrically relative to the initial motion direction of particle 1 with the angle of divergence θ = 60°.
Ans. (a) When the particles fly apart in opposite direction with equal velocities (say v), then from conservatin of momentum,
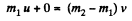 (1)
(1)
and from conservation of kinetic energy,
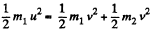
or, 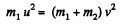 (2)
(2)
From Eq. (1) and (2),
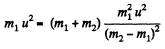
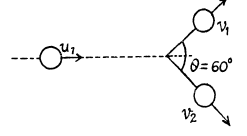
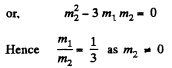
(b) When they fly apart symmetrically relative to the initial motion direction with the angle of divergence θ = 60°,
From conservation of momentum, along horizontal and vertical direction,
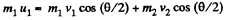 (1)
(1)
and 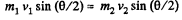
or,  (2)
(2)
Now, from conservation of kinetic energy,
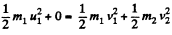 (3)
(3)
From (1) and (2),
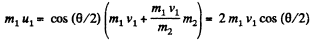
So, 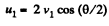 (4)
(4)
From (2), (3), and (4)
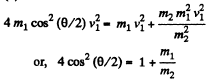
or, 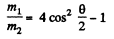
and putting the value of 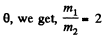
Q. 170. A ball moving translationally collides elastically with another, stationary, ball of the same mass. At the moment of impact the angle between the straight line passing through the centres of the balls and the direction of the initial motion of the striking ball is equal to α = 45°. Assuming the balls to be smooth, find the fraction η of the kinetic energy of the striking ball that turned into potential energy at the moment of the maximum deformation.
Ans. 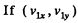 are the instantaneous velocity components of the incident ball and
are the instantaneous velocity components of the incident ball and 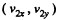 are the velocity components of the struck ball at the same moment, then since there are no external impulsive forces (i.e. other than the mutual interaction of the balls)
are the velocity components of the struck ball at the same moment, then since there are no external impulsive forces (i.e. other than the mutual interaction of the balls)
We have

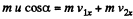
The impulsive force of mutual interaction satisfies
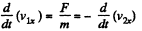
(F is along the x axis as the balls are smooth. Thus Y component of momentum is not transferred.) Since loss o f K.E. is stored as deformation energy D, we have
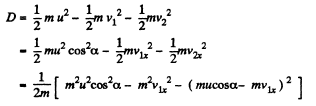
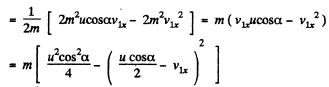
We see that D is maximum when
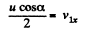
and 
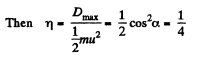
On substiuting α =45°
Q. 171. A shell flying with velocity v = 500 m/s bursts into three identical fragments so that the kinetic energy of the system increases η = 1.5 times. What maximum velocity can one of the fragments obtain?
Ans. From the conservation of linear momentum of the shell just before and after its fragmentation
 (1)
(1)
where  are the velocities of its fragments.
are the velocities of its fragments.
From the energy conservation  (2)
(2)
Now  (3)
(3)
where 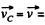 velocity of the C M . of the fragments the velocity of the shell. Obviously in the C.M. frame fbe linear momentum of a system is equal to zero, so
velocity of the C M . of the fragments the velocity of the shell. Obviously in the C.M. frame fbe linear momentum of a system is equal to zero, so
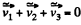 (4)
(4)
Using (3) and (4) in (2), we get
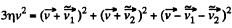
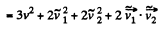
or, 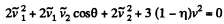 (5)
(5)
If we have had used 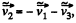 then Eq. 5 were contain
then Eq. 5 were contain  and so on.
and so on.
The problem being symmetrical we can look for the maximum of any one. Obviously it will be the same for each.

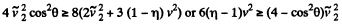
So, 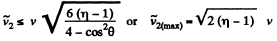
Hence 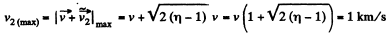
Thus owing to the symmetry
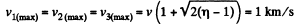
Q. 172. Particle 1 moving with velocity v = 10 m/s experienced a head-on collision with a stationary particle 2 of the same mass. As a result of the collision, the kinetic energy of the system decreased by η = 1.0%. Find the magnitude and direction of the velocity of particle 1 after the collision.
Ans. Since, the collision is head on, the particle 1 will continue moving along the same line as before the collision, but there will be a change in the magnitude of it’s velocity vector.
Let it starts moving with velocity v1 and particle 2 with v2 after collision, then from the conservation of momentum
mu = mv1 + mv2 or, u = v1 + v2 (1)
And from the condition, given,
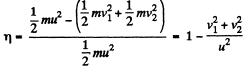
or, 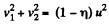 (2)
(2)
From (1) and (2),
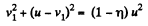
or, 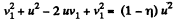
or, 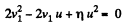
So, 
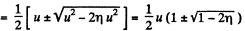
Positive sign gives the velocity of the 2nd particle which lies ahead. The negative sign is correct for v1.
So, 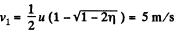 will continue moving in the same direction.
will continue moving in the same direction.
Note that 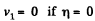 as it must.
as it must.
Q. 173. A particle of mass m having collided with a stationary particle of mass M deviated by an angle π/2 whereas the particle M recoiled at an angle θ = 30° to the direction of the initial motion of the particle tn. How much (in per cent) and in what way has the kinetic energy of this system changed after the collision, if M/m = 5.0?
Ans. Since, no external impulsive force is effective on the system “M + m”, its total momentum along any direction will remain conserved.
So from px = const.
 (1)
(1)
and from py = const
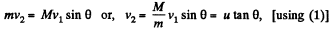
Final kinetic energy of the system
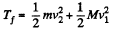
And initial kinetic energy of the system 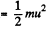
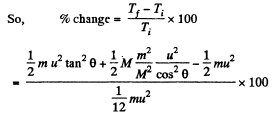
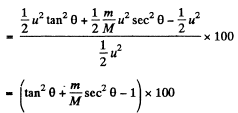
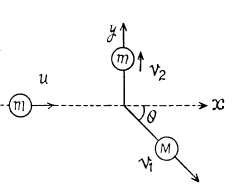
and putting the values of θ and m/M , we get % of change in kinetic energy = - 40 %
Q. 174. A closed system consists of two particles of masses m1 and m2 which move at right angles to each other with velocities v1 and v2. Find:
(a) the momentum of each particle and
(b) the total kinetic energy of the two particles in the reference frame fixed to their centre of inertia.
Ans. (a) Let the particles m1 and m2 move with velocities 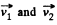 respectively. On the basis of solution of problem 1.147 (b)
respectively. On the basis of solution of problem 1.147 (b)
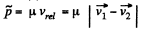
As 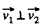
So, 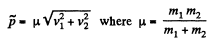
(b) Again from 1.147 (b)
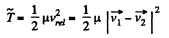
So, 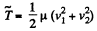
Q. 175. A particle of mass m1 collides elastically with a stationary particle of mass m2 (m1 > m2). Find the maximum angle through which the striking particle may deviate as a result of the collision.
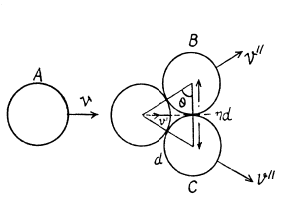
Ans. From conservation of momentum
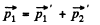
so 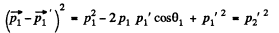
From conservation of eneigy
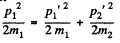
Eliminating p2’ we get
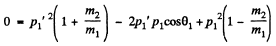
This quadratic equation for p1' has a real solution in terms of p1 and cos θ1 only if

or 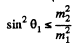
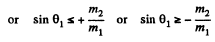
This clearly implies (since only + sign makes sense) that
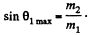
Q. 176. Three identical discs A, B, and C (Fig. 1.45) rest on a smooth horizontal plane. The disc A is set in motion with velocity v after which it experiences an elastic collision simultaneously with the discs B and C. The distance between the centres of the latter discs prior to the collision is η times greater than the diameter of each disc. Find the velocity of the disc A after the collision. At what value of η will the disc A recoil after the collision; stop; move on?

Ans. From the symmetry of the problem, the velocity of the disc A will be directed either in the initial direction or opposite to it just after the impact Let the velocity of the disc A after the collision be v' and be directed towards right after the collision. It is also clear from the symmetry of problem that the discs B and C have equal speed (say v") in the directions, shown. From the condition of the problem,
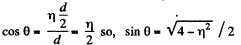 (1)
(1)
For the three discs, system, from the conservation of linear momentum in the symmetry direction (towards right)
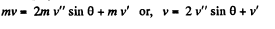 (2)
(2)
From the definition of the coefficeint of restitution, we have for the discs A and B (or C)
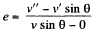
But e = 1, for perfectly elastic collision,
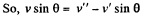 (2)
(2)
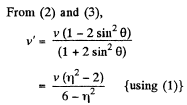
Hence we have,
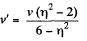
Therefore, the disc A will recoil if 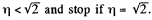
Note : One can write the equations of momentum conservation along the direction perpendicular to the initial direction of disc A and the consevation of kinetic energy instead of the equation of restitution.
Q. 177. A molecule collides with another, stationary, molecule of the same mass. Demonstrate that the angle of divergence
(a) equals 90° when the collision is ideally elastic;
(b) differs from 90° when the collision is inelastic
Ans. (a) Let a molecule comes with velocity 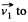 strike another stationary molecule and just after collision their velocities become
strike another stationary molecule and just after collision their velocities become 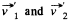 respectively. As the mass of the each molecule is same, conservation of linear momentum and conservation of kinetic energy for the system (both molecules) respectively gives :
respectively. As the mass of the each molecule is same, conservation of linear momentum and conservation of kinetic energy for the system (both molecules) respectively gives :
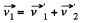
and 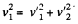
From the property of vector addition it is obvious from the obtained Eqs. that
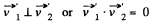
(b) Due to the loss of kinetic energy in inelastic collision 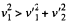
so, 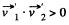 and therefore angle of divergence < 90°.
and therefore angle of divergence < 90°.
Q. 178. A rocket ejects a steady jet whose velocity is equal to u relative to the rocket. The gas discharge rate equals μ kg/s. Demonstrate that the rocket motion equation in this case takes the form 
where m is the mass of the rocket at a given moment, w is its acceleration, and F is the external force.
Ans. Suppose that at time tf the rocket has the mass m and the velocity 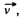 relative to the reference frame, employed. Now consider the inertial frame moving with the velocity that the rocket has at the given moment. In this reference frame, the momentum increament that the rocket & ejected gas system acquires during time dt is
relative to the reference frame, employed. Now consider the inertial frame moving with the velocity that the rocket has at the given moment. In this reference frame, the momentum increament that the rocket & ejected gas system acquires during time dt is
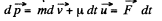
or, 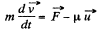
or, 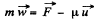
Q. 179. A rocket moves in the absence of external forces by ejecting a steady jet with velocity u constant relative to the rocket. Find the velocity v of the rocket at the moment when its mass is equal to m, if at the initial moment it possessed the mass m0 and its velocity was equal to zero. Make use of the formula given in the foregoing problem.
Ans. According to the question, 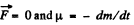 so the equation for this system becomes,
so the equation for this system becomes,
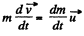
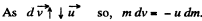
Integrating within the limits :
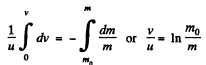
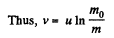
As 
Q. 180. Find the law according to which the mass of the rocket varies with time, when the rocket moves with a constant acceleration w, the external forces are absent, the gas escapes with a constant velocity u relative to the rocket, and its mass at the initial moment equals m0.
Ans. According to the question, 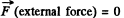
So, 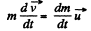
As 
so, in scalar form, 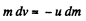
or,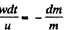
Integrating within the limits for m (t)
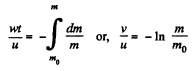
Hence, 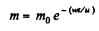
FAQs on Irodov Solutions: Laws of Conservation of Energy, Momentum & Angular Momentum - 3 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is the law of conservation of energy? |  |
| 2. How does the law of conservation of momentum apply to collisions? |  |
| 3. What is angular momentum and how is it conserved? |  |
| 4. How does the law of conservation of energy apply to different types of energy? |  |
| 5. Can the law of conservation of energy be violated? |  |

|
Explore Courses for JEE exam
|

|

















