DC Pandey Solutions: Laws of Motion - 2 | DC Pandey Solutions for JEE Physics PDF Download
Introductory Exercise 5.2
Q1. Three blocks of mass 1 kg, 4 kg and 2 kg are placed on a smooth horizontal plane as shown in figure. Find:
(a) the acceleration of the system,
(b) the normal force between 1 kg block and 4 kg block,
(c) the net force on 2 kg block.

Ans: (a) 10 ms-2 (b) 110 N (c) 20 N
Sol: Acceleration of system
= 10 m/s2
Let normal force between 1 kg block and 4 kg block = F1
∴ Net force on 1 kg block = 120 - N
∴
or 10 = 120 - F1
i.e., F1 = 110 N
Net force on 2 kg block = 2*a
= 2*10
=20 N
Q2. Two blocks of mass 2 kg and 4 kg are released from rest over a smooth inclined plane of inclination 30° as shown in figure. What is the normal force between the two blocks?

Ans: zero
Sol: As, 4 g sin 30° > 2 g sin 30°
The normal force between the two blocks will be zero.
Q3. What should be the acceleration ‘a’ of the box shown in figure so that the block of mass m exerts a force mg/4 on the floor of the box?
Ans: 3g/4
Sol:∴ N = mg/4
As lift is moving downward with acceleration a , the pseudo force on A will be ma acting in the upward direction. For the block to be at rest w.r.t. lift.
N + ma = mg
or
⇒
Q4. A plumb bob of mass 1 kg is hung from the ceiling of a train compartment. The train moves on an inclined plane with constant velocity. If the angle of incline is 30°. Find the angle made by the string with the normal to the ceiling. Also, find the tension in the string, (g = 10 m/s2)
Ans: 30°, ION
Sol: Angle made by the string with the normal to the ceiling = θ = 30°
As the train is moving with constant velocity no pseudo force will act on the plumb-bob.Tension in spring = mg
= 1*10
= 10 N
Q5. Repeat both parts of the above question, if the train moves with an acceleration a = g/2 up the plane.
Ans:
Sol: Pseudo force (= ma) on plumb-bob will be as shown in figureT cos φ = mg + ma cos (90° - θ)
i.e., T cos φ = mg + ma sin θ …(i)
and T sin φ = ma cos θ
Squaring and adding Eqs. (i) and (ii),
T2 = m2 g2 + m2 a2 sin2 θ + 2m2 ag sin θ + m2 a2 cos2 θ …(iii)
T2 = m2 g2 + m2 a2 + m2 ag (∴ θ = 30°)
or
Dividing Eq. (i) by Eq. (ii),
i.e.,
Q6. Two blocks of mass 1 kg and 2 kg are connected by a string AS of mass 1 kg. The blocks are placed on a smooth horizontal surface. Block of mass 1 kg is pulled by a horizontal force F of magnitude 8 N. Find the tension in the string at points A and B.
Ans: 4 N, 6 N
Sol:Net force on 1 kg mass = 8 - T2
∴ 8 - T2 = 1*2
⇒ T2 = 6 N
Net force on 1 kg block = T1
∴ T1 = 2a = 2*2 = 4 N
Introductory Exercise 5.3
Q1. In the arrangement shown in figure what should be the mass of block A, so that the system remains at rest? Neglect friction and mass of strings.
Ans: 3 kg
Sol: F = 2 g sin 30° = gFor the system to remain at rest
T2 = 2 g …(i)
T2 + F = T1 …(ii)
or T2 + g = T1 …[ii (a)]
T1 = mg …(iii)
Substituting the values of T1 and T2 from Eqs. (iii) and (i) in Eq. [ii(a)]
2 g + g = mg
i.e., m = 3 kg
Q2. In the arrangement shown in figure, find the ratio of tensions in the strings attached with 4 kg block and that with 1 kg block.
Ans: 4
Sol: As net downward force on the system is zero, the system will be in equilibrium∴ T1 = 4 g
and T2 = 1 g
∴
Q3. Two unequal masses of 1 kg and 2 kg are connected by a string going over a clamped light smooth pulley as shown in figure. The system is released from rest. The larger mass is stopped for a moment 1.0 s after the system is set in motion. Find the time elapsed before the string is tight again.
Ans: 1/3 s
Sol: 2 g - T = 2aT - 1 g = 1a
Adding above two equations
1 g = 3 a
∴ a = g/3
Velocity of 1kg block 1 section after the system is set in motion
v = 0 + at
On stopping 2 kg, the block of 1kg will go upwards with retardation g. Time ( t' ) taken by the 1 k g block to attain zero velocity will be given by the equation.
⇒
If the 2 kg block is stopped just for a moment (time being much-much less than 1/3 s), it will also start falling down when the stopping time ends.
Intime upward displacement of 1 kg block
Downward displacement of 2 kg block
As the two are just equal, the string will again become taut after time 1/3 s.
Q4. Two unequal masses of 1 kg and 2 kg are connected by an inextensible light string passing over a smooth pulley as shown in figure. A force F = 20 N is applied on 1 kg block. Find the acceleration of either block. (g = 10 m/s2).
Ans:
Sol: F + 1g - T = 1a … (i)and T - 2g = 2a …(ii)
Adding Eqs. (i) and (ii),
F - 1g = 3a
∴
Introductory Exercise 5.4
Q1. Consider the situation shown in figure. Both the pulleys and the string are light and all the surfaces are smooth.
(a) Find the acceleration of 1 kg block.
(b) Find the tension in the string.
(g = 10 m/s 2).
Ans: (a) 2g/3, (b) 10/3 N
Sol: 2T = 2*a … (i)and 1g - T = 2a …(ii)
Solving Eqs. (i) and (ii),
α = g/3
∴ Acceleration of 1 kg block
Tension in the string
Q2. Calculate the acceleration of either blocks and tension in the string shown in figure. The pulley and the string are light and all surfaces are smooth.
Ans:
Sol: Mg - T = Ma …(i)T = Ma …(ii)
Solving Eqs. (i) and (ii)
α = g/2
and T = Mg
Q3. Find the mass M so that it remains at rest in the adjoining figure. Both the pulley and string are light and friction is absent everywhere, (g = 10 m/s 2).
Ans: 4 . 8 kg
Sol: Block of mass M will be at rest ifT = Mg …(i)
For the motion of block of mass 3 kg....(ii)
For the motion of block of mass 2 kg....(iii)
Adding Eqs. (ii) and (iii),
g = 5a
i.e., α = g/5
Substituting above value of a in Eq. (iii),
T/2 = 2(g+a)
or
= 24g/5
Substituting value of above value of T in Eq. (i),
M = 24/5
= 4.8 kg
Q4. In figure assume that there is negligible friction between the blocks and table. Compute the tension in the cord connecting m2 and the pulley and acceleration of m2 if m1 = 300 g, m2 = 200g and F = 0.401V.
Ans:
Sol: T/2 = m1.2ai.e., T = 4 m1a …(i)
F - T = m2a …(ii)
or F - 4m1a = m2a
or
∴ T = 4 m1a
= 4*0.3* 2/7
= 2.4/7
= 12/35 N
Introductory Exercise 5.5
Ques 1: In figure m1 = 1 kg and m2 = 4 kg. Find the mass M o f the hanging block which will prevent the smaller block from slipping over the triangular block. All the surfaces are friction less and the strings and the pulleys are light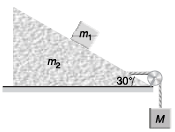
Note In exercises 2 to 4 the situations described take place in a box car which has initial velocity v = 0 but acceleration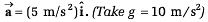
Ans: 6 .83 kg
Sol: Block on triangular block will not slip if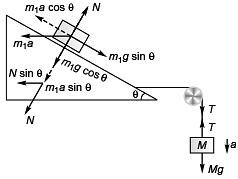
m1a cos θ= m1g sin θ
i.e., a = g tanθ …(i)
N = m1g cosθ + m1asinθ …(ii)
For the movement of triangular block
T - N sinθ = m2α …(iii)
For the movement of the block of mass M
Mg - T = Ma …(iv)
Adding Eqs. (iii) and (iv),
Mg - N sinθ = ( m2 + M )α
Substituting the value of N from Eq. (ii) in the above equation
Mg - (m1g cosθ + m1α sinθ) sinθ
=( m2α + Mα)
i.e., M (g - α) = m1g cosθ sinθ + (m2 + m1 sin2θ)α
Substituting value of a from Eq. (i) in the above equation,
M(1 - tanθ) = m1 cosθ sinθ + ( m2 + m1 sin2 θ) tanθ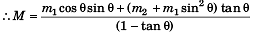
Substituting θ = 30° , m1 = 1 kg and m2 = 4 kg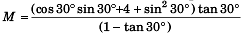
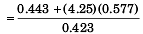
= 6.82 kg
Ques 2: A 2 kg object is slid along the friction less floor with initial velocity (10 m/s)î (a) Describe the motion of the object relative to car (b) when does the object reach its original position relative to the box car.
Ans: (a) x = x0 + 10t - 2.5t2 , v = 10 - 5t (b) t = 4s
Sol: (a) Using 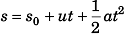
Displacement of block at time t relative to car would be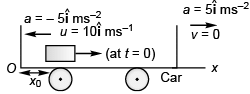
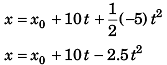
Velocity of block at time t (relative to car) will be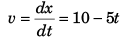
(b) Time (t) for the block to arrive at the original position (i.e., x = x0) relative to car
x0 = x0 + 10 t - 2.5 t2
⇒ t = 4s
Ques 3: A 2 kg object is slid along the friction less floor with initial transverse velocity (10 m/s) . Describe the motion (a) in car’s frame (b) in ground frame.
. Describe the motion (a) in car’s frame (b) in ground frame.
Ans: (a) x = x0 - 2.5t2, z = z0 + 10t, vx = - 5t, vz = 10 ms-1
(b) x = x0, z = z0 + 10t, vx = 0, vz = 10 ms-1
Sol: (a) In car’s frame position of object at time t would be given by
In car’s frame
x = x0 + 0*t + 1/2(-5)t2
i.e., x = x0 - 2.5 t2 …(i)
and z = z + 10t …(ii)
Velocity of the object at time t would be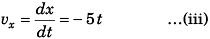
and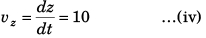
(b) In ground frame the position of the object at time t would be given by
In ground frame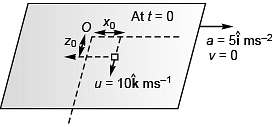
x = x0
and z = z0 + 10t
Velocity of the object at time t would be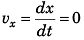
ans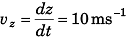
Ques 4: A 2 kg object is slid along a rough floor (coefficient of sliding friction = 0.3) with initial velocity (10 m/s)î. Describe the motion of the object relative to car assuming that the coefficient of static friction is greater than 0.5.
Ans: x = x0 + 10f - 4t2 , K = 10 - 8 t for 0<f<1.25 s object stops at t = 1.25 s and remains at rest relative to car.
Sol: m = 2 kg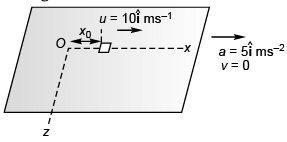
Normal force on object = mg
Maximum sliding friction = μsmg
= 0.3*2*10 = 6 N
Deceleration due to friction = 6/2 =3 m/s2
Deceleration due to pseudo force = 5 m/s2
∴ Net deceleration = (3 + 5) m/s2
= 8 m/s2
∴ Displacement of object at any time t (relative to car)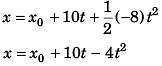
Thus, velocity of object at any time t (relative to car)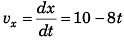
The object will stop moving relative to car when
10 - 8t = 0 i.e., t = 1.25s
∴ vx = 10 - 8t for 0<t<1.25 s
Ques 5: A block is placed on an inclined plane as shown in figure. What must be the frictional force between block and incline if the block is not to slide along the incline when the incline is accelerating to the right at 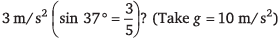

Ans: 9/25 mg
Sol: For block not to slide the frictional force ( f ) would be given by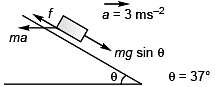
f + ma cosθ = mg sinθ
or
f = mg sinθ - ma cosθ
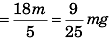
FAQs on DC Pandey Solutions: Laws of Motion - 2 - DC Pandey Solutions for JEE Physics
| 1. What are the laws of motion? |  |
| 2. What is the significance of the laws of motion? |  |
| 3. How do the laws of motion relate to everyday life? |  |
| 4. How are the laws of motion different from each other? |  |
| 5. How do the laws of motion apply to space travel? |  |

|
Explore Courses for JEE exam
|

|



 ∴ N = mg/4
∴ N = mg/4

 Tension in spring = mg
Tension in spring = mg
 T cos φ = mg + ma cos (90° - θ)
T cos φ = mg + ma cos (90° - θ)








 Net force on 1 kg mass = 8 - T2
Net force on 1 kg mass = 8 - T2 For the system to remain at rest
For the system to remain at rest ∴ T1 = 4 g
∴ T1 = 4 g
 T - 1 g = 1a
T - 1 g = 1a


 time upward displacement of 1 kg block
time upward displacement of 1 kg block


 and T - 2g = 2a …(ii)
and T - 2g = 2a …(ii)
 and 1g - T = 2a …(ii)
and 1g - T = 2a …(ii)


 T = Ma …(ii)
T = Ma …(ii) T = Mg …(i)
T = Mg …(i) ....(ii)
....(ii) ....(iii)
....(iii)

 i.e., T = 4 m1a …(i)
i.e., T = 4 m1a …(i)



















