Class 6 Exam > Class 6 Notes > Maths Olympiad Class 6 > Learning Poster: Prime Factorisation
Learning Poster: Prime Factorisation | Maths Olympiad Class 6 PDF Download
The document Learning Poster: Prime Factorisation | Maths Olympiad Class 6 is a part of the Class 6 Course Maths Olympiad Class 6.
All you need of Class 6 at this link: Class 6
|
31 videos|122 docs|60 tests
|
FAQs on Learning Poster: Prime Factorisation - Maths Olympiad Class 6
| 1. What is prime factorization and why is it important? |  |
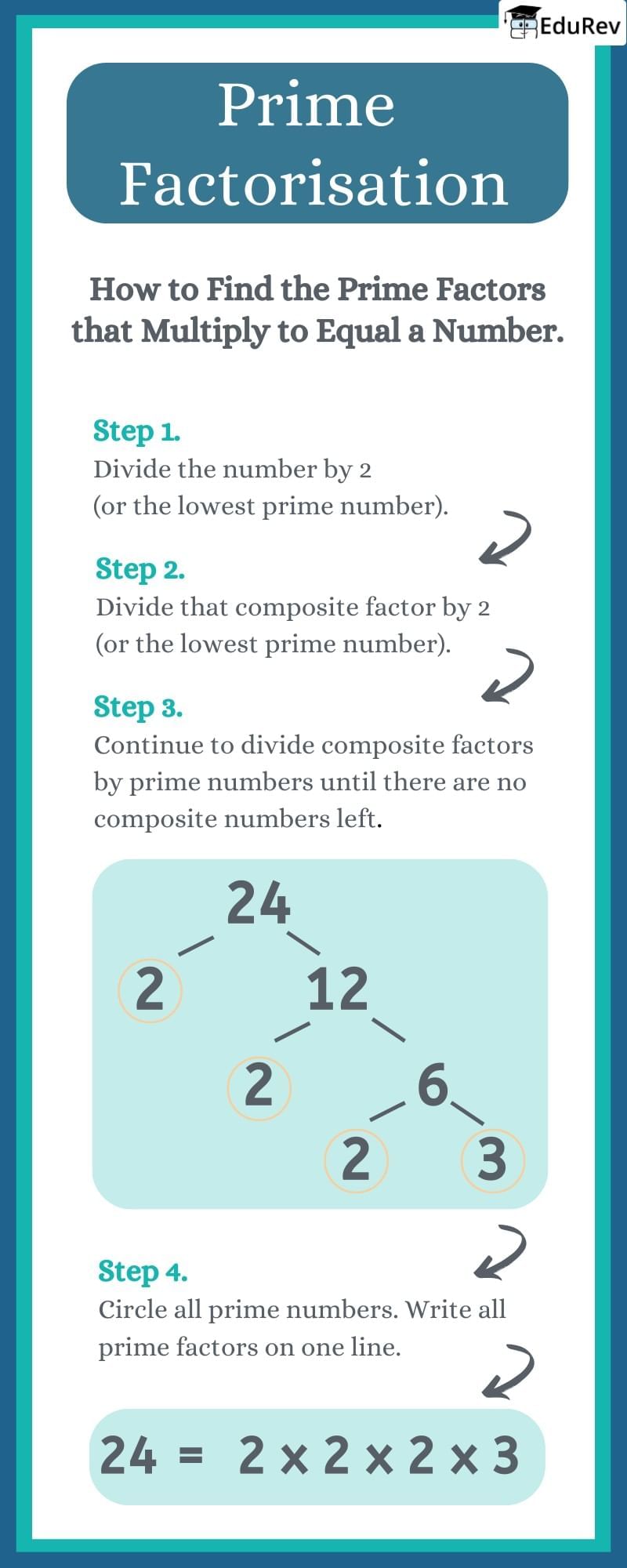
Ans.Prime factorization is the process of expressing a number as the product of its prime factors. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. Prime factorization is important because it helps simplify fractions, find the greatest common divisor (GCD), and the least common multiple (LCM) of numbers. Understanding prime factorization also lays the foundation for more advanced mathematical concepts.
| 2. How do you find the prime factors of a number? | |
Ans.To find the prime factors of a number, you can use the following method: Start by dividing the number by the smallest prime number, which is 2. If the number is even, divide it by 2 until it is no longer divisible. If it is odd, move to the next smallest prime number (3, 5, 7, etc.) and continue the process. Record each prime number you used to divide. Repeat until you cannot divide anymore, and the resulting quotient will be 1. The prime factors are the prime numbers you recorded during the process.
| 3. Can all numbers be expressed as a product of prime factors? | |
Ans.Yes, all natural numbers greater than 1 can be expressed as a product of prime factors. This concept is known as the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 either is a prime number or can be uniquely factored into prime numbers, regardless of the order of the factors. For example, the number 28 can be expressed as 2 x 2 x 7 (or 2² x 7).
| 4. What is the difference between prime and composite numbers? | |
Ans.Prime numbers are natural numbers greater than 1 that have exactly two distinct positive divisors: 1 and the number itself. In contrast, composite numbers are natural numbers greater than 1 that have more than two positive divisors. For example, 5 is a prime number because it can only be divided by 1 and 5, while 6 is a composite number because it can be divided by 1, 2, 3, and 6.
| 5. How is prime factorization used in real life? | |
Ans.Prime factorization has several practical applications in real life. It is used in computer science for algorithms related to encryption and coding. It helps in simplifying fractions in cooking or budgeting by finding common denominators. Additionally, prime factorization is essential in areas such as cryptography, where secure communications rely on the difficulty of factoring large numbers into their prime components, thus ensuring data protection.
About this Document
Sep 22, 2025
Last updated
Related Exams
Document Description: Learning Poster: Prime Factorisation for Class 6 2025 is part of Maths Olympiad Class 6 preparation.
The notes and questions for Learning Poster: Prime Factorisation have been prepared according to the Class 6 exam syllabus. Information about Learning Poster: Prime Factorisation covers topics
like and Learning Poster: Prime Factorisation Example, for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Learning Poster: Prime Factorisation.
Introduction of Learning Poster: Prime Factorisation in English is available as part of our Maths Olympiad Class 6
for Class 6 & Learning Poster: Prime Factorisation in Hindi for Maths Olympiad Class 6 course.
Download more important topics related with notes, lectures and mock test series for Class 6
Exam by signing up for free. Class 6: Learning Poster: Prime Factorisation | Maths Olympiad Class 6
Description
Full syllabus notes, lecture & questions for Learning Poster: Prime Factorisation | Maths Olympiad Class 6 - Class 6 | Plus excerises question with solution to help you revise complete syllabus for Maths Olympiad Class 6 | Best notes, free PDF download
Information about Learning Poster: Prime Factorisation
In this doc you can find the meaning of Learning Poster: Prime Factorisation defined & explained in the simplest way possible. Besides explaining types of
Learning Poster: Prime Factorisation theory, EduRev gives you an ample number of questions to practice Learning Poster: Prime Factorisation tests, examples and also practice Class 6
tests
Related Searches
past year papers
,practice quizzes
,Learning Poster: Prime Factorisation | Maths Olympiad Class 6
,mock tests for examination
,Semester Notes
,Extra Questions
,video lectures
,Free
,ppt
,Learning Poster: Prime Factorisation | Maths Olympiad Class 6
,Sample Paper
,Learning Poster: Prime Factorisation | Maths Olympiad Class 6
,Important questions
,Exam
,study material
,Summary
,Previous Year Questions with Solutions
,MCQs
,Objective type Questions
,shortcuts and tricks
,Viva Questions
,
Additional Information about Learning Poster: Prime Factorisation for Class 6 Preparation
Learning Poster: Prime Factorisation Free PDF Download
The Learning Poster: Prime Factorisation is an invaluable resource that delves deep into the core of the Class 6 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Learning Poster: Prime Factorisation now and kickstart your journey towards success in the Class 6 exam.
Importance of Learning Poster: Prime Factorisation
The importance of Learning Poster: Prime Factorisation cannot be overstated, especially for Class 6 aspirants.
This document holds the key to success in the Class 6 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Learning Poster: Prime Factorisation Notes
Learning Poster: Prime Factorisation Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Learning Poster: Prime Factorisation.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Learning Poster: Prime Factorisation Notes on EduRev are your ultimate resource for success.
Learning Poster: Prime Factorisation Class 6 Questions
The "Learning Poster: Prime Factorisation Class 6 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 6 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Learning Poster: Prime Factorisation on the App
Students of Class 6 can study Learning Poster: Prime Factorisation alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Learning Poster: Prime Factorisation,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Learning Poster: Prime Factorisation is prepared as per the latest Class 6 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup