Class 8 Exam > Class 8 Notes > Mathematics Class 8- New NCERT (Ganita Prakash) > Let's Learn: Prime Factorisation
Let's Learn: Prime Factorisation | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
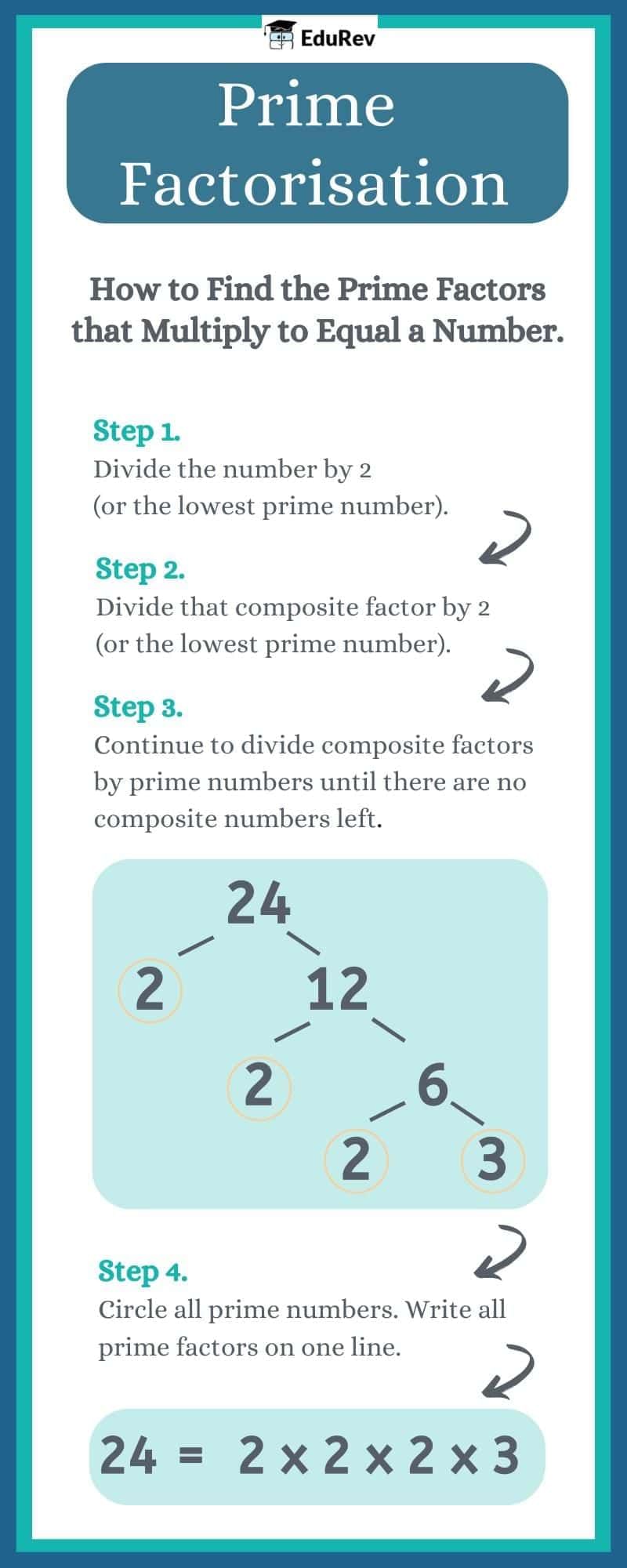
The document Let's Learn: Prime Factorisation | Mathematics Class 8- New NCERT (Ganita Prakash) is a part of the Class 8 Course Mathematics Class 8- New NCERT (Ganita Prakash).
All you need of Class 8 at this link: Class 8
|
21 videos|177 docs|11 tests
|
FAQs on Let's Learn: Prime Factorisation - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What is prime factorization and why is it important? |  |
Ans.Prime factorization is the process of breaking down a composite number into the product of its prime factors. A prime number is a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers. Prime factorization is important because it helps in understanding the properties of numbers, simplifying fractions, and finding the greatest common divisor (GCD) and least common multiple (LCM) of numbers.
| 2. How can I find the prime factorization of a number? | |
Ans.To find the prime factorization of a number, you can use methods such as trial division, where you divide the number by the smallest prime number (2, 3, 5, etc.) and continue dividing until you reach 1. Alternatively, you can use a factor tree method, where you break the number down into factors and continue to factor each composite number until all factors are prime.
| 3. Can prime factorization be used for large numbers? | |
Ans.Yes, prime factorization can be used for large numbers, but it can be more complex and time-consuming. Methods like using algorithms or computer software can assist in finding the prime factorization of larger numbers efficiently. However, for educational purposes, smaller numbers are typically used to illustrate the concept.
| 4. What is the significance of the Fundamental Theorem of Arithmetic in relation to prime factorization? | |
Ans.The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be expressed uniquely as a product of prime numbers, up to the order of the factors. This theorem underlines the importance of prime factorization because it assures that the prime factors of a number are consistent and provides a foundation for number theory.
| 5. How does prime factorization help in finding the GCD and LCM of two numbers? | |
Ans.Prime factorization helps in finding the greatest common divisor (GCD) and least common multiple (LCM) of two numbers by allowing you to compare their prime factors. The GCD can be found by multiplying the lowest powers of all common prime factors, while the LCM can be calculated by multiplying the highest powers of all prime factors present in both numbers. This systematic approach simplifies the process significantly.
About this Document
Sep 21, 2025
Last updated
Related Exams
Document Description: Let's Learn: Prime Factorisation for Class 8 2025 is part of Mathematics Class 8- New NCERT (Ganita Prakash) preparation.
The notes and questions for Let's Learn: Prime Factorisation have been prepared according to the Class 8 exam syllabus. Information about Let's Learn: Prime Factorisation covers topics
like and Let's Learn: Prime Factorisation Example, for Class 8 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Let's Learn: Prime Factorisation.
Introduction of Let's Learn: Prime Factorisation in English is available as part of our Mathematics Class 8- New NCERT (Ganita Prakash)
for Class 8 & Let's Learn: Prime Factorisation in Hindi for Mathematics Class 8- New NCERT (Ganita Prakash) course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: Let's Learn: Prime Factorisation | Mathematics Class 8- New NCERT (Ganita Prakash)
Description
Full syllabus notes, lecture & questions for Let's Learn: Prime Factorisation | Mathematics Class 8- New NCERT (Ganita Prakash) - Class 8 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 8- New NCERT (Ganita Prakash) | Best notes, free PDF download
Information about Let's Learn: Prime Factorisation
In this doc you can find the meaning of Let's Learn: Prime Factorisation defined & explained in the simplest way possible. Besides explaining types of
Let's Learn: Prime Factorisation theory, EduRev gives you an ample number of questions to practice Let's Learn: Prime Factorisation tests, examples and also practice Class 8
tests
Related Searches
Semester Notes
,Viva Questions
,Free
,Important questions
,mock tests for examination
,MCQs
,Exam
,past year papers
,Let's Learn: Prime Factorisation | Mathematics Class 8- New NCERT (Ganita Prakash)
,Objective type Questions
,ppt
,Sample Paper
,video lectures
,shortcuts and tricks
,Summary
,Extra Questions
,Previous Year Questions with Solutions
,study material
,Let's Learn: Prime Factorisation | Mathematics Class 8- New NCERT (Ganita Prakash)
,Let's Learn: Prime Factorisation | Mathematics Class 8- New NCERT (Ganita Prakash)
,practice quizzes
;
Additional Information about Let's Learn: Prime Factorisation for Class 8 Preparation
Let's Learn: Prime Factorisation Free PDF Download
The Let's Learn: Prime Factorisation is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Let's Learn: Prime Factorisation now and kickstart your journey towards success in the Class 8 exam.
Importance of Let's Learn: Prime Factorisation
The importance of Let's Learn: Prime Factorisation cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Let's Learn: Prime Factorisation Notes
Let's Learn: Prime Factorisation Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Let's Learn: Prime Factorisation.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Let's Learn: Prime Factorisation Notes on EduRev are your ultimate resource for success.
Let's Learn: Prime Factorisation Class 8 Questions
The "Let's Learn: Prime Factorisation Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Let's Learn: Prime Factorisation on the App
Students of Class 8 can study Let's Learn: Prime Factorisation alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Let's Learn: Prime Factorisation,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Let's Learn: Prime Factorisation is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup