Class 5 Exam > Class 5 Notes > Mathematics (Maths Mela) Class 5 - New NCERT > Let's Learn: Types of Symmetry
Let's Learn: Types of Symmetry | Mathematics (Maths Mela) Class 5 - New NCERT PDF Download
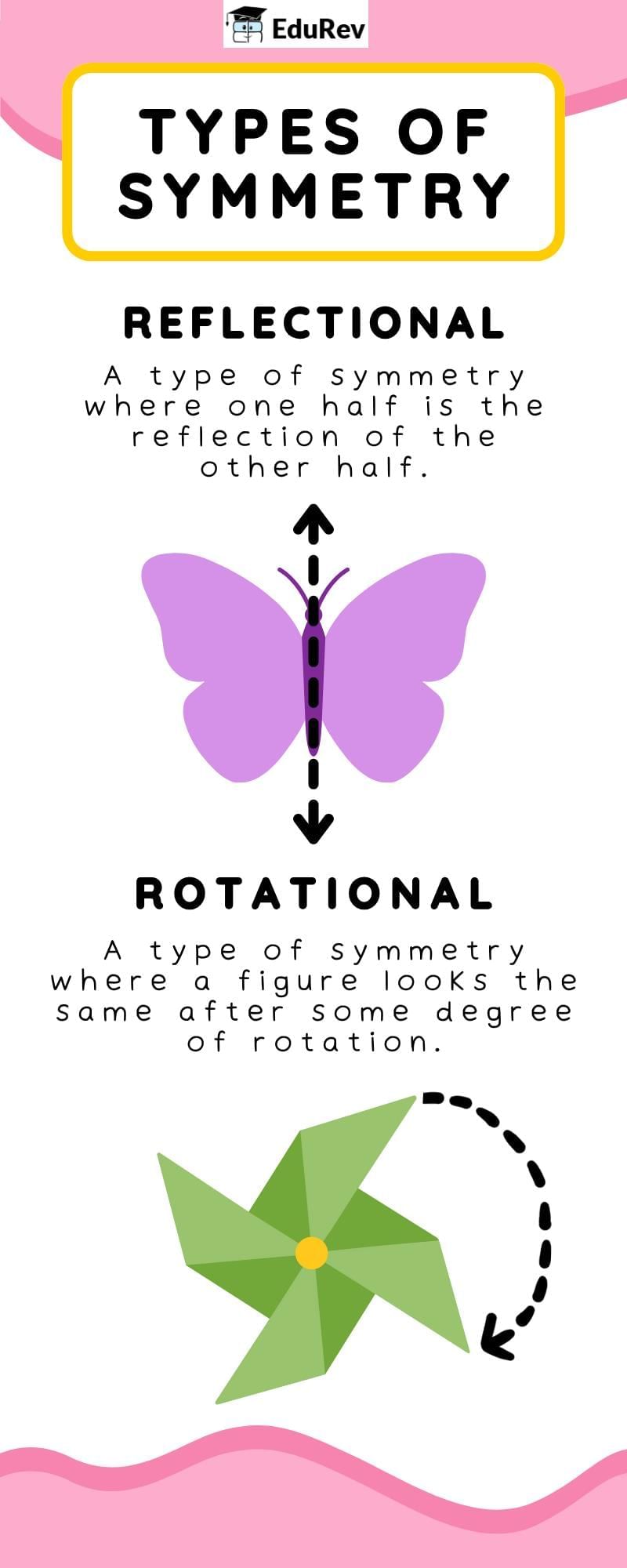
The document Let's Learn: Types of Symmetry | Mathematics (Maths Mela) Class 5 - New NCERT is a part of the Class 5 Course Mathematics (Maths Mela) Class 5 - New NCERT.
All you need of Class 5 at this link: Class 5
|
35 videos|276 docs|7 tests
|
FAQs on Let's Learn: Types of Symmetry - Mathematics (Maths Mela) Class 5 - New NCERT
| 1. What are the different types of symmetry? |  |
Ans. There are several types of symmetry, including:
1. <b>Reflective Symmetry (Mirror Symmetry)</b>: This occurs when one half of an object is a mirror image of the other half. An example is a butterfly.
2. <b>Rotational Symmetry</b>: This is when an object looks the same after a certain amount of rotation. For instance, a star shape can have rotational symmetry.
3. <b>Translational Symmetry</b>: This happens when an object can be moved (translated) along a certain direction and still look the same. A tiled floor is a good example.
4. <b>Radial Symmetry</b>: This type of symmetry is found in objects that can be divided into similar sections around a central point, like a wheel or a flower.
5. <b>Glide Reflection Symmetry</b>: This is a combination of reflection and translation, where an object is reflected over a line and then slid along that line.
| 2. How can we identify symmetry in everyday objects? | |
Ans. To identify symmetry in everyday objects, you can look for specific characteristics:
- <b>Mirror Lines</b>: Check if you can draw a line through the object where both sides are identical. This indicates reflective symmetry.
- <b>Rotation</b>: Try to rotate the object around a point. If it looks the same after a certain angle, it has rotational symmetry.
- <b>Tiling Patterns</b>: Observe patterns on walls or floors. If the pattern can be repeated without any gaps or overlaps, it shows translational symmetry.
- <b>Shapes of Nature</b>: Many natural objects, such as leaves and flowers, exhibit radial symmetry. Look for how many identical parts surround a central point.
| 3. Why is symmetry important in art and design? | |
Ans. Symmetry is important in art and design for several reasons:
1. <b>Aesthetic Appeal</b>: Symmetrical designs are often perceived as more beautiful and balanced, attracting viewers' attention.
2. <b>Organization</b>: Symmetry helps organize visual elements, making it easier for viewers to navigate and understand the artwork or design.
3. <b>Symbolism</b>: Many cultures associate symmetry with harmony and perfection, which can convey deeper meanings in artistic expressions.
4. <b>Functionality</b>: In design, symmetry can enhance the functionality of objects, like furniture or architecture, making them more stable and easier to use.
| 4. Can you give examples of symmetry in nature? | |
Ans. Yes, symmetry is prevalent in nature. Some examples include:
- <b>Flowers</b>: Many flowers, such as daisies and tulips, exhibit radial symmetry with petals arranged around a central point.
- <b>Animals</b>: Creatures like starfish display radial symmetry, while most mammals, including humans, have bilateral symmetry.
- <b>Snowflakes</b>: Each snowflake has a unique pattern but generally exhibits six-fold rotational symmetry.
- <b>Leaves</b>: The arrangement of veins in leaves often shows reflective symmetry, with one side mirroring the other.
| 5. How does symmetry relate to mathematics? | |
Ans. Symmetry is deeply connected to mathematics in various ways:
1. <b>Geometric Shapes</b>: Many geometric shapes, like squares and circles, have defined lines of symmetry that can be analyzed mathematically.
2. <b>Patterns and Transformations</b>: The study of symmetry involves understanding transformations such as rotation, reflection, and translation, which are fundamental concepts in geometry.
3. <b>Algebraic Symmetry</b>: In algebra, symmetry can help solve equations and understand functions through symmetry properties.
4. <b>Fractals</b>: Certain mathematical sets, like fractals, exhibit self-similarity, a form of symmetry that repeats at different scales.
About this Document
Sep 19, 2025
Last updated
Related Exams
Document Description: Let's Learn: Types of Symmetry for Class 5 2025 is part of Mathematics (Maths Mela) Class 5 - New NCERT preparation.
The notes and questions for Let's Learn: Types of Symmetry have been prepared according to the Class 5 exam syllabus. Information about Let's Learn: Types of Symmetry covers topics
like and Let's Learn: Types of Symmetry Example, for Class 5 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Let's Learn: Types of Symmetry.
Introduction of Let's Learn: Types of Symmetry in English is available as part of our Mathematics (Maths Mela) Class 5 - New NCERT
for Class 5 & Let's Learn: Types of Symmetry in Hindi for Mathematics (Maths Mela) Class 5 - New NCERT course.
Download more important topics related with notes, lectures and mock test series for Class 5
Exam by signing up for free. Class 5: Let's Learn: Types of Symmetry | Mathematics (Maths Mela) Class 5 - New NCERT
Description
Full syllabus notes, lecture & questions for Let's Learn: Types of Symmetry | Mathematics (Maths Mela) Class 5 - New NCERT - Class 5 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths Mela) Class 5 - New NCERT | Best notes, free PDF download
Information about Let's Learn: Types of Symmetry
In this doc you can find the meaning of Let's Learn: Types of Symmetry defined & explained in the simplest way possible. Besides explaining types of
Let's Learn: Types of Symmetry theory, EduRev gives you an ample number of questions to practice Let's Learn: Types of Symmetry tests, examples and also practice Class 5
tests
Related Searches
Free
,Semester Notes
,Viva Questions
,MCQs
,mock tests for examination
,Important questions
,Exam
,past year papers
,practice quizzes
,Let's Learn: Types of Symmetry | Mathematics (Maths Mela) Class 5 - New NCERT
,Let's Learn: Types of Symmetry | Mathematics (Maths Mela) Class 5 - New NCERT
,Sample Paper
,Let's Learn: Types of Symmetry | Mathematics (Maths Mela) Class 5 - New NCERT
,Extra Questions
,shortcuts and tricks
,Previous Year Questions with Solutions
,video lectures
,Objective type Questions
,ppt
,study material
,Summary
;
Additional Information about Let's Learn: Types of Symmetry for Class 5 Preparation
Let's Learn: Types of Symmetry Free PDF Download
The Let's Learn: Types of Symmetry is an invaluable resource that delves deep into the core of the Class 5 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Let's Learn: Types of Symmetry now and kickstart your journey towards success in the Class 5 exam.
Importance of Let's Learn: Types of Symmetry
The importance of Let's Learn: Types of Symmetry cannot be overstated, especially for Class 5 aspirants.
This document holds the key to success in the Class 5 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Let's Learn: Types of Symmetry Notes
Let's Learn: Types of Symmetry Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Let's Learn: Types of Symmetry.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Let's Learn: Types of Symmetry Notes on EduRev are your ultimate resource for success.
Let's Learn: Types of Symmetry Class 5 Questions
The "Let's Learn: Types of Symmetry Class 5 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 5 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Let's Learn: Types of Symmetry on the App
Students of Class 5 can study Let's Learn: Types of Symmetry alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Let's Learn: Types of Symmetry,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Let's Learn: Types of Symmetry is prepared as per the latest Class 5 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup