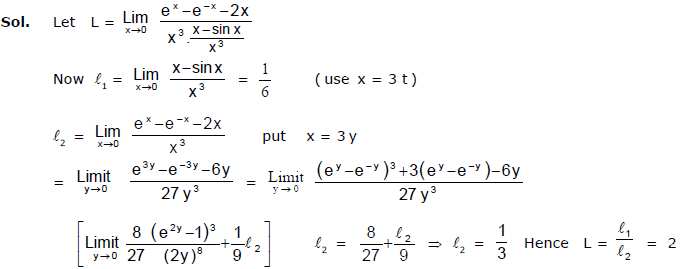Class 11 Exam > Class 11 Notes > Limit of exponential functions - Limits and Derivatives, Class 11, Mathematics
Limit of exponential functions - Limits and Derivatives, Class 11, Mathematics PDF Download
(3) Limit of exponential functions
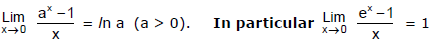
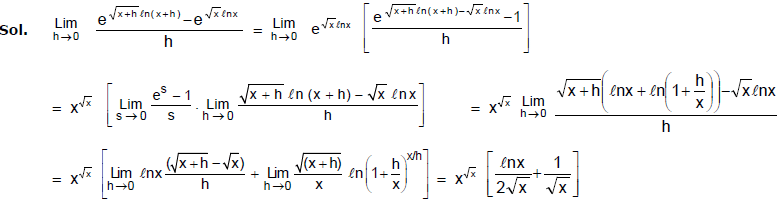
Ex.26 Evaluate 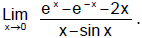

Ex.27 Evaluate 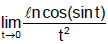
Sol.

FAQs on Limit of exponential functions - Limits and Derivatives, Class 11, Mathematics
| 1. What is the limit of an exponential function as it approaches infinity? |  |
| 2. What is the limit of an exponential function as it approaches negative infinity? |  |
Ans. Similar to the limit as x approaches infinity, the limit of an exponential function as it approaches negative infinity also depends on the base. If the base is greater than 1, the exponential function will decrease without bound as x approaches negative infinity, and the limit will be 0. If the base is between 0 and 1, the exponential function will approach positive infinity as x approaches negative infinity, and the limit will be positive infinity.
| 3. How do you find the limit of an exponential function at a specific value of x? |  |
Ans. To find the limit of an exponential function at a specific value of x, you can directly substitute that value into the function and evaluate it. For example, if you want to find the limit of the exponential function f(x) = 2^x as x approaches 3, you can substitute x = 3 into the function and calculate f(3) = 2^3 = 8.
| 4. Can an exponential function have a negative limit? |  |
Ans. No, an exponential function cannot have a negative limit. As x approaches either positive infinity or negative infinity, the exponential function will either approach positive infinity or 0, depending on the base of the function. The limit can never be negative.
| 5. What happens to the limit of an exponential function if the base is equal to 1? |  |
Ans. If the base of an exponential function is equal to 1, the limit of the function will always be 1, regardless of the value of x. This is because any number raised to the power of 0 is equal to 1.
Download as PDF
Top Courses for Class 11
Related Searches