Limits, Continuity & Differentiability | Engineering Mathematics - Engineering Mathematics PDF Download
| Table of contents |

|
| Limits |

|
| L’Hospital Rule |

|
| Continuity |

|
| Differentiability |

|
| Solved Numericals |

|
Limits, continuity, and differentiability are fundamental concepts in calculus that provide a structured way to analyze and model the behavior of functions.
Limits allow us to understand how a function behaves as its input approaches a specific value, laying the groundwork for calculus.
Continuity ensures a function behaves predictably without breaks or abrupt changes, which is crucial for real-world systems. Differentiability quantifies how a function changes, enabling the study of rates, such as speed or growth.
Together, these concepts form the backbone of mathematical analysis, providing tools for optimizing systems, solving engineering problems, and interpreting dynamic phenomena logically and systematically.
Limits
- For a function f(x), the limit of the function at a point x = a is the value the function achieves at a point that is very close to x = a.
- Mathematically, ,
- Let f(x) be a function defined on an open interval around a, except at a itself.
Then, the limit of f(x) as x approaches a is L if for every ε > 0, there exists a δ > 0 such that
0 < |x - a| < δ ⇒ |f(x) - L| < ε - This can be expressed as limx → a f(x) = L

- As is clear from the above figure, the limit can be approached from either sides of the number line i.e. the limit can be defined in terms of a number less that a or in terms of a number greater than a.
Two types of limits
- Left Hand Limit
If the limit is defined in terms of a number which is less than a then the limit is said to be the left hand limit. It is denoted as which is equivalent to x = a - h where h > 0 and h → 0.
which is equivalent to x = a - h where h > 0 and h → 0. - Right Hand Limit
If the limit is defined in terms of a number which is greater than a then the limit is said to be the right hand limit. It is denoted as x → a+ which is equivalent to x = a + h where h > 0 and h → 0.
Existence of Limit
The limit of a function f(x) at x = a exists only when its left hand limit and right hand limit exist and are equal and have a finite value i.e.
Some Common Limits
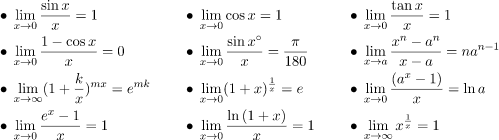
L’Hospital Rule
- If the given limit
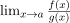 is of the form 0/0 or ∞/∞ i.e. both f(x) and g(x) are 0 or both f(x) and g(x) are ∞ then the limit can be solved by L’Hospital Rule.
is of the form 0/0 or ∞/∞ i.e. both f(x) and g(x) are 0 or both f(x) and g(x) are ∞ then the limit can be solved by L’Hospital Rule.
If the limit is of the form described above, then the L’Hospital Rule says that –
where f'(x) and g'(x) obtained by differentiating f(x) and g(x).
If after differentitating, the form still exists, then the rule can be applied continuously until the form is changed.
Example 1: Evaluate 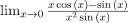
 View Answer
View Answer 
Sol: The limit is of the form 0/0, Using L’Hospital Rule and differentiating numerator and denominator



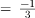
Example 2: Evaluate 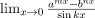
 View Answer
View Answer 



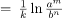
Continuity
A function is said to be continuous over a range if it’s graph is a single unbroken curve.
Formally,
A real valued function f(x) is said to be continuous at a point in the domain if –
in the domain if – f(x) exists and is equal to
f(x) exists and is equal to  .
.
If a function f(x) is continuous at  then-
then-
Functions that are not continuous are said to be discontinuous
Example: For what value of λ is the function defined by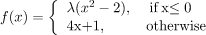
continuous at x = 0?
Solution: For the function to be continuous the left hand limit, right hand limit and the value of the function at that point must be equal.
Value of function at x=0

Right hand limit-
= 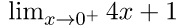
= 1
RHL equals value of function at 0-
-2λ = 1
λ = -1 / 2
Differentiability
- The derivative of a real-valued function f(x) wrt x is the function f'(x) and is defined as
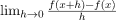
- A function is said to be differentiable if the derivative of the function exists at all points of its domain.
- For checking the differentiability of a function at point x = c,
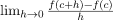 must exist.
must exist. - If a function is differentiable at a point, then it is also continuous at that point.
Note: If a function is continuous at a point does not imply that the function is also differentiable at that point. For example, f(x) = |x| is continuous at x = 0 but it is not differentiable at that point.
Solved Numericals
Q1: Value of the limit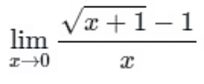 (a) 1
(a) 1
(b) 2
(c) 1/2
(d) More than one of the above
 View Answer
View Answer 
Ans: (c)
Sol: 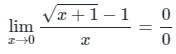
which is an indeterminate form.
So, by using L’Hospital’s Rule, on differentiating numerator and the denominator separately we get,
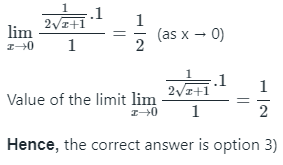
Q2: If 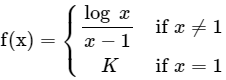 is continuous at x = 1, then the value of K is
is continuous at x = 1, then the value of K is
(a) 0
(b) -1
(c) 1
(d) More than one of the above
 View Answer
View Answer 
Ans: (c)
Sol:
Since, the function is continuous at x = 1.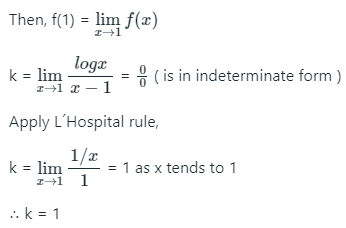
Hence, the correct answer is option 3)
Q3: If f(4) = 4, f '(4) = 1, then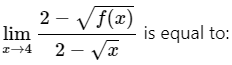
(a) -2
(b) 2
(c) 1
(d) More than one of the above
 View Answer
View Answer 
Ans: (c)
Sol:
Given: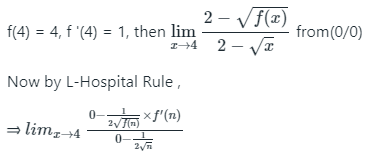
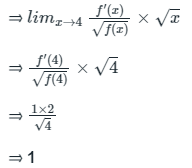
|
65 videos|129 docs|94 tests
|
FAQs on Limits, Continuity & Differentiability - Engineering Mathematics - Engineering Mathematics
| 1. What is the L'Hospital Rule and when is it used in calculus? |  |
| 2. How does continuity differ from differentiability in calculus? |  |
| 3. Can a function be continuous but not differentiable at a point? |  |
| 4. How can limits help in understanding the behavior of functions near certain points? |  |
| 5. What are the conditions for a function to be differentiable at a point? |  |
















