JEE Exam > JEE Notes > Mock Tests for JEE Main and Advanced 2025 > Revision Notes - Limits
Limits Class 11 Notes Maths
- Limit of a function may be a finite or an infinite number.
- If limx→a f(x) = ∞, it just implies that the function f(x) tends to assume extremely large positive values in the vicinity of x = a i.e. limx→0 1/|x|= ∞.
- A function is said to be indeterminate at any point if it acquires one of the following values at that particular point:
0/0, 0 × ∞, ∞/∞, ∞-∞, 00, 1∞, ∞0. - The 0/0 form is the standard indeterminate form.
- The point ‘∞’ cannot be plotted on the paper. It is just a symbol and not a number.
Infinity (∞) does not obey the laws of elementary algebra.
1. ∞ + ∞ = ∞
2. ∞ x ∞ = ∞
3. (a/∞) = 0, if a is finite
4. (a/0) is not defined if a ≠ 0.
5. ab = 0 iff either a = 0 or b = 0 and both‘a’ and ‘b’ are finite.
In case of limits, it is important to note that the function cannot be manipulated and cancelled as in usual algebra.
For example: (x2-a2)/(x-a) = (x+a)(x-a)/((x-a)) = (x+a)
This can be done in general, but in limits this is not possible until and unless (x-a) ≠ 0 or x ≠ a.
- The limit may exist at a point x = a even if the function is not defined at that point.
- If a function f is defined at a point ‘a’ i.e. f(a) exists even then it is not necessary that the limit at ‘a’ should exist. Moreover, even if the limit exists it need not be equal to f(a).
- Fundamental Results on Limits:
Suppose limx→a f(x) = α and limx→a g(x)=β then we can define the following rules:
- The above rules are applicable only when both the limits i.e. lim f(x) and g(x) exist separately. In addition to above rules, we have two more rules:
ü limx→a kf(x)= k limx→a f(x), where k is a constant
ü limx→a f [g(x)] = f [limx→a g(x)] = f(m), provided f is continuous at g(x) = m. - Some standard limits which should be remembered include:
 Following are some of the frequently used series expansions:
Following are some of the frequently used series expansions:
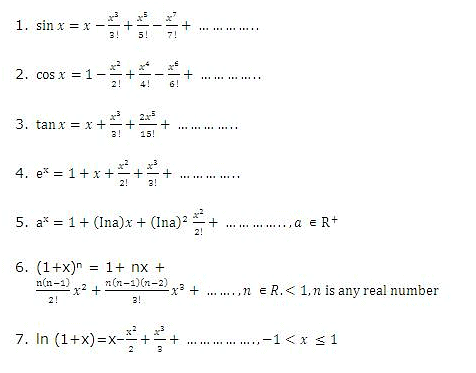
- The term infinite limit means that when x tends to a particular value 'a', then the limit of the function tends to infinity i.e.limx→2 f(x) = ∞.
- In questions which involve the evaluation if limit at infinity, the function f(x) should first be changed to g(1/x) and then we can evaluate the value at ∞.
- If while calculating limits, infinite limit is encountered i.e. a zero is obtained in the denominator as x→a, then there can be two cases:
1. The term (x-a) gets cancelled from the numerator and denominator both.
2. If it does not get cancelled, then the value of the limit is put as infinity.
3. Such limits are termed as improper limits i.e. limx→∞ 1/x2 =∞. - Let f(x), g(x) and h(x) be there real numbers having a common domain D such that h (x) ≤ f(x) ≤ g(x) ∀ x ∈ D. If limx→a h(x) =limx→a g(x)= l, then limx→a f(x) = l. This is known as Sandwich Theorem.
- Let f(x) and g(x) be functions differentiable in the neighbourhood of the point a, except may be at the point a itself. If limx→a f(x) = 0 = limx→a g(x) or limx→af(x)= ∞ = limx→ag(x), then
limx→a f(x)/g(x) = limx→a f' (x)/g(x) = limx→a f' (x)/g'(x) provided that the limit on the right either exists as a finite number or is ± ∞ .
The concept of limits and continuity is quite interrelated. Limits form the base for continuity.
The document Limits Class 11 Notes Maths is a part of the JEE Course Mock Tests for JEE Main and Advanced 2025.
All you need of JEE at this link: JEE
|
357 docs|148 tests
|
FAQs on Limits Class 11 Notes Maths
| 1. What is the definition of a limit in mathematics? |  |
Ans. In mathematics, a limit is a fundamental concept used to describe the behavior of a function as the input values approach a certain value, often denoted as x approaches a specific number or infinity. It represents the value that a function is approaching, but not necessarily reaching, as the input approaches a particular point.
| 2. How is the concept of a limit used in calculus? |  |
Ans. The concept of a limit is central to calculus as it allows us to analyze the behavior of functions and study their properties. Limits are used to calculate derivatives, determine continuity, evaluate integrals, and solve various mathematical problems related to rates of change, slopes, and areas under curves.
| 3. What are the different types of limits? |  |
Ans. There are several types of limits in mathematics, including finite limits, infinite limits, left-hand limits, right-hand limits, and one-sided limits. Finite limits refer to the value that a function approaches as the input approaches a specific number. Infinite limits occur when the function approaches positive or negative infinity. Left-hand limits and right-hand limits describe the behavior of the function as the input approaches a specific value from the left or right side, respectively. One-sided limits exist when the function only approaches a certain value from one direction.
| 4. How do you determine the limit of a function algebraically? |  |
Ans. To determine the limit of a function algebraically, you can analyze the behavior of the function as the input approaches the specified value. This can be done by simplifying the function, factoring, rationalizing, or using algebraic manipulation techniques. You may also apply limit laws, such as the sum, product, quotient, and power laws, to evaluate the limit. If direct substitution leads to an indeterminate form, you may need to use additional techniques like L'Hôpital's rule or trigonometric identities to find the limit.
| 5. Can a function have different limits from the left and right at a specific point? |  |
Ans. Yes, a function can have different limits from the left and right at a specific point. This situation occurs when the function approaches different values as the input approaches the point from the left and right sides. In such cases, the function does not have a limit at that point, as the left-hand limit and the right-hand limit do not coincide. This violates the condition for the existence of a limit, which requires the function to approach the same value from all directions.

|
Explore Courses for JEE exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
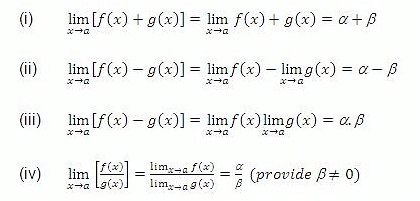
 Following are some of the frequently used series expansions:
Following are some of the frequently used series expansions:

















