Linear Dependence - Vector Algebra, CSIR-NET Mathematical Sciences | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET PDF Download
| Table of contents |

|
| Linear Dependence and Independence |

|
| Basis and Dimension |

|
| Properties on a Linearly Independent and Dependent Basis |

|
| Solved Examples |

|
Linear Dependence and Independence
Linear Dependence
- Let V be a vector space over F. A subset S of V is said to be dependent if there exists distinct vectors a1, a2,......,an in S and scalar c1, c2,.....,cn in F, not all of which are 0, such that c1a1 + c2a2 + ------- + cnan = 0
- If the set S contains finitely many vectors x1, x2,.........,xn then sometimes we can say that the vectors x1, x2,.........,xn are dependent.
- In other words if x1, x2,.........,xn are linearly dependent. Then ∃c1, c2,.........,cn not all zero such that c1x1 + c2x2 + ------- + cnan = 0
- Without loss of generality we can assume c1 ≠ 0 then x1 = (-c1-1 c2)x2 + (-c1-1 c3)x3 + .... + (-c1-1 cn)xn,
hence we can say x1 is linear combinations of the others.
Linear Independent
- Any set containing the vectors x1, x2, ....... , xn defined over a field F is said to be linearly independent if it is not linear dependent i.e. if c1x1 + c2x2 + ......... + cnxn = 0 Implies ci = 0 for all i.
- Example: In ℝ3 the vectors x1 = (3,0,-3), x2 = (-1,1,2), x3 = (4,2,-2), x4 = (2,1,1) are linearly dependent since 2 x1 + x2 - x3 + 0 x4 = 0
Did You Know
1. Vector Space Spanned by Subset: V(F), be a Vector Space and S ⊆ V then V is called spanned by S if L(S) = V.
2. Finitely Generated Vector Space (FGVS) and Non-Finitely Generated Vector Space (NFGVS): A Vector Space V(F), is called finitely generated vector space if there exists finite S ⊆ V such that L(S) = V otherwise non-finitely Generated Vector Space (NFGVS).
Example: V = ℝ³ is vector space over ℝ is finitely generated vector space.
As S = {(1,0,0), (0,1,0), (0,0,1)} ⊆ ℝ³ spanned V = ℝ³.
- ℝ(Q) is non-finitely generated vector space (NFGVS)
- V = ℝ[x] is polynomial space over field ℝ is non-finitely generated vector space (NFGVS)
- V = {f : ℝ → ℝ | f is function } then V is vector space over field ℝ.
Under addition of functions and scalar multiplication to the functions.
V(ℝ) is non-finitely generated vector space (NFGVS)
Basis and Dimension
- Let V be a Vector Space, a basis for V is a linearly independent set of vectors in V which spans the space V .
- The space V is finite-dimensional if it has a finite basis i.e. the basis has finite number of elements. i.e., let V . ⊂ V (F), then S is a basis if
- S is linearly independent
- L(S) = V (F)
Dimension of Vector Space: Dimension of a finite-dimensional vector space is the number of vectors in any basis set of the vector space and it is denoted by dim(V)
Example:
- ℂ(ℂ) is a vector space of dimension one as S = {1} is Linearly independent set which spans C(C)
- ℂ(ℝ) is a vector space of dimension two as S = {1, i} is linearly independent set which spans C(ℝ)
- V = ℝ[x] is polynomial space over field ℝ is infinite dimension vector space.
- V = {f : ℝ → ℝ | f is function } then V is vector space over field ℝ . Under addition of functions and scalar multiplication to the functions. V(ℝ) is infinite dimension vector space.
Ordered Basis:
- If V is a finite-dimensional vector space, then an ordered basis for V is a finite sequence of vectors that is linearly independent and spans V.
- i.e. let S = {x1, x2, ........, xn } be a basis of V (F) then it is called an ordered basis if the position of vectors in S is fixed i.e. the set S is ordered, hence if S = {x1, x2, x3} is an ordered basis then the basis {x2, x1, x3} is considered as different ordered basis.
 |
Download the notes
Linear Dependence - Vector Algebra, CSIR-NET Mathematical Sciences
|
Download as PDF |
Properties on a Linearly Independent and Dependent Basis
- Every subset of a linearly independent set is linearly independent. That is, let V(F) be a vector space, and let S1 ⊆ S2 ⊆ V. If S2 is linearly independent, then S1 is linearly independent
- The empty set is linearly independent; hence every linearly dependent set must be nonempty.
- A set consisting of a single nonzero vector is linearly independent. For if {u} is linearly dependent, then au = 0 for some nonzero scalar a
- A set is linearly independent if and only if the only representations of 0 as linear combinations of its vectors are trivial representations
- A set linearly dependent if and only if the only representations of 0 as linear combinations of its vectors are non-trivial representations
- Any set containing 0 is linearly dependent.
- Let V be a vector space, and let S1 ⊆ S2 ⊆ V. If S1 is linearly dependent, then S2 is linearly dependent
- Let S be a linearly independent subset of a vector space and let v be a vector in V that is not in S. Then S∪{v} is linearly dependent if and only if v ∈ span(S)
- Let u and v be distinct vectors in vector space V, then {u,v} is linearly dependent if and only if u or v is a multiple of the other
- Let V be a vector space over a field of characteristic not equal to two.
a. Let u and v be distinct vectors in V then {u,v} is linearly independent if and only if {u+v,u-v} is linearly independent.
b. Let u,v and w be distinct vectors in V. Then {u,v,w} is linearly independent if and only if {u+v, u+w, v+w} is linearly independent - Let S={u1,u2,...,un} be a finite set of vectors. Then S is linearly dependent if and only if ui=0 or ui ∈ span({u1,u2,...,uk}) for some k(1≤k<n)
- A set S of vectors is linearly independent if and only if each finite subset of S is linearly independent
- If S be a set of nonzero polynomials in P(F) such that the same degree, then S is linearly independent
- If {A₁, A₂, ..., Aₖ} is a linearly independent subset of Mₙₓₙ(F), then {A₁ᵀ, A₂ᵀ, ..., Aₖᵀ} is also linearly independent
- Let f, g ∈ F(R, R) be the functions defined by f(t) = eʳᵗ and g(t) = eˢᵗ where r ≠ s Then f and g are linearly independent in F(R, R)
- Let V be a vector space and β = {u₁, u₂, ..., uₙ} be a subset of V. Then β is a basis for V. If and only if each v ∈ V can be uniquely expressed as a linear combination of vectors of β, that is, can be expressed in the form v = a₁u₁ + a₂u₂ + ... + aₙuₙ
- If a vector space V is generated by a finite set S, then some subset of S is a basis for V, i.e. V has a finite basis
- A vector space V over a field K is said to be finite dimensional if there are a finite number of elements x₁, ..., xₙ in V such that V = ⟨x₁, ..., xₙ⟩. If no such finite number of elements exist in V, V is called infinite dimensional.
- If vector space of continuously differentiable functions is taken then any subset of this vector space is linearly independent if Wronskian of the functions is non-zero.
- Let V be a vector space having a finite basis. Then every basis for V contains the same number of vectors
- Let V be a vector space with dimension n
a. Any finite generating set for V contains at least n vectors, and generating set V that contains exactly n vectors is a basis for V.
b. Any linearly independent subset of V that contains exactly n vectors is a basis for V.
c. Every linearly independent subset of V can be extended to a basis for V. - Let W be a subspace of finite-dimensional vector space V. Then W is finite-dimensional and dim(W) ≤ dim(V). Moreover, if dim(W) = dim(V), then V = W
- If W is a subspace of finite-dimensional vector space V, then any basis for W can be extended to basis for V.
- If W₁ and W₂ are finite-dimensional subspaces of a vector space V, then
a. The subspace W₁ + W₂ is finite-dimensional, and
b. W₁ + W₂ is the smallest subspace of V containing W₁ ∪ W₂ i.e. L(W₁ ∪ W₂) = W₁ + W₂
c. dim(W₁ + W₂) = dim(W₁) + dim(W₂) - dim(W₁ ∩ W₂) - Let W1 and W2 be subspaces of vector space V having dimensions m and n, respectively, where m ≥ n Then
a. dim(W1 ∩ W2) ≤ n
b. dim(W1 + W2) ≤ m + n - Let W1 and W2 be subspaces of a vector space V such that V = W1 ⊕ W2
a. If β1 and β2 are bases for W1 and W2, respectively, then β1 ∩ β2 = φ and β1 ∪ β2 is a basis for V
b. Let β1 and β2 be disjoint bases for subspaces W1 and W2, respectively, of a vector space V if β1 ∪ β2 is a basis for V, then V = W1 ⊕ W2 - Let W be a subspace of a (not necessarily finite-dimensional) vector space V then any basis for W is a subset of basis for V
- Let V be a finite dimensional vector space over field K, and let X and Y be finite subsets of V If Y is linearly independent and V = ⟨X⟩, then |Y| ≤ |X|
- Let V be finite dimensional vector space over field K. If X is a linearly independent subset of V is finite.
- Let V be finite dimensional vector space over K. Then the following statements are equivalent for a subset β of V :
a. β is a basis
b. β is a minimal generating set, that is, no subset of β can generate V
c. β is a maximal linearly independent set - Let V be a vector space of dimension n. Then every linearly independent subset of V with n elements is a basis of V
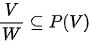 but never contained in V.
but never contained in V.- If xᵢ's are linearly independent in V then it is not necessary that (W + xᵢ)'s are linearly independent
- If xᵢ's are linearly dependent in V then (W + xᵢ)'s are also linearly dependent in V/W.
- For every FDVS V there exists subspaces W₁ and W₂ s.t. V = W₁ ⊕ W₂.
- dim(W₁ ∩ W₂) ≤ min(dim(W₁), dim(W₂))
- dim(W₁ ∩ W₂) ≤ max(0, dim(W₁) + dim(W₂) - dim(V))
- max{dim(W1), dim(W2)} ≤ dim(W1 + W2) ≤ min{dim(W1) + dim(W2), dim(V)}
- If Pn(x, y) denotes vector space of polynomial with degree less than or equal to n in indeterminate x and y then following is true
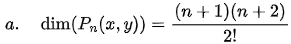
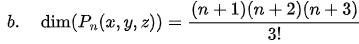 and can be generalized.
and can be generalized.
Solved Examples
Example 1: Are the vectors v1 = (2, 5, 3), v2 = (1, 1, 1), and v3 = (4, −2, 0) linearly independent?
Ans: If none of these vectors can be expressed as a linear combination of the other two, then the vectors are independent; otherwise, they are dependent.
If, for example, v3 were a linear combination of v1 and v2, then there would exist scalars k1 and k2 such that k v + k2 v2b = v3. This equation readswhich is equivalent to
However, this is an inconsistent system.
For instance, subtracting the first equation from the third yields k1 = −4, and substituting this value into either the first or third equation gives k2 = 12.
However, (k1, k2) = (−4, 12) does not satisfy the second equation.
The conclusion is that v3 is not a linear combination of v1 and v2. A similar argument would show that v1 is not a linear combination of v2 and v3 and that v2 is nota linear combination of v1 and v3.
Thus, these three vectors are indeed linearly independent.An alternative—but entirely equivalent and often simpler—definition of linear independence reads as follows.
A collection of vectors v1, v2, …, v r from Rn is linearly independent if the only scalars that satisfy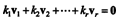
are k1 = k2 = ....= kr = 0.
This is called the trivial linear combination. If, on the other hand, there exists a nontrivial linear combination that gives the zero vector, then the vectors are dependent.
Example 2: Use this second definition to show that the vectors from Example 1— v1 = (2, 5, 3), v2 = (1, 1, 1), and v3 = (4, −2, 0)—are linearly independent
Ans: These vectors are linearly independent if the only scalars that satisfy
are k1 = k2 = k3 = 0. But (*) is equivalent to the homogeneous system
Row‐reducing the coefficient matrix yields
This echelon form of the matrix makes it easy to see that k3 = 0, from which follow k2 = 0 and k1 = 0. Thus, equation (**)—and therefore (*)—is satisfied only by k1 = k2 = k3 = 0, which proves that the given vectors are linearly independent.
Example 3: Are the vectors v1 = (4, 1, −2), v2 = (−3, 0, 1), and v3 (1, −2, 1) linearly independent?
Ans: The equation k1 v1 + k2 v2 + k3 v3 = 0 is equivalent to the homogeneous system
Row‐reduction of the coefficient matrix produces a row of zeros:
Since the general solution will contain a free variable, the homogeneous system (*) has nontrivial solutions. This shows that there exists a nontrivial linear combination of the vectors v1, v2, and v3 that give the zero vector: v1, v2, and v3 are dependent.
Example 4: There is exactly one value of c such that the vectors
are linearly dependent. Find this value of c and determine a nontrivial linear combination of these vectors that equals the zero vector.
Ans: As before, consider the homogeneous system
and perform the following elementary row operations on the coefficient matrix:
In order to obtain nontrivial solutions, there must be at least one row of zeros in this echelon form of the matrix. If c is 0, this condition is satisfied. Since c = 0, the vector v4 equals (1, 1, 1, 0). Now, to find a nontrivial linear combination of the vectors v1, v2, v3, and v4 that gives the zero vector, a particular nontrivial solution to the matrix equation
is needed. From the row operations performed above, this equation is equivalent to
The last row implies that k4 can be taken as a free variable; let k4 = t. The third row then says
The second row implies
and, finally, the first row gives
Thus, the general solution of the homogeneous system (**)—and (*)—is
for any t in R. Choosing t = 1 , for example, gives k1, k2, k3, k4 so
is a linear combination of the vectors v1, v2, v3, and v4 that equals the zero vector. To verify that
simply substitute and simplify:
Infinitely many other nontrivial linear combinations of v1, v2, v3, and v4 that equal the zero vector can be found by simply choosing any other nonzero value of t in (***) and substituting the resulting values of k1, k2, k3, and k4 in the expression k1 v1 + k2 v2 + k3 v3 + k4 v4.
If a collection of vectors from Rn contains more than n vectors, the question of its linear independence is easily answered. If C = { v1, v2, …, vm } is a collection of vectors from Rn and m > n, then C must be linearly dependent. To see why this is so, note that the equation
is equivalent to the matrix equation
Since each vector v j contains n components, this matrix equation describes a system with m unknowns and n equations. Any homogeneous system with more unknowns than equations has nontrivial solutions, a result which applies here since m > n. Because equation (*) has nontrivial solutons, the vectors in C cannot be independent.
|
556 videos|198 docs
|
FAQs on Linear Dependence - Vector Algebra, CSIR-NET Mathematical Sciences - Mathematics for IIT JAM, GATE, CSIR NET, UGC NET
| 1. What is linear dependence in vector algebra? |  |
| 2. How can I determine if a set of vectors is linearly independent? |  |
| 3. What is the significance of linear dependence in the context of CSIR-NET Mathematical Sciences exam? |  |
| 4. Can three vectors in three-dimensional space be linearly dependent? |  |
| 5. What are some examples of linearly dependent vectors? |  |





















