Linear Equations in Two Variables Class 9 Worksheet Maths Chapter 4
Q1. Write each of the following is an equation in two variables:
(i) x = –3
(ii)y = 2
(iii) 2x = 3
(iv) 2y = 5
Sol.
(i)Given equation, x = -3
The above equation can be written in two variables as,
x + 0.y + 3 = 0
(ii) Given equation, y =2
The above equation can be written in two variables as,
0.x + y – 2 = 0
(iii) Given equation, 2x =3
The above equation can be written in two variables as,
2x + 0.y – 3 = 0
(iv) Given equation, 2y =5
The above equation can be written in two variables as,
2y-5= 0
(0)x + 2y- 5= 0
Q2. Write each of the following equations in the form ax + by + c = 0 and also write the values of a, b and c in each case:
(i) 2x + 3y = 3.47
(ii) x – 9 = √3 y
(iii) 4 = 5x – 8y
(iv) y = 2x
Sol.
(i) 2x + 3y – 3.47 = 0; a = 2, b = 3 and c = –3.47
(ii) x – √3y – 9 = 0; a = 1, b = - √3 and c = –9
(iii) –5x + 8y + 4 = 0; a = –5, b = 8 and c = 4
(iv) –2x + y + 0 = 0; a = –2, b = 1 and c = 0
Q3. (a) Is (3, 2) a solution of 2x + 3y = 12?
(b) Is (1, 4) a solution of 2x + 3y = 12?
(c) Is  a solution of 2x + 3y = 12?
a solution of 2x + 3y = 12?
(d) Is 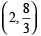 a solution of 2x + 3y = 12?
a solution of 2x + 3y = 12?
Sol.
(a) Yes,
2(3)+ 3(2)= 6+6 =12
(b) No,
2(1)+ 3(4)= 2+12 =14
(c) Yes,
2(-5)+ 3(22/3)= -10+ 22 =12
(d) Yes,
2(2)+ 3(8/3)= 4+8 =12
Q4. Find four different solutions of the equation x + 2y = 6.
Sol. To find four different solutions of the equation x+2y=6, we can choose different values for y and solve for x.
y=0
x+2⋅0=6x=6So, one solution is .
y = 1
x+2⋅1=6x+2=6x=4Another solution is .
y=2
x+2⋅2=6x+4=6x=2Another solution is .
y=3
x+2⋅3=6x+6=6x=0Another solution is
Therefore, the four different solutions of the equation x+2y=6 are (6,0),(4,1),(2,2),(0,3).
Q5. Find two solutions for each of the following equations:
(i) 4x + 3y = 12
(ii) 2x + 5y = 0
(iii) 3y + 4 = 0
Sol.
1) 4x+3y=12for y=44x+12=12 x=0for y=04x+0=12 x=3(0,4) & (3,0) are 2 solution2) 2x+5y=0for y=−22x−10=0 x=5for y=−42x−20=0 x=10(5,−2) and (10,−4) are 2 solutions3) 3y+4=0y=−4/3 is only solution
Q6. Find the value of k such that x = 2 and y = 1 is a solution of the linear equation 2x – ky + 7 = 8
Sol. We can find the value of k by substituting the values of x and y in the given equation.
By substituting the values of x = 2 and y = 1 in the given equation
2x – ky + 7 = 8
⇒ 2(2) – k(1) + 7 = 8
⇒ 4- k+ 7=8
⇒ -k=8-11
k=3
Therefore, the value of k is 3.
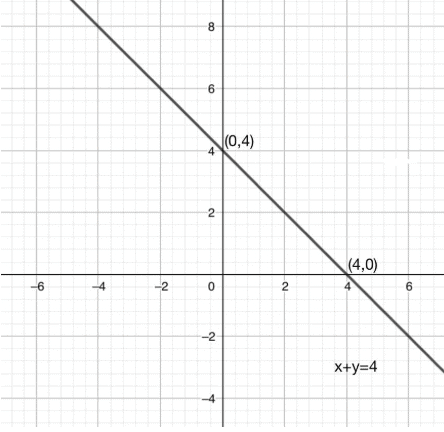
Q7. Draw the graph of y+x = 4.
Sol. Let x be 0 = (0,4)
Let y be 0 = (4,0)
Q8. Force applied on a body is directly proportional to the acceleration produced in the body.
Write an equation to express this situation and plot the graph of the equation.
Sol. Given that, the force (F) is directly proportional to the acceleration (a).
i.e., F∝a
⇒F=ma [where, ,m=arbitrary constant and take value 6 kg of mass ]
∴ F=6a
(i) If a=5m/s2, then from Eq. (i), we get
F=6×5=30N
(ii) If a=6m/s2, then from Eq. (i), we get
F=6×6=36N
Here, we find two points A (5, 30) and B (6, 36). So draw the graph by plotting the points and joining the line AB.
Q9. For each of the graph given in the following figure select the equation whose graph it is from the choices given below: (i) x + y = 0
(i) x + y = 0
(ii) x – y = 0
(iii) 2x = y
(iv) y = 2x + 1
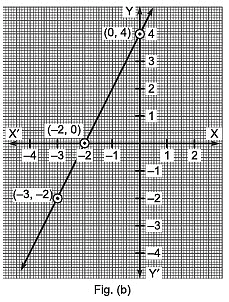 (i) x + y = 0
(i) x + y = 0
(ii) x – y = 0
(iii) y = 2x + 4
(iv) y = x – 4
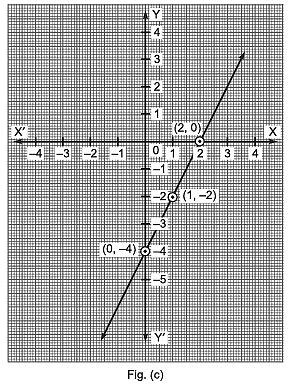
(i) x + y = 0
(ii) x – y = 0
(iii) y = 2x + 1
(iv) y = 2x – 4
 (i) x + y = 0
(i) x + y = 0
(ii) x – y = 0
(iii) 2x + y = –4
(iv) 2x + y = 4
Sol.
(a) x – y = 0
(b) y = 2x + 4
(c) y = 2x – 4
(d) 2x + y = –4
Q10. Which of the following is not a linear equation in two variables?
(i) px + qy + c = 0
(ii) ax2 + bx + c = 0
(iii) 3x + 2y = 5
Sol.
(ii) ax2 + bx + c = 0
(ii) is not a linear equation because it consists x2 in it. Linear equation will not contain any exponent to variables
Q11. One of the solutions of the linear equation 4x – 3y + 6 = 0 is
(i) (3, 2)
(ii) (–3, 2)
(iii) (–3, –2)
Sol. Option (iii) –3, –2
Q12. lx + my + c = 0 is a linear equation in x and y. For which of the following, the ordered pair (p, q) satisfies it:
(i) lp + mq + c = 0
(ii) y = 0
(iii) x + y = 0
(iv) x = y
Sol.
lp+mq+c=0
To check if (p,q) satisfies the equation: l⋅p+m⋅q+c=0
This matches the form of the linear equation lx+my+c=0, so statement (i) is correct.
Q13. What is the equation of the x-axis?
Sol. The x-axis is the horizontal line where y=0.
Equation of the x-axis: y=0.
Q14. What is the equation of the y-axis?
Sol. The y-axis is the vertical line where x=0.
Equation of the y-axis: x=0.
Q15. How many solutions do a linear equation in two variables x and y have?
Sol.
A linear equation in two variables will have infinite solutions
|
40 videos|471 docs|57 tests
|
FAQs on Linear Equations in Two Variables Class 9 Worksheet Maths Chapter 4
| 1. What is the general form of a linear equation in two variables? |  |
| 2. How many solutions can a system of two linear equations in two variables have? |  |
| 3. How do you graph a linear equation in two variables? |  |
| 4. What is the significance of the slope in a linear equation? |  |
| 5. How can you solve a system of linear equations in two variables algebraically? |  |