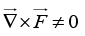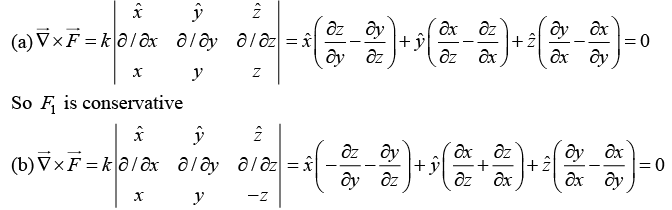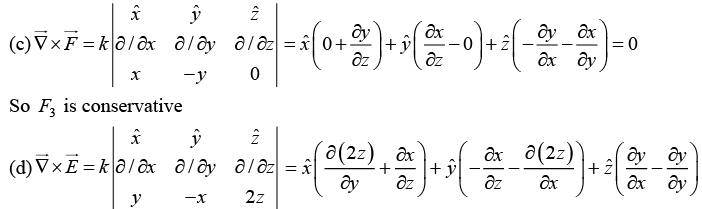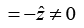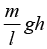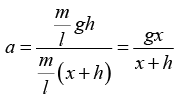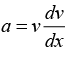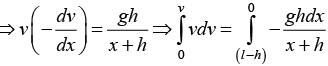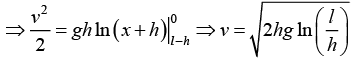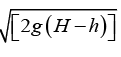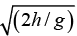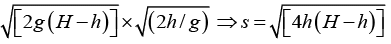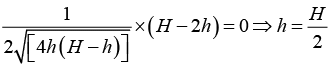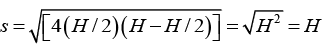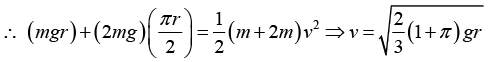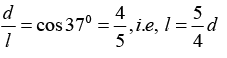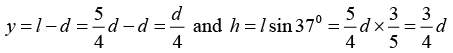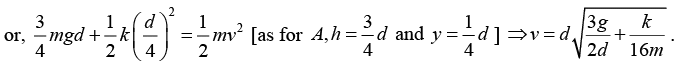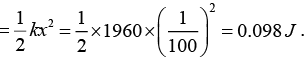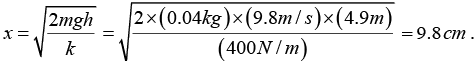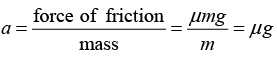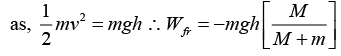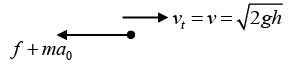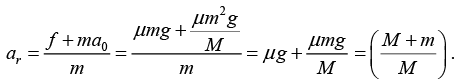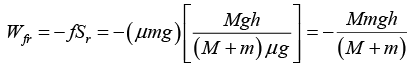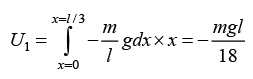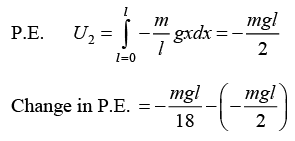Linear Momentum & Energy: Assignment | Mechanics & General Properties of Matter - Physics PDF Download
Q.1. Check whether given forces are conservative or non-conservative force.
(a) 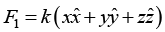
(b) 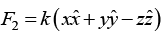
(c) 
(d) 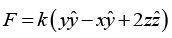
For time varying fields
So F2 is conservative
So F4 is non-conservative
Q.2. A chain of length l (AB) is kept on a smooth table and it’s length h hangs vertically. End A is set free. Find velocity of the end with which it moves on the table.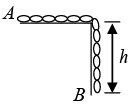
Mass of hanging part
Total mass pulled = m/l(x+h)
Acceleration
As
x is decreasing as v increases.
dv/dx is negative
Q.3. A small disc A slides down with initial velocity equal to zero from the top of a smooth hill of height H having a horizontal portion. What must be the height of the horizontal portion h to ensure the maximum distance s covered by the disc? What is equal to?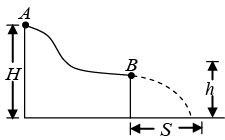
In order to obtain the velocity at point B , we apply the law of conservation of energy
So,
Loss in PE = Gain in KE ⇒ (H -h) = 1/2(H-h) = 1/2 mv2 ⇒ v = mg
Further, h = 1/2gt2 ⇒ t =
Now, s = v x t =
For maximum value of s ds/dh = 0 ⇒
Substituting h = H/2, in equation (i) we get
Q.4. A smooth narrow tube in the form of an arc AB of a circle of centre O and radius r is fixed so that A is vertically above O and OB is horizontal. Particles P of mass m and Q of mass 2m with a light inextensible string of length (πr/2) connecting them are placed inside the tube with P at A and Q at B and released from rest. Assuming the string remains taut during motion, find the speed of particles when P reaches B.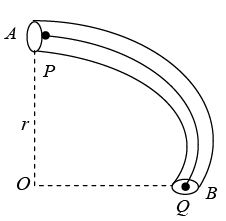
All surface are smooth. Therefore, mechanical energy of the system will remain
conserved,
⇒ Decreases in PE of both the block = increase in KE of both the blocks
Q.5. One end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 370 with the horizontal as shown in figure. When the system is released from rest, find the speed of the ring when the spring becomes horizontal. (sin 370 = 3/5.
If l is the stretched length of the spring, then from figure
So, the stretch
Now, taking point B as reference level and applying law of conservation of mechanical energy between A and B,
EA = EB[as for B, h = 0 and y = 0]
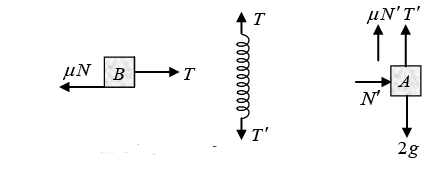
Q.6. Two blocks A and B are connected to each other by a string and a spring. The string passes over a frictionless pulley as shown in figure. Block B slides over the horizontal top surface of a stationary block C and the block A slides along the vertical side of C , both with the same uniform speed. The coefficient of friction between the surfaces of the blocks is 0.2. The force constant of the spring is 1960 Nm-1 . If the mass of block A is 2 kg, calculate the mass of block B and the energy stored in the spring. (g = 9.8 m/s2).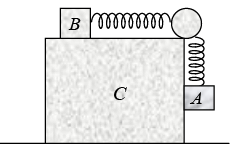
Let m be the mass of B. From its free – body diagram
Where T = tension of the string and N = mg ⇒ T = μmg
From the free - body diagram of the spring ⇒ T -T' = 0
Where T' is the force exerted by A on the spring ⇒ T = T' = μmg
From the free - body diagram A ⇒ 2 g - (T' + μN') = 2 x 0 = 0
Where N' is the normal reaction of the vertical wall of C on A and N' = 2 x 0 (as there is no horizontal acceleration of A)
∴ 2g = T' = μmg or m = 2g/μg = 2/0.2 = 10kg
Tensile force on the spring = T or T' = μmg = 0.2 x 10 x 9.8 = 19.6 N
Now, in a spring tensile force = force constant x extension
19.6 = 1960x ⇒ x = 1/100 m
or, U (energy of a spring)
Q.7. A 0.5 kg block slides from the point A on a horizontal track with an initial speed 3 m/s towards a weightless horizontal spring of length 1 m and force constant 2 N/m. The part AB of the track is frictionless and the part BC has the coefficient of static and kinetic friction as 0.22 and 0.20 respectively. If the distance AB and BD are 2m and 2.14 m respectively, find the total distance through which the block moves before it comes to rest completely. (g = 10m/s2)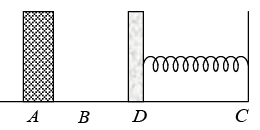
As the track AB is frictionless, the block moves this distance without loss in its initial.
KE = 1/2 mv2 x 0.5 x 32 = 2.25 J. In the path BD as friction is present, so work doneagainst friction
= μkmgs = 0.2 x 0.5 x 10 x 2.14 = 2.14 J
So, at D the KE of the block is = 2.25 - 2.14 = 0.11 J
Now, if the spring is compressed by
0.11 = 1/2 x h x x2 + μkmgx ⇒ 0.11 = 1/2 x x2 + 0.2 x 0.5 x 10x ⇒ x2 + x - 0.11 = 0
which on solving gives positive value of x = 0.1m
After moving the distance x = 0.1m the block comes to rest. Now the compressed springexerts a force:
F = kx = 2 x 0.1 = 0.2N
On the block whole limiting frictional force between block and track is fL = μsmg
= 0.22 x 0.5 x 10 = 1.1 N. Since, F < fL. The block will not move back. So, the total distance moved by the block = AB + BD + 0.1 = 2 + 2.14 + 0.1 = 4.24 m
Q.8. A particle is placed at the point A of a frictionless track ABC as shown in figure. It is pushed slightly towards right. Find its speed when it reaches the point B. Take g = 10 m/s2.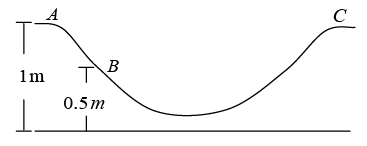
Let us take the gravitational potential energy to be zero at the horizontal surface shown in the figure. The potential energies of the particle at A and B are.
UA = Mg (1m) and UB = Mg(0.5).
The kinetic energy at the point A is zero. As the track is frictionless, no energy is lost. The normal force on the particle does no work. Applying the principle of conservation of energy,
UA + KA = UB + KB ⇒ Mg(1m) = Mg(0.5m) + 1/2 Mv2B
or, 1/2 v2b = g(1m - 05m) = (10m/s2) x 0.5 m = 5m2/s2 ⇒ vB = √10m/s
Q.9. Figure shows a smooth curved track terminating in a smooth horizontal part. A spring of spring constant 400 N/m is attached at one end to a wedge fixed rigidly with the horizontal part. A 40 g mass is released from rest at a height of 4 × 9 m on the curved track. Find the maximum compression of the spring.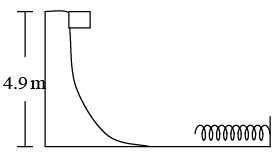
At the instant of maximum compression the speed of the 40 g mass reduces to zero. Taking the gravitational potential energy to be zero at the horizontal part, the conservation of energy shows, ⇒ mgh = 1/2 kx2
where m = 0.04kg, h = 4.9m, k = 400 N/m and x is the maximum compression.
Thus,
Q.10. A particle slides along a track with elevated ends and a flat central part as shown in figure. The flat portion BC has a length l = 3.0m. The curved portions of the track are frictionless. For the flat part the coefficient of kinetic friction is μk = 0.20, the particle is released at point A which is at height h = 1.5m above the flat part of the track. Where does the particle finally comes to rest?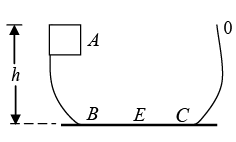
As initial mechanical energy of the particle is mgh and final is zero,, so loss in mechanical energy = mgh. This mechanical energy is lost in doing work against friction
in the flat part, So, loss in mechanical energy = work done against friction
or, mgh = μmgs ⇒ s = h/μ = 1.5/0.2 = 7.5m
After starting from B the particle will reach C and then will rise up till the remaining KE at C is converted into potential energy. It will then again descend ant at C will have the same value as it had when ascending, but now it will move from C to B . The same will be repeated and finally the particle will come to rest at E such that
BC + CB + BE = 7.5 ⇒ 3 + 3 + BE = 7.5 ⇒ BE = 1.5
So, the particle comes to rest at the centre of the flat part.
Q.11. A small body of mass m is located on a horizontal plane at the point O. The body acquires a horizontal velocity v0 due to friction. Find, the mean power developed by the friction force during the motion of the body, if the frictional coefficient
μ = 0.27, m = 1.0 kg and v0 = 1.5 m/s.
The body gains velocity due to friction. The acceleration due to friction.
Further, v0 = αt ⇒ V0/α = V0/μg (i)
From work energy theorem,
Work done by force of friction = change in kinetic energy
or w = 1/2 mv02 (ii)
Mean power = W/t
From equation (i) and (ii)
Pmain = 1/2 μmgv0 ⇒ Pmean = 1/2 x 0.27 x 1.0 x 9.8 x 1.5 = 2.0
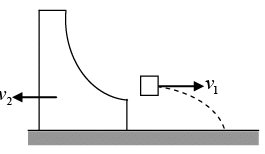
Q.12. A small disc of mass m slides down a smooth hill of height h without initial velocity and gets onto a plank of mass M lying on a smooth horizontal plane at the base of hill figure. Due to friction between the disc and the plank, disc slows down and finally moves as one piece with the plank.
(a) Find out total work performed by the friction forces in this process.
(b) Can it be stated that the result obtained does not depend on the choice of the reference frame.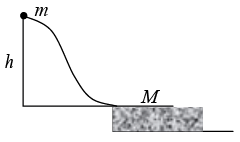
(a) When the disc slides down and comes onto the plank, then
(i)
Let v1 be the common velocity of the disc and plank when they move together. From law of conservation of linear momentum,(ii)
Now, change in KE = (K)f - (K)i = (work done)friction
(b) In part (a) we have calculated work done from the ground frame of reference. Now, let us take plank as the reference frame.
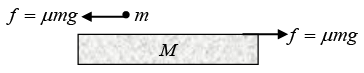
Acceleration of plank α0 = f/M = μmg/M
Free body diagram of disc with respect to plank is shown in figure.
Here, ma0 = pseudo force
∴ Retardation of disc w.r.t. plank.
The disc will stop after traveling a distance Sr relative to plank, where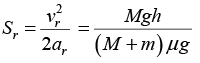
∴ work done by friction in this frame of reference
Note: Work done by friction in this problem does not depend upon the frame of reference, general work depends upon reference frame.
Q.13. The displacement x of a particle moving in one dimension, under the action of a constant force is related to time t by the equation t = √x + 3 where x is in metre and t in second.
Calculate: (a) the displacement of the particle when its velocity is zero,
(b) the work done by the force in the first 6 s.
As t = √x + 3 i.e, x = (t - 3)2 (i)
So, v = (dx/dt) = 2 (t - 3) (ii)
(a) v will be zero when 2 (t - 3) = 0 i.e, t = 3.
Substituting this value of t in equation (i)
x = (3 - 3)2 = 0 , i.e., when velocity is zero, displacement is also zero.
(b) From equation (ii),
(v) t = 0 = 2(0-3) = -6m/s and (v)t = 6 = 2(6-3) = -6m/s
So, from work – energy theorem
W = ΔkE = 1/2 Mi.e., work done by the force in the first 6s is zero.
Q.14. A small cube of mass m slides down a circular path of radius R cut into a large block of mass M, as shown in figure. M rests on a table, and both blocks move without friction. The block are initially at rest, and m starts from the top of path. Find the horizontal distance from the bottom of block when cube hits the table.
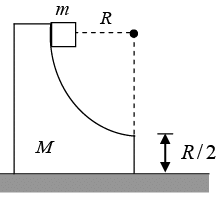
mv1 = Mv2 (i)
(ii)
(iii)
The desired distance is S = (v1+ v2)t (iv)
Solving equations (i) and (ii) for v1 and v2 and substituting in equation (iv) we get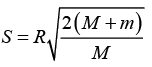
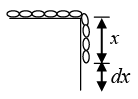
Q.15. A chain of length l has 1/3rd of mass m hanging on a smooth table. Find K.E. of the chain as it slips off completely.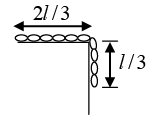
Mass of small element of length dx of chain dm = m/l x dx
Taking horizontal surface as datum,
P.E. of overhanging partg x dx x x
Here, x is the length of the hanging part
Total P.E.
When whole chain slips off the table,
K.E. of chain = ΔU = 4mgl/9 = (No loss in friction)
|
61 videos|23 docs|25 tests
|
FAQs on Linear Momentum & Energy: Assignment - Mechanics & General Properties of Matter - Physics
| 1. What is linear momentum and how is it related to energy? |  |
| 2. How is linear momentum conserved in a collision? |  |
| 3. What is the difference between elastic and inelastic collisions in terms of linear momentum and energy? |  |
| 4. How does the conservation of linear momentum apply to explosions? |  |
| 5. How is linear momentum related to the concept of impulse? |  |