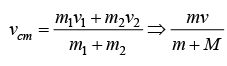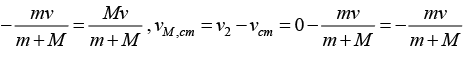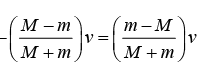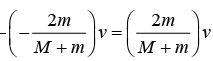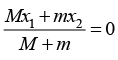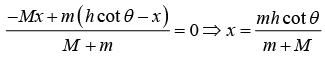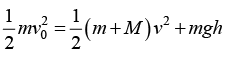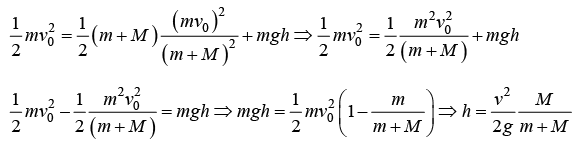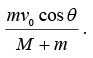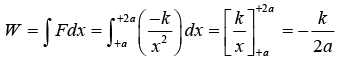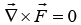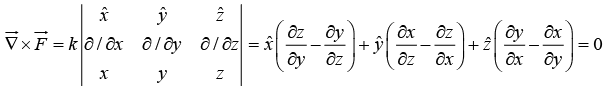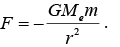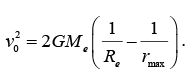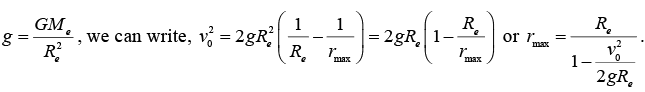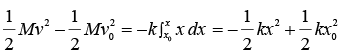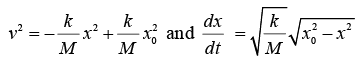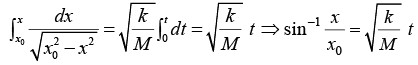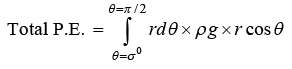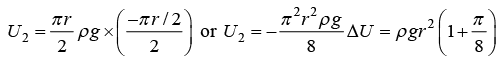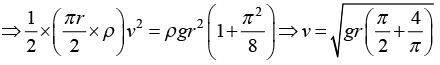Linear Momentum & Energy | Mechanics & General Properties of Matter - Physics PDF Download
| Table of contents |

|
| Linear Momentum |

|
| Conservation of Momentum |

|
| Energy |

|
| Gravitation |

|
| Spring Force |

|
Linear Momentum
In Newtonian mechanics, linear momentum, translational momentum, or simply momentum is the product of the mass m and velocity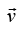 of an object.
of an object.
It is a vector quantity, possessing a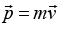
In SI units, momentum is measured in kilogram-meter per second (kg-m/s).
Conservation of Momentum
In the last section we found that the total external force F acting on a system is related to the total momentum P of the system by 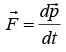
Consider the implications of this for an isolated system, that is, a system which does not interact with its surroundings. In this case 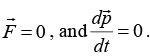 The total momentum is constant; no matter how strong the interactions among an isolated system of particles, and no matter how complicated the motions, the total momentum of an isolated system are constant. This is the law of conservation of momentum. If external force is zero then momentum of system is conserve and center of mass of system is not changing.
The total momentum is constant; no matter how strong the interactions among an isolated system of particles, and no matter how complicated the motions, the total momentum of an isolated system are constant. This is the law of conservation of momentum. If external force is zero then momentum of system is conserve and center of mass of system is not changing.
The Center of Mass Frame
Consider a inertial frame S and another inertial frame S' that at constant velocity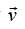 with respect to S .system of particle is moving with respect to S' is
with respect to S .system of particle is moving with respect to S' is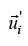 . Same system of particles have velocity with respect to S is
. Same system of particles have velocity with respect to S is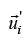
From Galilean transformation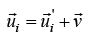
Let us consider the unique frame in which the total momentum of a particles is zero. This is called the center of mass frame or C .M frame If Total momentum from is 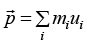 from S frame then the center of mass is S ' that moves with velocity
from S frame then the center of mass is S ' that moves with velocity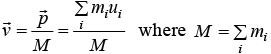 is total mass
is total mass
So from S ' or center of mass frame the momentum is
So center of mass frame is known as zero momentum frame.
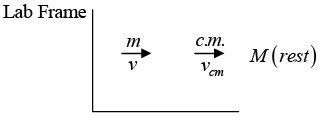
Example 1: A mass m with speed v approaches a stationary particle of mass M
(a) Find the velocity of center of mass with respect to laboratory
(b) Find the velocity of particle with respect to center of mass before collision.
(c) Find the velocity of particles after collision such that center of mass has zero momentum i.e. with respect to center of mass.
(d) Find the velocity of particles just after collision with respect to laboratory.
(a) m1 = m m2 = M v1 = v and v1 = 0
(b) Vm,cm = v1 - vcm = v
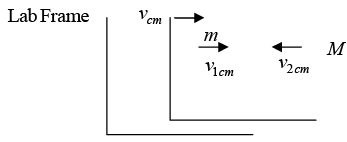
(c) If momentum of center of mass is zero then velocity of mass m with respect to center of mass is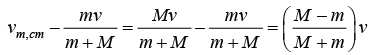
If momentum of center of mass is zero then velocity of mass M with respect to center of mass is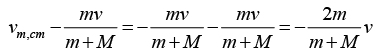
(d) Then velocity of particle m after collision with respect
Then velocity of particle m after collision with respect
Example 2: A block of mass m slides down frictionless wedge of mass M, when block will reach the bottom how much horizontal distance wedge will move.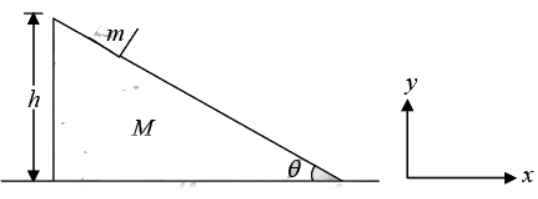
Since there is not any force in horizontal direction, then momentum in horizontal direction is conserved. Therefore, center of mass in horizontal distance will not change. x distance of mass M move towards left with respect to surface. Same time m will move h cot θ - x with respect to surface towards right.
Let us assume center of mass is at origin so
put x1 = -x, x2 = h cot θ - x so
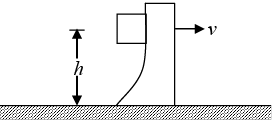
Example 3: All the surface shown in figure are smooth wedge of mass M is free to move .Block of mass m is given a horizontal velocity v0 as shown in figure. Find the maximum height h attained by m.
Since there is not any force in horizontal direction so momentum in horizontal direction is conserved.
From conservation of momentum mv0 = (m + M) v ⇒ v = mv0/m +M
From conservation of energy
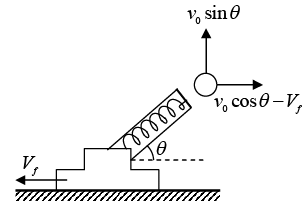
Example 4: A loaded spring gun, initially at rest on a horizontal frictionless surface, fires a marble at angle of elevation θ. The mass of the gun is M, the mass of the marble is m and the muzzle velocity of the marble is v0. What is the final motion of the gun?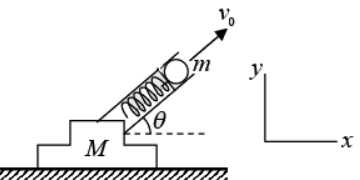
Take the physical system to be the gun and marble, Gravity and the normal force of the table act on the system. Both these forces are vertical. Since, there are no horizontal external forces.
The x component of the vector equation F = dP/dt is
0 = dpx/dt (1)
According to equation (1) Px is conserved:
Px,initial = Px,final (2)
Let the initial time be prior to firing the gun. Then Px,initial = 0. Since the system is initially at rest. After the marble has left the muzzle, the gun recoils with some speed Vf, and its final horizontal momentum is MVf, to the left. Finding the final velocity of the marble in volves a subtle point, however. Physically, the marble’s acceleration is due to the force of the gun, and the gun’s recoil is due t the reaction force of the marble. The gun stops accelerating once the marble leaves the barrel, so that at the instant the marble and the gun part company, the gun has its final speed Vf. At that same instant the speed of the marble relative to the gun is v0. Hence, the final horizontal speed of the marble relative to the table is v0 cos θ - Vf. By conservation of horizontal momentum. We have, 0 = m (v0cos θ) - mVf - MVf ⇒ vf =
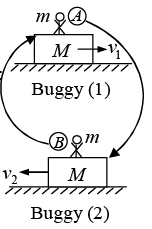
Example 5: Two identical buggies 1 and 2 with one man in each, move without friction due to inertia along the parallel rails towards each other. When the buggies get opposite to each other, the men exchange their places by jumping in the direction perpendicular to the motion direction. As a consequence, buggy 1 stops and buggy 2 keeps moving in the same direction, with its velocity becoming equal to v. Find the initial velocities of the buggies v1 and v2 if the mass of each buggy (without a man) equals M and the mass of each man is m.
(i) Initial condition of the buggies:
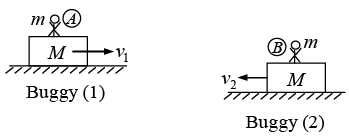
(ii) Status of buggies during jump:
(iii) Status of buggies after jump
During this exchange momentum will be conserved because there is no force is horizontal direction. Conservation of momentum for buggy (1) Mv1 - mv2 = 0 …(i)
Conservation of momentum for buggy (2) Mv2 - mv1 = (m + M)v …(ii)
From (i) and (ii)
But in term of vector: v2 has opposite direction as v1.
Then
Energy
In Physics, Energy is the quantitative property that must be transferred to an object in order to perform work on, or to transfer heat to the object Energy is a conserved quantity; the law of conservation of energy states that energy can be converted in form, but not created or destroyed. The SI unit of energy is the joule, which is the energy transferred to an object by the work of moving it a distance of 1 metre against a force of 1 Newton.
Conservation of Energy: The energy can neither will created nor destroy, it can be transform from one form to another.
Different Form of Energy used in Mechanics
Kinetic energy
The energy which is responsible for motion of the particle. If particle of mass m moving with velocity 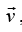 then kinetic energy is given by
then kinetic energy is given by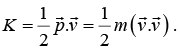
Kinetic energy in Cartesian coordinate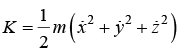
Kinetic energy in cylindrical coordinate 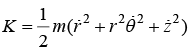
Kinetic energy in spherical coordinate 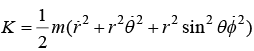
Work Done by Force Work done by the constant force is given as W =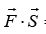 = FS cosθ, where force
= FS cosθ, where force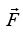 is force and making θ angle with displacement vector
is force and making θ angle with displacement vector 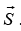 In general work done is a area under the force F and displacement S, which is for the variable force is defined as W =
In general work done is a area under the force F and displacement S, which is for the variable force is defined as W =
Work Done by a Variable Force
So far we have considered the work done by a force which is constant both in magnitude and direction. Let us now consider a force which acts always in one direction but whose magnitude may keep on varying. We can choose the direction of the force as x - axis. Further, let us assume that the magnitude of the force is also a function of x or say F(x) is known to us. Now we are interested in finding the work done by this force in moving a body from x1 to x2.
Work done in a small displacement from x and x + dx will be
dW = F.dx
Now, the total work can be obtained by integration of the above elemental work from x1 to x2 or  It is important to note that
It is important to note that is also the area under F -x graph between x = x1 to x = x2.
is also the area under F -x graph between x = x1 to x = x2.
Potential energy (U)
The energy which is required to perform the work is known as potential energy U. Hence force is defined as F = -(∂U/∂r. Then potential energy Ub - Uα = 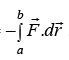 For the conservative force one can say potential energy is negative integral of the force .one can say in another way change in potential energy with respect to position is cause of force F.
For the conservative force one can say potential energy is negative integral of the force .one can say in another way change in potential energy with respect to position is cause of force F.
There is different type of potential energy. For example, electrostatic potential energy, gravitation potential energy, stored energy in spring, mass energy in relativistic mechanics.
Total energy E is sum of kinetic energy K and potential energy U. So total energy E = K + U
Conservative and Non Conservative Force
Field We considered the forces which were although variable but always directed in one dimension. However, the most general expression for work done is
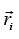 = initial position vector and
= initial position vector and 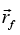 = final position vector
= final position vector
A conservative force is a force with the property that the total work done in moving a particle between two points is independent of the taken path. Equivalently, if a particle travels in a closed loop, the total work done (the sum of the force acting along the path multiplied by the displacement) by a conservative force is zero.
For example Gravitational force is an example of a conservative force, while frictional force is an example of a non-conservative force.
Mathematical Interpretation of Conservative Force
A Force field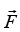 defined everywhere in space (or within a simply connected volume of space), is called a conservative force or conservative if it meets any of these three equivalent conditions:
defined everywhere in space (or within a simply connected volume of space), is called a conservative force or conservative if it meets any of these three equivalent conditions:
(1) The curl of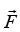 is the zero vector:
is the zero vector: 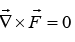
(2) There is zero net work (W) done by the force when moving a particle through a trajectory that starts and ends in the same place 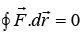
(3) The force can be written as the negative gradient of a potential,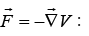
Example 6: A body is displaced from A = ( 2m, 4 m, -6 m) to 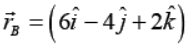 m under a constant force
m under a constant force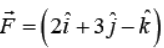 N. Find the work done.
N. Find the work done.
Example 7: A force F = - k/x2 (x ≠ 0) acts on a particle in x - direction. Find the work done by this force in displacing the particle from x = + α to x = +2a . Here, k is a positive constant.
Work done by area under F - S or F - x Graph
Example 8: The field is given as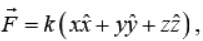 where k is positive constant, then check whether the field is conservative or non conservative.
where k is positive constant, then check whether the field is conservative or non conservative.
For conservative field
which justify the following force is conservative in nature.
Work Energy Theorem
The kinetic energy of a particle of mass m, moving with a speed v, is defined as T = 1/2 mv2. Let us consider a particle that moves from point 1 to point 2 under the action of a force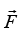 . The total work done on the particle by the force as the particle moves from 1 to 2 is, by definition, the line integral
. The total work done on the particle by the force as the particle moves from 1 to 2 is, by definition, the line integral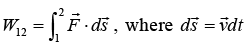 is the displacement vector along the particle’s trajectory. If the particle under-goes an infinitesimal displacement
is the displacement vector along the particle’s trajectory. If the particle under-goes an infinitesimal displacement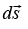 under the action of force
under the action of force , the scalar product dW =
, the scalar product dW = is the infinitesimal work done by the force
is the infinitesimal work done by the force as the particle undergoes the displacement
as the particle undergoes the displacement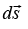 along the particle’s trajectory. We use the Newton’s second law of motion,
along the particle’s trajectory. We use the Newton’s second law of motion,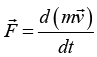 in the equation to obtain an expression for the infinitesimal work
in the equation to obtain an expression for the infinitesimal work
The scalar quantity 1/2 mv2 is the kinetic energy of the particle, it follows that dW = dT . This Equation dW = dT in the differential form of the work-energy theorem. It states that the differential work of the resultant of forces acting on a particle is equal, at any time, to the differential change in the kinetic energy of the particle. Integrating equation between point 1 and point 2, corresponding to the velocities
v1 and v2 of the particle, we get W12 = 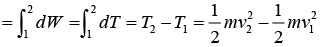
This is the work-energy theorem, which states that the work done by the resultant force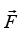 acting on a particle as it move from point 1 to point 2 along its trajectory is equal to the change in the kinetic energy (T2 - T1) of the particle during the given displacement. When the body is accelerated by the resultant force, the work done on the body can be considered a transfer of energy to the body, where it is stored as kinetic energy.
acting on a particle as it move from point 1 to point 2 along its trajectory is equal to the change in the kinetic energy (T2 - T1) of the particle during the given displacement. When the body is accelerated by the resultant force, the work done on the body can be considered a transfer of energy to the body, where it is stored as kinetic energy.
Energy Conservation Theorem
If there exists a scalar function ∅(x,y,z,t), so that we could write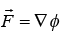 . We shall say that the vector field
. We shall say that the vector field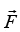 is a potential field. The scalar function ∅(x,y,z,t), is then called the potential function of the field. The vector field
is a potential field. The scalar function ∅(x,y,z,t), is then called the potential function of the field. The vector field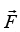 is called conservative if ∅ does not explicitly depend on time. The potential function ∅(x,y,z,t), in this case, is called the force potential.
is called conservative if ∅ does not explicitly depend on time. The potential function ∅(x,y,z,t), in this case, is called the force potential.
It is easy to show that if the force field is conservative the work done in moving the particle from 1 to 2 is independent of the path connecting 1 and 2 . The total work done on the particle by the force 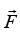 as it moves from 1 to 2 is given by
as it moves from 1 to 2 is given by 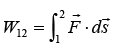
For a conservative force filed 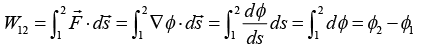
Thus, the total work done is equal to the difference in force potential no matter how the particle moves from 1 to 2 following differential relation dW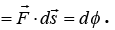
If we now write θ(x,y, z) = -U (x,y, z) (inserting a minus sign for reasons of convention) and express the force as 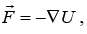 then the scalar function U is called the potential energy of the particle.
then the scalar function U is called the potential energy of the particle.
When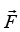 is expressed as in the above equation, the work done becomes W12 = U1-U2 It may be noted that the line integral of the field
is expressed as in the above equation, the work done becomes W12 = U1-U2 It may be noted that the line integral of the field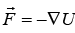 along a closed curve (called circulation) is zero as shown below
along a closed curve (called circulation) is zero as shown below 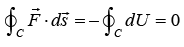
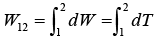 it can be concluded that T1 + U1 = T2 + U2.
it can be concluded that T1 + U1 = T2 + U2.
It says that the quantity T + U remains a constant as the particle moves from point 1 to point 2. Since 1 and 2 are arbitrary points, we have obtained the statement of conservation of total mechanical energy E = T+ U = constant.
Thus, the energy conservation theorem states that the total energy of a particle in a conservative force field is constant. It is instructive to note that equation (6) does not uniquely determine the function ∅. We could as well define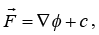 where c is any constant. Hence, the choice for the zero level of ∅, and consequently U, is arbitrary.
where c is any constant. Hence, the choice for the zero level of ∅, and consequently U, is arbitrary.
We can verify directly from equation (11) that the total energy in a conservative field is a constant of the motion.
We have 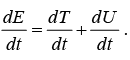
The kinetic energy term can be written as 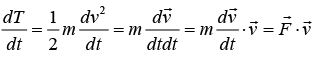
The potential energy U depends on time only through the changing position of the particle: U = U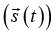 = U (x (t), y (t), z (t)). Thus, we have
= U (x (t), y (t), z (t)). Thus, we have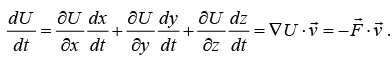 If follows that dE/dt =
If follows that dE/dt =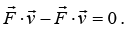
Thus, the total energy of the particle moving in a conservative force field is a constant during the motion.
Gravitation
Force Let us consider a conservative force then we have
then we have 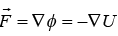
Therefore, we have the following relations: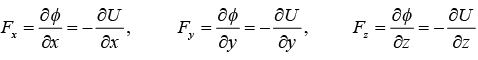
This shows that the partial derivative of force potential in a given direction gives the force in that direction. An example of a force that derives from a potential is gravitational force 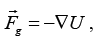

where the gravitational acceleration vector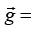 (gx, gy, gz). It follows that the negative of partial derivative of potential energy in a given direction gives the gravitational force in that direction. If gravitational acceleration vector is given by
(gx, gy, gz). It follows that the negative of partial derivative of potential energy in a given direction gives the gravitational force in that direction. If gravitational acceleration vector is given by 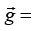 g(0, 0,-1)
g(0, 0,-1)
then we have 
Integrating the last of the above equation to obtain U = mgz + f(x, y) Setting f(x, y) = 0, the potential energy of the particle in a gravitational field is given by U = mgz where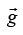 acts in the negative z direction. The total mechanical energy E is conserved when a particle moves under the action of the gravitational field.
acts in the negative z direction. The total mechanical energy E is conserved when a particle moves under the action of the gravitational field.
Spring Force
An important example of the above idea is a spring that obeys. Hooke's Law. Consider the situation shown in figure. One end of a spring is attached to a fixed vertical support and the other end to a block which can move on a horizontal table. Let x = 0 denote the position of the block when the spring is in its natural length.
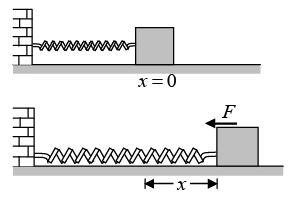
When the block is displaced by an amount x (either compressed or elongated) a restoring force (F) is applied by the spring on the block. The direction of this force F is always towards its mean position (x = 0) and the magnitude is directly proportional to x o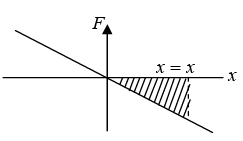
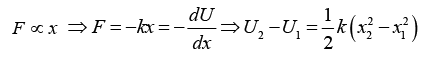
so potential energy of particle which is stored energy in spring is equivalent to u = 1/2kx2
Example 9: A mass m is shot vertically upward from the surface of the earth with initial speed v0. Assuming that the only force is gravity, find its maximum altitude and the minimum value of v0 for the mass to escape the earth completely.
The force on m is
The problem is one dimensional in the variable r and it is simple to find the kinetic energy at distance r by the work-energy theorem. Let the particle start at r = R, with initial velocity v0.
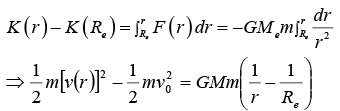
We can immediately find the maximum height of m . At the highest point, v (r) = 0 and we haveIt is a good idea to introduce known familiar constants whenever possible. For example
Since,
The escape velocity from the earth is the initial velocity needed to move rmax to infinity.
Then escape velocity, Vescape =
Example 10: Consider a mass M attached to a spring with spring constant k . Using the coordinate x measured from the equilibrium point x0 solve the Equation of motion for simple harmonic motion with the help of work energy theorem.
Consider a mass M attached to a spring. Using the coordinate x measured from the equilibrium point, the spring force is F = -kx
In order to find x and v, we must know their values at some time t0. Let us consider the case where at t = 0 the mass is released from rest, v0 = 0, at a distance x0 from the origin. Then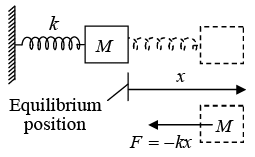
Separating the variables gives
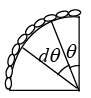
Example 11: A chain of length πr/r, mass per unit length ρ is released from rest at θ = 00. On a smooth surface. Find velocity of chain as it leaves the surface.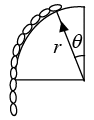
Taking a small element of chain taking angle dθ at point O, its mass = rdθ × ρ
P.E. of element = dm × g × h = rdθ × ρ × g × r cos θ
U1 = ρgr2
Final P.E. = mass of chain × g × distance moved by centre of gravity of chain
or gross in K.E. = Loss in P.E.
|
61 videos|23 docs|25 tests
|
FAQs on Linear Momentum & Energy - Mechanics & General Properties of Matter - Physics
| 1. What is linear momentum? |  |
| 2. What is the conservation of momentum? |  |
| 3. How does energy relate to linear momentum? |  |
| 4. What is the role of gravitation in linear momentum? |  |
| 5. How does the spring force affect linear momentum? |  |