Liveness Analysis | Compiler Design - Computer Science Engineering (CSE) PDF Download
Data-flow Analysis
Idea
Data-flow analysis derives information about the dynamic behavior of a program by only examining the static code
Examples:-
- How many registers do we need for the program on the right?
- Easy bound: the number of variables used (3)
- Better answer is found by considering the dynamic requirements of the program
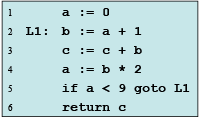
Liveness Analysis
➤ Definition:- A variable is live at a particular point in the program if its value at that point will be used in the future (dead, otherwise).
∴ To compute liveness at a given point, we need to look into the future
➤ Motivation: Register Allocation
- A program contains an unbounded number of variables
- Must execute on a machine with a bounded number of registers
- Two variables can use the same register if they are never in use at the same time (i.e, never simultaneously live).
∴ Register allocation uses liveness information
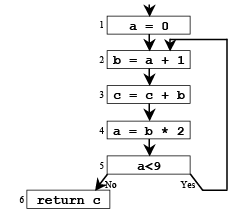
Liveness by Example
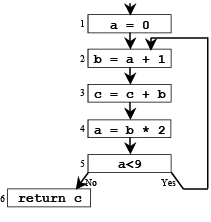
➤ What is the live range of b?
- Variable b is read in statement 4, so b is live on the (3 → 4) edge
- Since statement 3 does not assign into b, b is also live on the (2→3) edge
- Statement 2 assigns b, so any value of b on the (1→2) and (5→ 2) edges are not needed, so b is dead along these edges b’s live range is (2→3→4)
Liveness by Example (cont)
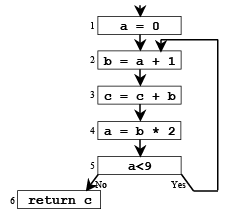
- Live range of a – a is live from (1→2) and again from (4→5→2) – a is dead from (2→3→4)
- Live range of b – b is live from (2→3→4)
- Live range of c – c is live from (entry→1→2→3→4→5→2, 5→6)
 Variables a and b are never simultaneously live, so they can share a register
Variables a and b are never simultaneously live, so they can share a register
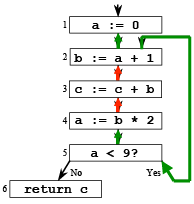
Control Flow Graphs (CFGs)
➤ Definition:- A CFG is a graph whose nodes represent program statements and whose directed edges represent control flow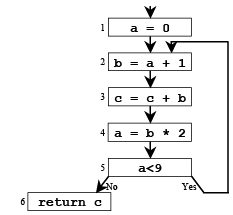
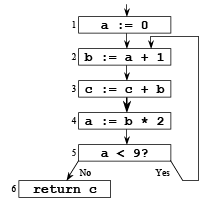
Examples
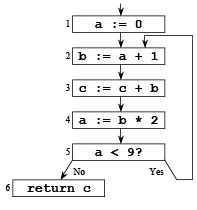
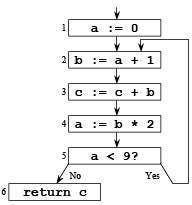
1 a := 0
2 L1: b := a + 1
3 c := c + b
4 a := b * 2
5 if a < 9 goto L1
6 return c
Terminology
➤ Flow Graph Terms
- A CFG node has out-edges that lead to successor nodes and in-edges that come from predecessor nodes
- pred[n] is the set of all predecessors of node n succ[n] is the set of all successors of node n
Examples
- Out-edges of node 5: (5→6) and (5→2)
- succ[5] = {2,6}
- pred[5] = {4}
- pred[2] = {1,5}
Uses and Defs
➤ Def (or definition)
- An assignment of a value to a variable
- def[v] = set of CFG nodes that define variable v
- def[n] = set of variables that are defined at node n
➤ Use
- A read of a variable’s value

- use[v] = set of CFG nodes that use variable v
- use[n] = set of variables that are used at node n
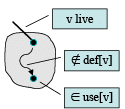
➤ More precise definition of liveness
- A variable v is live on a CFG edge if
(1) ∃ a directed path from that edge to a use of v (node in use[v]), and
(2) that path does not go through any def of v (no nodes in def[v])
The Flow of Liveness
➤ Data-flow
Liveness of variables is a property that flows through the edges of the CFG
➤ Direction of Flow
- Liveness flows backwards through the CFG, because the behavior at future nodes determines liveness at a given node
- Consider a
- Consider b
- Later, we’ll see other properties that flow forward
Liveness at Nodes
➤ We have liveness on edges- How do we talk about liveness at nodes?
➤ Two More Definitions- A variable is live-out at a node if it is live on any of that node’s outedges
A variable is live-in at a node if it is live on any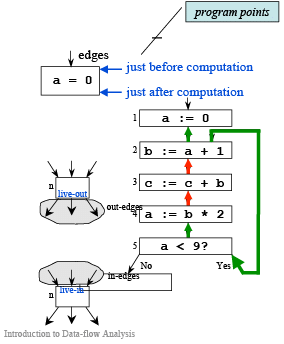
Computing Liveness
➤ Rules for computing liveness
(1) Generate liveness: If a variable is in use[n], it is live-in at node n 
(2) Push liveness across edges: If a variable is live-in at a node n then it is live-out at all nodes in pred[n] 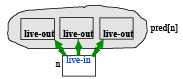
(3) Push liveness across nodes: If a variable is live-out at node n and not in def[n] then the variable is also live-in at n 
➤ Data-flow equations
Solving the Data-flow Equations
➤ Algorithm
This is iterative data-flow analysis (for liveness analysis)
➤ Example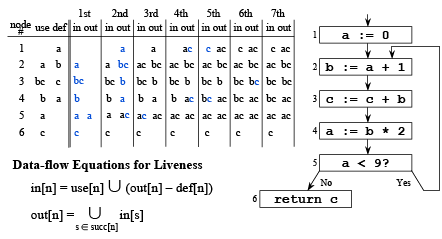
➤ Example (cont)
Data-flow Equations for Liveness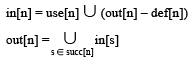
➤ Improving Performance
- Consider the (3→4) edge in the graph: out[4] is used to compute in[4] in[4] is used to compute out[3] . . .
- So we should compute the sets in the order: out[4], in[4], out[3], in[3], . . .
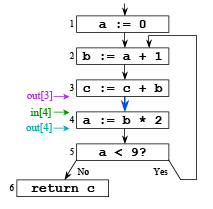 The order of computation should follow the direction of flow
The order of computation should follow the direction of flow
Iterating Through the Flow Graph Backwards
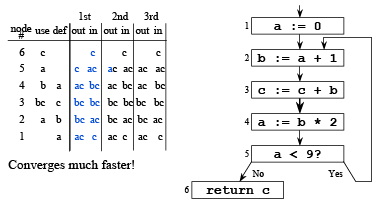
Solving the Data-flow Equations (reprise)
➤ Algorithm
Time Complexity
➤ Consider a program of size N
- Has N nodes in the flow graph and at most N variables
- Each live-in or live-out set has at most N elements
- Each set-union operation takes O(N) time
- The for loop body
- constant # of set operations per node
- O(N) nodes ⇒ O(N2) time for the loop
- Each iteration of the repeat loop can only make the set larger
- Each set can contain at most N variables ⇒ 2N2 iterations
➤ Worst case: O(N4)
Typical case: 2 to 3 iterations with good ordering & sparse sets ⇒ O(N) to O(N2)
More Performance Considerations
➤ Basic blocks
Decrease the size of the CFG by merging nodes that have a single predecessor and a single successor into basic blocks
➤ One variable at a time
Instead of computing data-flow information for all variables at once using sets, compute a (simplified) analysis for each variable separately
➤ Representation of sets
- For dense sets, use a bit vector representation
- For sparse sets, use a sorted list (e.g., linked list)
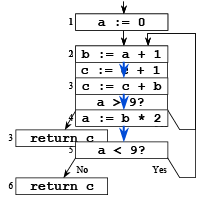
Conservative Approximation

➤ Solution X
Our solution as computed on previous slides
Conservative Approximation (cont)
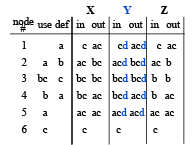
➤ Solution Y
- Carries variable d uselessly around the loop
- Does Y solve the equations?
- Is d live?
- Does Y lead to a correct program?
Imprecise conservative solutions ⇒ sub-optimal but correct programs
Conservative Approximation (cont)
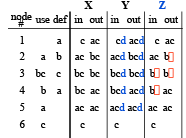
➤ Solution Z
- Does not identify c as live in all cases
- Does Z solve the equations?
- Does Z lead to a correct program?
Non-conservative solutions ⇒ incorrect programs
The Need for Approximations
➤ Static vs. Dynamic Liveness
- In the following graph, b*b is always non-negative, so c >= b is always true and a’s value will never be used after node 2
➤ Rule (2) for computing liveness
- Since a is live-in at node 4, it is live out at nodes 3 and 2
- This rule ignores actual control flow
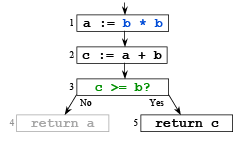
No compiler can statically know all a program’s dynamic properties!
Concepts
➤ Liveness
- Use in register allocation
- Generating liveness
- Flow and direction
- Data-flow equations and analysis
- Complexity
- Improving performance (basic blocks, single variable, bit sets)
➤ Control flow graphs
- Predecessors and successors
➤ Defs and uses
➤ Conservative approximation
- Static versus dynamic liveness
Next Time
➤ Reading
- Muchnick Ch. 7-7.5
➤ Think about. . .
- Other data-flow analyses
➤ Lecture
- Control-flow analysis
- Basic blocks and control-flow graphs
|
28 videos|86 docs|31 tests
|
FAQs on Liveness Analysis - Compiler Design - Computer Science Engineering (CSE)
| 1. What is liveliness analysis in computer science engineering? |  |
| 2. Why is liveliness analysis important in computer science engineering? |  |
| 3. What are the common challenges in liveliness analysis? |  |
| 4. How does liveliness analysis impact the performance of computer systems? |  |
| 5. What are some techniques used in liveliness analysis? |  |





















