Loci & Constructions | Mathematics for Grade 10 PDF Download
| Table of contents |

|
| Loci |

|
| Constructions between Points and Lines |

|
| Constructions: Bisecting Lines and Angles |

|
| Constructing Triangles |

|
| Bearings |

|
Loci
A locus is a path formed by a point which moves according to a rule. The plural is loci.
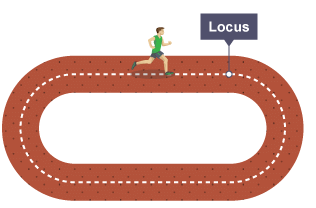 The runner is following a path. This path is a locus.
The runner is following a path. This path is a locus.Locus around a point
The hands of a clock move around the clock and create a locus.
The tip of each hand is always the same distance - equidistant - from the centre of the clock.
The locus the hands create is a circle.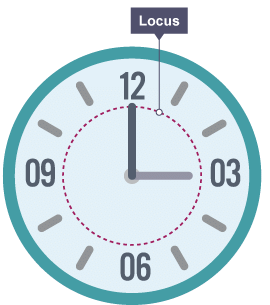
A locus of points at equal distance around a point is a circle.
A pair of compasses must be used to create a locus around a point.
Solved Example 1:
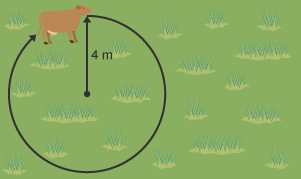
Farmer Smith has tied a cow around a post on a rope 4 m long. What the locus of the cow as it moves around the post?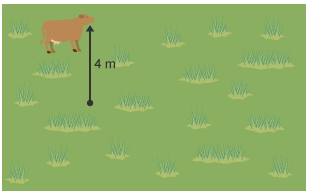
The locus is a circle 4 m from the post.
Locus from a line
A locus does not have to be a line - it can also be an area.
Example: A flowerbed runs along the grass between A and B. The edge of the flowerbed is 1 m from the grass. How would you draw an accurate diagram showing the flowerbed, using a scale of 1 cm:1 m? Draw a line parallel to AB 1 cm from AB. Shade in the area between this line and the line AB
Draw a line parallel to AB 1 cm from AB. Shade in the area between this line and the line AB The edge of the flowerbed is the locus from the line AB, because it is at a set distance from the line
The edge of the flowerbed is the locus from the line AB, because it is at a set distance from the line
Solved Example 2:
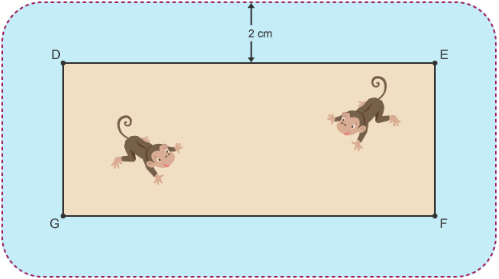
Visitors must stand at least 2 m away from the walls of the monkey enclosure at the zoo. How would you draw an accurate diagram to show where the visitors must not stand, using a scale of 1 cm:1 m?
Draw four lines parallel to each side of the rectangle, 2 cm away. Use a compass to draw rounded corners at D, E, F and G.
The straight line of the locus is parallel to the edges of the rectangle, because they are at a set distance from the edges. At each corner the locus is a quarter circle drawn from the fixed points D, E, F and G.
Visitors must not stand in the area between the rectangles. Shade this in.
Constructions between Points and Lines
Constructions are accurate diagrams drawn using a pair of compasses and a ruler.
When drawing constructions the construction lines must not be rubbed out.
Constructing the perpendicular from a point to a line
The shortest distance from a point to a line is the perpendicular distance.
Example: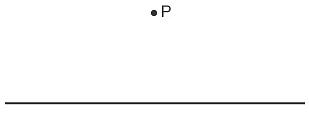 P is a point above a horizontal line. Construct the perpendicular from point P to the line
P is a point above a horizontal line. Construct the perpendicular from point P to the line Open a pair of compasses so the distance is slightly longer than the distance from P to the line. Place the compass at point P and draw two arcs, crossing the line either side of P
Open a pair of compasses so the distance is slightly longer than the distance from P to the line. Place the compass at point P and draw two arcs, crossing the line either side of P
Constructing the perpendicular from a point on a line
Example:
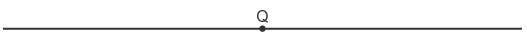 Q is a point on a line. Construct a perpendicular at Q
Q is a point on a line. Construct a perpendicular at Q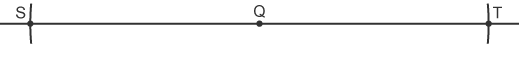 Put the compass point at Q. Draw two arcs crossing the line either side of Q
Put the compass point at Q. Draw two arcs crossing the line either side of Q
Constructions: Bisecting Lines and Angles
Constructing a perpendicular bisector
A plane flies at equal distance between two control towers.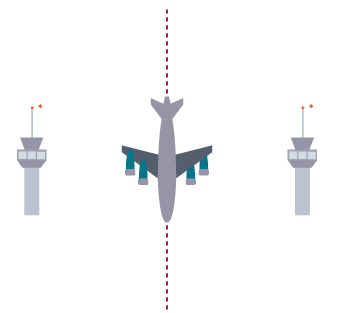
The locus of the plane is the perpendicular bisector of the two towers. When a line is divided into two equal lengths, it has been bisected.
Example: Draw the perpendicular bisector of the points X and Y
Draw the perpendicular bisector of the points X and Y Draw a line between the points
Draw a line between the points
Constructing the bisector of an angle
Example 1: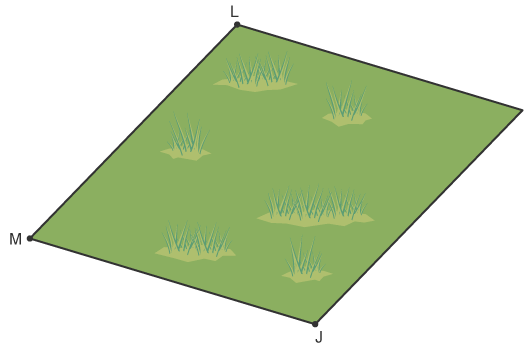 A path is constructed so it is at equal distance from the two edges of the field, JM and LM
A path is constructed so it is at equal distance from the two edges of the field, JM and LM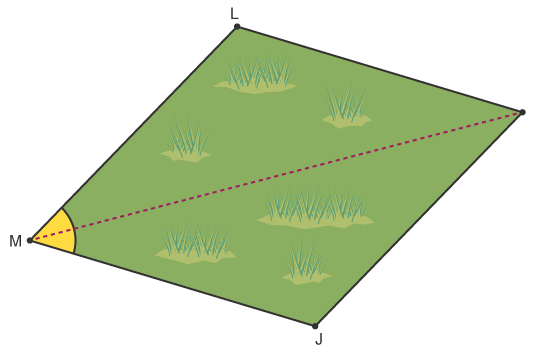 The locus of the path is the angle bisector of the angle LMJ. The path has separated the angle into two equal angles
The locus of the path is the angle bisector of the angle LMJ. The path has separated the angle into two equal angles
Example 2: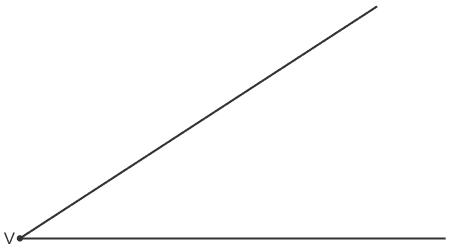 Bisect the angle V
Bisect the angle V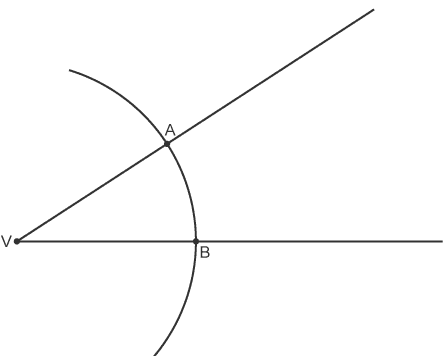 Place the compass point at V. Draw an arc to cross the two lines
Place the compass point at V. Draw an arc to cross the two lines
Solving problems using constructions
Problems can involve intersecting loci. It may be necessary to use several constructions to locate a region.
Example: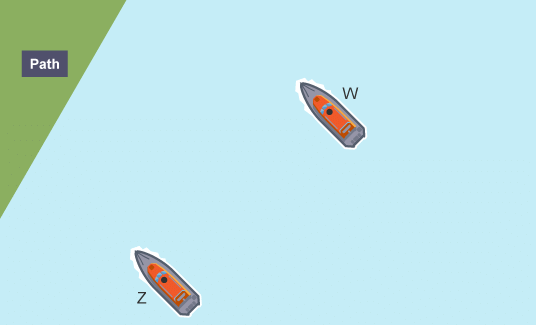 Two lifeboats are searching for a boat in distress. The boat is more than 40 m from the coastal path. It is closer to boat W than boat Z. Shade the region in which the boat lies. Use a scale of 1 cm:10 m
Two lifeboats are searching for a boat in distress. The boat is more than 40 m from the coastal path. It is closer to boat W than boat Z. Shade the region in which the boat lies. Use a scale of 1 cm:10 m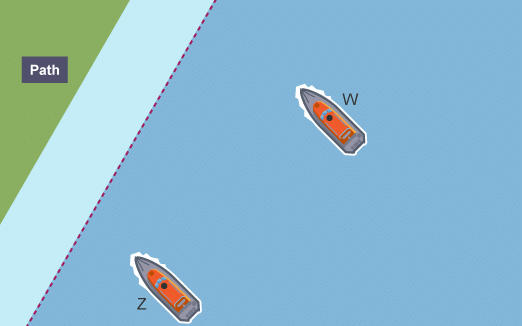 Draw a line parallel to the path 4 cm from the path. Shade in the area which is more than 4 cm from the path
Draw a line parallel to the path 4 cm from the path. Shade in the area which is more than 4 cm from the path
Constructing Triangles
Triangles and other shapes can be accurately constructed using a protractor, a pair of compasses and a ruler.
In order to draw a triangle, three properties are needed:
(i) SAS - Side Angle Side
(ii) ASA - Angle Side Angle
(iii) SSS - Side Side Side
Constructing triangles given SAS
The lengths of two sides and the size of the angle in between are needed.
Example:
Make an accurate drawing of a triangle with lengths 4 cm and 6 cm with an angle of 40° in between. Draw the longest side using a ruler
Draw the longest side using a ruler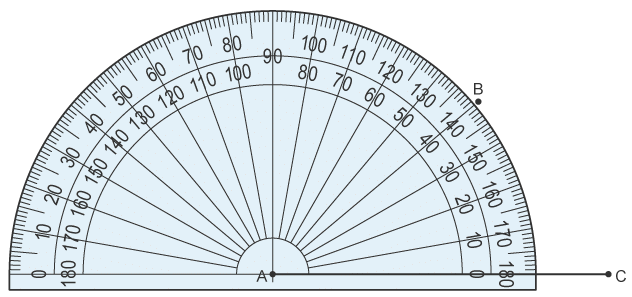
Use a protractor to measure the 40° angle. Put the centre of the protractor on the point A. Count from zero degrees from the horizontal line to 40° and put a mark at this point. This is point B
Constructing triangles given ASA
The sizes of two angles and the length of the side in between are needed.
Example:
Make an accurate drawing of a triangle with the angles 40° and 70°, with a side of length 8 cm in between. Draw the side using a ruler
Draw the side using a ruler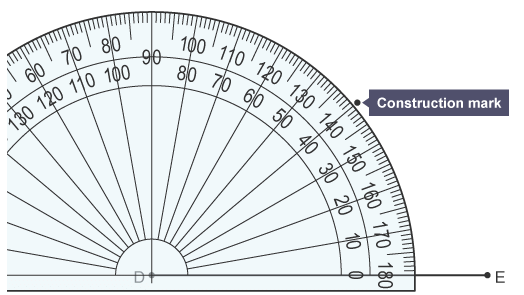
Use a protractor to measure the 40° angle. Put the centre of the protractor on point D. Count from zero degrees from the horizontal line to 40°. Put a construction mark at 40°
Constructing triangles given SSS
The lengths of all three sides are needed.
Example:
Make an accurate drawing of a triangle with sides of length 3 cm, 5 cm and 6 cm.
Draw the longest side using a ruler
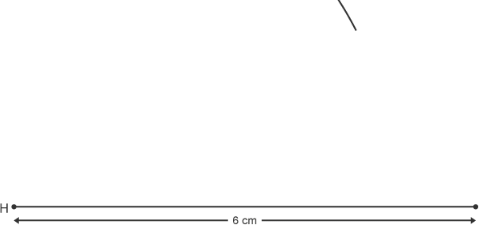 Open the pair of compasses until they are 5 cm wide. Use a ruler to measure it. Draw an arc from point H above the line
Open the pair of compasses until they are 5 cm wide. Use a ruler to measure it. Draw an arc from point H above the line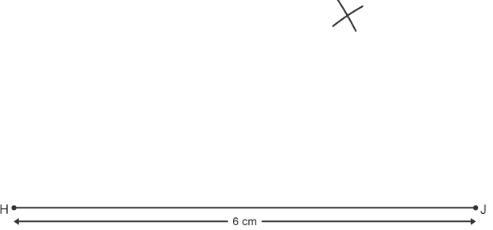 Open the pair of compasses until they are 3 cm wide. Use a ruler to measure it. Draw an arc from point J above the line
Open the pair of compasses until they are 3 cm wide. Use a ruler to measure it. Draw an arc from point J above the line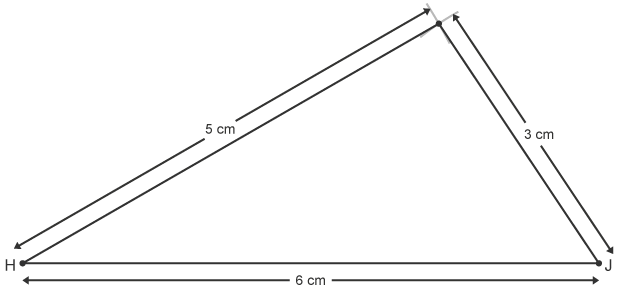 Join the arc to the points H and J using a ruler
Join the arc to the points H and J using a ruler
As with all constructions, ensure that the construction lines are not rubbed out. These show that the triangles were accurately constructed.
Bearings
There are four main directions on a compass; north, south, east and west. A compass can be used to describe a direction. Another method of describing directions is using bearings.
A compass can be used to describe a direction. Another method of describing directions is using bearings.
Ships use bearings to navigate. A bearing is measured in degrees.
A bearing:
(i) is measured from the north line
(ii) is measured clockwise
(iii) has three figures
For example, the bearing for the direction of east is 090°.
Example
This plane is flying at an angle of 48° from North. The bearing it flies at is 048°.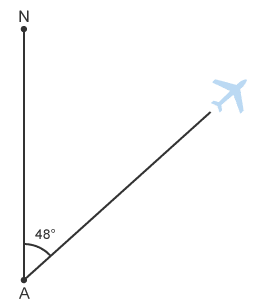 This plane is flying at an angle of 20° anticlockwise from North. Since a bearing is measured clockwise, the bearing it flies at is 360 - 20 = 340°.
This plane is flying at an angle of 20° anticlockwise from North. Since a bearing is measured clockwise, the bearing it flies at is 360 - 20 = 340°.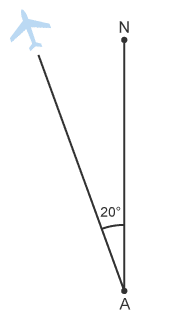
Solved Example:
Measure the bearing of the shark from the ship.
Method 1:
Draw a line between the ship and the shark. Draw a line pointing North from the ship.The shark is more than 180° clockwise from North. Place the centre of the protractor on the ship and 180° facing North.
Measure the angle clockwise from 0° to the line between the ship and the shark. In this case the measurement is 100°.
A bearing is measured from North. Add the angle to 180°:
180 + 100 = 280
The bearing of the shark from the ship is 280°.Method 2:
Draw a line between the ship and the shark. Draw a line pointing north from the ship.The shark is more than 180° from North. Place the centre of a protractor on the ship and 0° facing North.
Measure the angle anticlockwise from 0° to the line between the ship and the shark. In this case the measurement is 80°.
A bearing is measured clockwise from North. Subtract this angle from 360°.
360 - 80 = 280
The bearing of the shark from the ship is 280°.
|
137 videos|84 docs|44 tests
|