Class 9 Maths Chapter 7 Question Answers - Coordinate Geometry
Q1: If the points A(x, y), B(3, 6) and C(-3, 4) are collinear, show that x – 3y + 15 = 0.
Ans:
Pts. A(x, y), B(3, 6), C(-3, 4) are collinear.
∴ Area of ∆ = 0
As area of ∆
= 12[ x 1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
∴Area of ∆ABC
= x(6 – 4) + 3(4 – y) + (-3) (y – 6) = 0
= 2x + 12 – 3y – 3y + 18 = 0
= 2x – 6y + 30 = 0
∴ x – 3y + 15 = 0
Q2: If two vertices of an equilateral triangle are (3, 0) and (6, 0), find the third vertex. (2011D)
Ans:
Let A (3,0), B (6, 0), C (x, y).
∴ ∆ABC is an equilateral
∴ AB = BC = AC
AB2 = BC2 = AC2 …[Squaring throughout
(6 – 3)2 + (0 – 0)2 = (x – 6)2 + (1 – 0)2 = (x – 3)2 + (y – 0)2
9 = x2 – 12x + 36 + y2 = x2 – 6x + 9 + y2
Q3: If the vertices of a triangle are (1, -3), (4, p) and (-9, 7) and its area is 15 sq. units, find the value(s) of p.
Ans:
Area of ∆ = 15 sq. units
12 [1(p – 7) + 4(7 + 3)) + (-9)(-3 – p)] = ±15
p – 7 + 40 + 27 + 9p = ±30
10p + 60 = ± 30
10p = -60 ± 30
p = −60±30 / 10
∴ Taking +ve sign, p = −60 + 30 / 10 = −30 / 10 = -3
Taking -ve sign, p = −60 − 30 / 10 = −90 / 10 = -9
Q4: If A(4, 2), B(7,6) and C(1, 4) are the vertices of a AABC and AD is its median, prove that the median AD divides AABC into two triangles of equal areas.
Ans: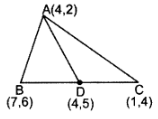
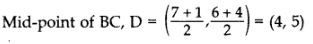
Area of ∆ABD
= 1/2 (x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= 1/2[4(6 – 5) + 7(5 – 2) + 4(2 – 6))
= 1/2(4 + 21 – 16) = 9/2 sq.units …(i)
Area of ∆ADC
= 1/2 [4(5 – 4) + 4(4 – 2) + 162 – 5)]
= 1/2(4 + 8 – 3) = 9/2sq.units
From (i) and (ii),
Area of ∆ABD = Area of ∆ADC
∴ Median AD divides ∆ABC into two triangles of equal area.
Q5: Prove that the area of a triangle with vertices (t, t – 2), (t + 2, t + 2) and (t + 3, t) is independent of t.
Ans:
Let A(t, t – 2), B(t + 2, + + 2), C(t + 3, t).
Area of ∆ABC
= 1/2[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= 1/2 [t(t + 2 – t) + (t + 2)(t – (t – 2)) +(t + 3)((t – 2) – (t + 2))]
= 1/2 [t(2) + (t + 2)(2) + (t + 3)(-4)]
= 1/2 (2+ + 2+ + 4 – 46 – 12]
= 1/2 [-8]
= -4
Area of ∆ is always positive.
∴ Area of ∆ = 4 sq. units, which is independent of t.
Q6: If the area of triangle ABC formed by A(x, y), B(1, 2) and C(2, 1) is 6 square units, then prove that x + y = 15 or x + y = -9.
Ans:
Let A(x, y), B(1, 2), C(2, 1).
Area of ∆ABC = 6 sq. units …[Given
As 1/2 [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)] = 6
∴ x(2 – 1) + 1(1 – y) + 2(y – 2) = ±12
x + 1 – y + 2y – 4 = ±12
Taking +ve sign
x + y = 12 + 4 – 1
∴ x + y = 15
Taking -ve sign
x + y = -12 + 4 – 1
∴ x + y = -9
Q7: Point P(x, 4) lies on the line segment joining the points A(-5, 8) and B(4, -10). Find the ratio in which point P divides the line segment AB. Also find the value of x.
Ans:
Q8: Find the ratio in which the point P(x, 2) divides the line segment joining the points A(12, 5) and B(4, -3). Also, find the value of x.
Ans:
Q9: Find the area of the quadrilateral ABCD whose vertices are A(-3, -1), B(-2, -4), C(4, -1) and D(3, 4).
Ans: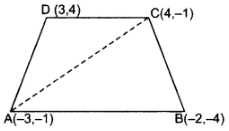 Area of ∆ = 12[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
Area of ∆ = 12[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
∴ Area of ∆ABC
= 1/2[(-3)(4 + 1) + (-2){-1 – (-1)} +4{-1 – (- 4}}]
= 1/2[9+ 0 + 12] = 21 sq. units …(i)
∴ Area of ∆ACD
= 1/2[-3(-1 – 4) + 4{(4 – (-1)} + 34{-1 – (-1)}]
= 1/2 [15 + 20 + 0]
= 1/2[15 + 20] = 35/2 sq. units
∴ ar(quad. ABCD) = ar (∆ABC) + ar(∆ACD)
= 21/2+35/2 …[From (i) & (ii)
= 56/2 = 28 sq. units
Q10: If the points A(1, -2), B(2, 3), C(-3, 2) and D(-4, -3) are the vertices of parallelogram ABCD, then taking AB as the base, find the height of this parallelogram.
Ans: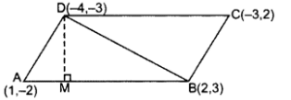 1st method. A(1, -2), B(2, 3), D(-4, -3)
1st method. A(1, -2), B(2, 3), D(-4, -3)
.. Area of ∆ABD
= 1/2 [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= 1/2 [1(3 + 3) + 2(-3 + 2) + (-4)(-2 – 3)]
= 1/2 [6 – 2 + 20) = 242 sq.units
ar(∆ABD) = 12 sq.units
= 1/2 × AB × DM = 12 sq.units …[Area of ∆ = 1/2 × Base × Altitude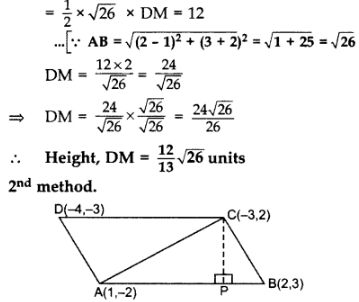
Q11: If P(2, 4) is equidistant from Q(7, 0) and R(x, 9), find the values of x. Also find the distance P.
Ans: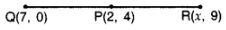 PQ = PR …[GivenPQ2 = PR2 … [Squaring both sides
PQ = PR …[GivenPQ2 = PR2 … [Squaring both sides
∴ (7 – 2)2 + (0 – 4)2 = (x – 2)2 + (9 – 4)2
⇒ 25 + 16 = (x – 2)2 + 25
⇒ 16 = (x – 2)2
⇒ ±4 = x – 2 …[Taking sq. root of both sides
⇒ 2 ± 4 = x
⇒ x = 2 + 4 = 6 or x = 2 – 4 = -2
Q12: Find the value of k, if the points P(5, 4), Q(7, k) and R(9, – 2) are collinear.
Ans:
Given points are P(5, 4), Q(7, k) and R(9, -2).
x1 (y2 – y3) + x2(y3 – y1) + x3(y1 – y2) = 0 …[∵ Points are collinear
∴ 5 (k + 2) + 7 (- 2 – 4) + 9 (4 – k) = 0
5k + 10 – 14 – 28 + 36 – 9k = 0
4 = 4k ∴ k=1
Q13: If (3, 3), (6, y), (x, 7) and (5, 6) are the vertices of a parallelogram taken in order, find the values of x and y.
Ans:
Let A (3, 3), B (6, y), C (x, 7) and D (5, 6).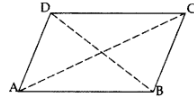
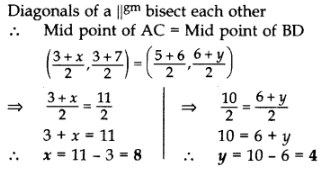
Q14: A point P divides the line segment joining the points A(3, -5) and B(-4, 8) such that AP/PB=K/1. If P lies on the line x + y = 0, then find the value of K.
Ans: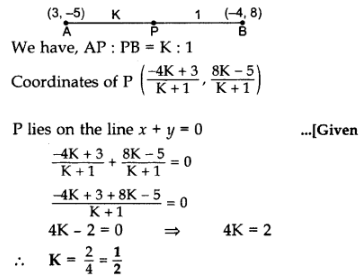
Q15: If the centroid of ∆ABC, in which A(a, b), B(b, c), C(c, a) is at the origin, then calculate the value of (a3 + b3 + c).
Ans: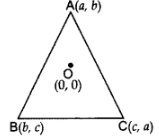 Centroid =
Centroid = 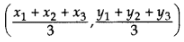
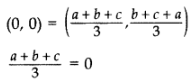
a + b + c = 0
If a + b + c = 0
then, as we know
a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ac)
∴ a3 + b3 + c3 – 3abc = 0 … [Since a + b + c = 0
∴ a3 + b3 + c3 = 3abc …(Hence proved)
Q16: Find the values of k so that the area of the triangle with vertices (k + 1, 1), (4, -3) and (7, -k) is 6 sq. units.
Ans:
Let A(k + 1, 1), B(4, -3) and C(7, -k).
We have, Area of ∆ABC = 6 … [Given
6 = 1/2 [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
6 = 1/2[(k + 1)(-3 + k) + 4(-k – 1) + 7(1 + 3)]
12 = (-3k + k2 – 3 + k – 4k – 4 + 28]
12 = [k2 – 6k + 21]
⇒ k2 – 6k + 21 – 12 = 0
⇒ k2 – 6k + 9 = 0
⇒ k2 – 3k – 3k + 9 = 0
⇒ k(k – 3) – 3(k – 3) = 0 =
⇒ (k – 3) (k – 3) = 0
⇒ k – 3 = 0 or k – 3 = 0
⇒ k = 3 or k = 3
Solving to get k = 3.
Q17: For the triangle ABC formed by the points A(4, -6), B(3,-2) and C(5, 2), verify that median divides the triangle into two triangles of equal area.
Ans:
Let A(4, -6), B(3, -2) and C(5, 2) be the vertices of ∆ABC.
Since AD is the median
∴ D is the mid-point of BC.
⇒ D(3 + 5 / 2,−2 + 2 / 2) ⇒ D(4,0)
Area of ∆ABD
= 1/2 [4(-2 – 0) + 3(0 + 6) + 4(-6 + 2)]
= 1/2 [-8 + 18 – 16) = 1/2 [-6] = -3
But area of A cannot be negative.
∴ ar(∆ABD) = 3 sq.units …(i)
Area of ∆ADC
= 1/2 [4(0 – 2) + 4(2 + 6) + 5(-6 – 0)]
= 1/2(-8 + 32 – 30] = 12 [-6] = -3
But area of ∆ cannot be negative.
∴ ar(∆ADC) = 3 sq.units
From (i) and (ii),
∴ Median AD of AABC divides it into two ∆s of equal area.
Q18: Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are A(2, 1), B(4, 3) and C(2, 5).
Ans: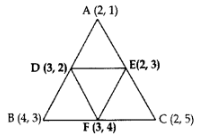

Q19: Find the values of k for which the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k) are collinear.
Ans:
A (k + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k).
When points are collinear, area of ∆ is 0.
∴ Area of triangle = 0
⇒ [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)] = 0
⇒ [(k + 1) (2k + 3 – 5k) + 3k (5k – 2k) + (5k – 1) (2k – 2k – 3)] = 0
⇒ [(k + 1) (3 – 3k) + 3k(3k) + (5k – 1)(-3)] = 0
⇒ [3k – 3k2 + 3 – 3k + 9k2 – 15k + 3) = 0
⇒ 6k2 – 15k + 6 = 0
⇒ 2k2 – 5k + 2 = 0
⇒ 2k2 – 4k – 1k + 2 = 0
⇒ 2k(k – 2) – 1(k – 2) = 0
⇒ (k – 2)(2k – 1) = 0
⇒ k – 2 = 0 or 2k – 1 = 0
⇒ k = 2 or k = 1/2
We get, k = 2, 1/2
|
40 videos|471 docs|57 tests
|

















