Class 8 Exam > Class 8 Notes > Mathematics Class 8- New NCERT (Ganita Prakash) > MCQ (with Solutions): Quadrilaterals
MCQ (with Solutions): Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Q1. Which of the following quadrilaterals has two pairs of adjacent sides equal and diagonals intersecting at right angles?
(i) square
(ii) rhombus
(iii) kite
(iv) rectangle.
Q2. Which of the following quadrilaterals has a pair of opposite sides parallel?
(i) rhombus
(ii) trapezium
(iii) kite
(iv) rectangle.
Q3. Which of the following quadrilaterals is a regular quadrilateral?
(i) rectangle
(ii) square
(iii) rhombus
(iv) kite.
Q4. Which of the quadrilaterals has all angles as right angles, opposite sides equal and diagonals bisect each other?
(i) rectangle
(ii) rhombus
(iii) square
(iv) none of these.
Q5. Which of the parallelograms has all sides equal and diagonals bisect each other at a right angle?
(i) square
(ii) rectangle
(iii) rhombus
(iv) trapezium.
Q6. In an isosceles parallelogram, we have:
(i) pair of parallel sides as equal
(ii) pair of non-parallel sides as equal
(iii) pair of non-parallel sides as perpendicular
(iv) none of these.
Q7. Which of the following is true the adjacent angles of a parallelogram?
(i) they are equal to each other
(ii) they are complementary angles
(iii) they are supplementary angles
(iv) none of these.
Q8. The sides of a pentagon are produced in order. Which of the following is the sum of its exterior angles?
(i) 540°
(ii) 180°
(iii) 720°
(iv) 360°
Q9. Which of the following is a formula to find the sum of interior angles of a quadrilaters of n-sides?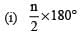
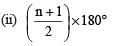
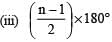
(iv) (n – 2) × 180°
Q10. Diagonals of which of the following quadrilaterals do not bisect it into two congruent triangles?(i) rhombus
(ii) trapezium
(iii) square
(iv) rectangle.
Answers
1. (iii)
2. (ii)
3. (ii)
4. (i)
5. (iii)
6. (ii)
7. (iii)
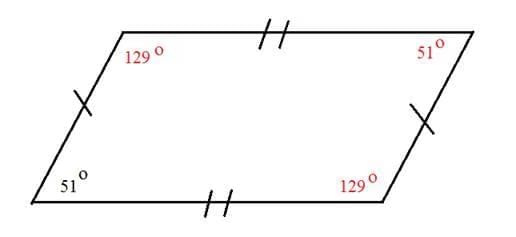Supplementary angles
8. (iv)
9. (iv)
10. (ii)
The document MCQ (with Solutions): Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash) is a part of the Class 8 Course Mathematics Class 8- New NCERT (Ganita Prakash).
All you need of Class 8 at this link: Class 8
|
26 videos|177 docs|11 tests
|
FAQs on MCQ (with Solutions): Quadrilaterals - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What are the properties of a quadrilateral? |  |
Ans. A quadrilateral is a polygon with four sides, four vertices, and four angles. The sum of the internal angles in a quadrilateral is always 360 degrees. Quadrilaterals can be classified into different types such as squares, rectangles, trapezoids, and rhombuses, each having unique properties. For example, a rectangle has opposite sides equal and all angles equal to 90 degrees, while a rhombus has all sides equal and opposite angles equal.
| 2. How can we classify quadrilaterals based on their sides and angles? | |
Ans. Quadrilaterals can be classified based on their sides and angles into several categories:
1. Parallelograms: Opposite sides are equal and parallel.
2. Rectangles: All angles are right angles, and opposite sides are equal.
3. Rhombuses: All sides are equal, and opposite angles are equal.
4. Squares: All sides and angles are equal.
5. Trapezoids: At least one pair of opposite sides is parallel.
6. Kite: Two pairs of adjacent sides are equal.
| 3. What is the formula to find the area of a quadrilateral? | |
Ans. The area of a quadrilateral can be calculated using various methods depending on its type. For a rectangle, the area is calculated as length × width. For a trapezoid, the area can be calculated using the formula: Area = (1/2) × (base₁ + base₂) × height. For irregular quadrilaterals, the area can be found by dividing it into triangles or using the shoelace formula.
| 4. What is the difference between convex and concave quadrilaterals? | |
Ans. Convex quadrilaterals have all interior angles less than 180 degrees, and the diagonals lie inside the shape. In contrast, concave quadrilaterals have one or more interior angles greater than 180 degrees, causing at least one diagonal to lie outside the shape. This distinction is important in geometry as it affects the properties and classifications of quadrilaterals.
| 5. How do you calculate the perimeter of a quadrilateral? | |
Ans. The perimeter of a quadrilateral is calculated by adding the lengths of all four sides. The formula can be expressed as: Perimeter = side₁ + side₂ + side₃ + side₄. If the lengths of the sides are known, simply sum them up to find the total perimeter of the quadrilateral.
About this Document
4.73/5
Rating
Oct 02, 2025
Last updated
Related Exams
Document Description: MCQ (with Solutions): Quadrilaterals for Class 8 2025 is part of Mathematics Class 8- New NCERT (Ganita Prakash) preparation.
The notes and questions for MCQ (with Solutions): Quadrilaterals have been prepared according to the Class 8 exam syllabus. Information about MCQ (with Solutions): Quadrilaterals covers topics
like and MCQ (with Solutions): Quadrilaterals Example, for Class 8 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for MCQ (with Solutions): Quadrilaterals.
Introduction of MCQ (with Solutions): Quadrilaterals in English is available as part of our Mathematics Class 8- New NCERT (Ganita Prakash)
for Class 8 & MCQ (with Solutions): Quadrilaterals in Hindi for Mathematics Class 8- New NCERT (Ganita Prakash) course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: MCQ (with Solutions): Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash)
Description
Full syllabus notes, lecture & questions for MCQ (with Solutions): Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash) - Class 8 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 8- New NCERT (Ganita Prakash) | Best notes, free PDF download
Information about MCQ (with Solutions): Quadrilaterals
In this doc you can find the meaning of MCQ (with Solutions): Quadrilaterals defined & explained in the simplest way possible. Besides explaining types of
MCQ (with Solutions): Quadrilaterals theory, EduRev gives you an ample number of questions to practice MCQ (with Solutions): Quadrilaterals tests, examples and also practice Class 8
tests
Related Searches
study material
,Important questions
,Previous Year Questions with Solutions
,Summary
,MCQs
,mock tests for examination
,Free
,Exam
,Sample Paper
,video lectures
,Extra Questions
,past year papers
,Viva Questions
,ppt
,shortcuts and tricks
,MCQ (with Solutions): Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash)
,MCQ (with Solutions): Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash)
,Semester Notes
,practice quizzes
,Objective type Questions
,MCQ (with Solutions): Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash)
;
Additional Information about MCQ (with Solutions): Quadrilaterals for Class 8 Preparation
MCQ (with Solutions): Quadrilaterals Free PDF Download
The MCQ (with Solutions): Quadrilaterals is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the MCQ (with Solutions): Quadrilaterals now and kickstart your journey towards success in the Class 8 exam.
Importance of MCQ (with Solutions): Quadrilaterals
The importance of MCQ (with Solutions): Quadrilaterals cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
MCQ (with Solutions): Quadrilaterals Notes
MCQ (with Solutions): Quadrilaterals Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to MCQ (with Solutions): Quadrilaterals.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, MCQ (with Solutions): Quadrilaterals Notes on EduRev are your ultimate resource for success.
MCQ (with Solutions): Quadrilaterals Class 8 Questions
The "MCQ (with Solutions): Quadrilaterals Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study MCQ (with Solutions): Quadrilaterals on the App
Students of Class 8 can study MCQ (with Solutions): Quadrilaterals alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the MCQ (with Solutions): Quadrilaterals,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of MCQ (with Solutions): Quadrilaterals is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily