MID POINT THEOREM - Class 9 PDF Download
State and prove mid point theoram?
Ref: https://edurev.in/question/780466/State-and-prove-mid-point-theoram-
MID POINT THEORAM
Geometry is one among the fundamental and essential branches of mathematics. This field deals with the geometrical problems and figures which are based on the properties. One of the important theorems in the field of geometry that deals with the properties of triangles are called as the Mid- Point Theorem.
The theory of midpoint theorem is used in the coordinate geometry stating that the midpoint of the line segment is an average of the endpoints. To solve an equation by the use of this Theorem, it is important that both the ‘x’ and the ‘y’ coordinates should be known. The Mid- Point Theorem is also useful in the fields of calculus and algebra.
Statement and Proof of Mid Point Theorem
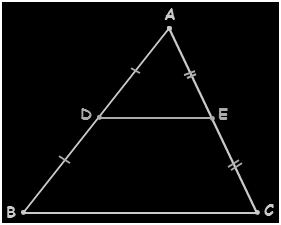
Statement – “The line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the triangle.”
Mid Point Theorem Proof
If midpoints of any of the sides of a triangle are adjoined by the line segment, then the line segment is said to be in parallel to all the remaining sides and also will measure about half of the remaining sides.
Consider the triangle ABC, as shown in the above figure,
Let E and D be the midpoints of the sides AC and AB. Then the line DE is said to be parallel to the sides BC, whereas the side DE is half of the side BC; i.e.
DE is parallel to BC
DE∥BC
DE = (1/2 * BC).
Now consider the below figure,
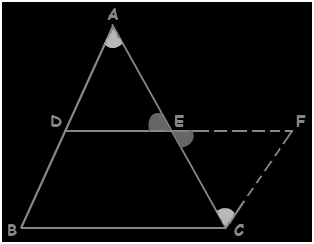
Construction- Extend the line segment DE and produce it to F such that, EF=DE.
In the triangle, ADE, and also the triangle CFE
EC= AE —– (given)
∠CEF = ∠AED {vertically opposite angles}
EF = DE { by construction}
hence,
△ CFE ≅ △ ADE {by SAS}
Therefore,
∠CFE = ∠ADE {by c.p.c.t.}
∠FCE= ∠DAE {by c.p.c.t.}
and CF = AD {by c.p.c.t.}
The angles, ∠CFE and ∠ADE are the alternate interior angles. Assume CF and AB as two lines which are intersected by the transversal DF.
In a similar way, ∠FCE and ∠DAE are the alternate interior angles. Assume CF and AB are the two lines which are intersected by the transversal AC.
Therefore, CF∥AB
So, CF∥BD
and CF = BD {since BD = AD, it is proved that CF = AD}
Thus, BDFC forms a parallelogram.
By the use of properties of a parallelogram, we can write
BC∥DF
and BC = DF
BC∥DE
and DE = (1/2 * BC). Hence Proved.
The Mid- Point Theorem can also be proved by the use of triangles. The line segment which is on the angle, suppose two lines are drawn in parallel to the x and the y-axis which begin at endpoints and also the midpoint, then the result is said to be two similar triangles. This relation of these triangles forms the Mid- Point Theorem.
FAQs on MID POINT THEOREM - Class 9
| 1. What is the Midpoint Theorem? |  |
| 2. How can the Midpoint Theorem be proven? |  |
| 3. Can the Midpoint Theorem be applied to any line segment? |  |
| 4. How is the Midpoint Theorem useful in geometry? |  |
| 5. Are there any real-life applications of the Midpoint Theorem? |  |














