Magnetic Field on the Axis of a Circular Current Loop | Physics for JEE Main & Advanced PDF Download
4. MAGNETIC FIELD AT AN AXIAL POINT OF A CIRCULAR COIL
Consider a circular loop of radius R and carrying a steady current i. We have to find out magnetic field at the axial point P, which is at distance x from the centre of the loop.
Consider an element i of the loop as shown in figure, and the distance of point P from current element is r. The magnetic field at P due to this current element from the equation (1) can be given by,
In case of point on the axis of a circular coil, as for every current element there is a symmetrically situated opposite element, the component of the field perpendicular to the axis cancel each other while along the axis add up.
Therefore, =
Here, q is angle between the current element id and , which is everywhere and
sin 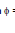 =
= =
Therefore, B =
or, B =
or, B = ...(4)
If the coil has N turns, then
B =
Direction of 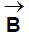 : Direction of magnetic field at a point the axis of a circular coil is along the axis and its orientation can be obtained by using the right-hand thumb rule. If the figures are curled along the current, the stretched thumb will point towards the magnetic field.
: Direction of magnetic field at a point the axis of a circular coil is along the axis and its orientation can be obtained by using the right-hand thumb rule. If the figures are curled along the current, the stretched thumb will point towards the magnetic field.
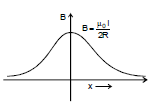
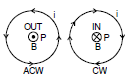
Magnetic field will be out of the page for anticlockwise current while into the page for clockwise current as shown in the figure given. Now consider some special cases involving the application of equation (4)
Case I : Field at the centre of the coil
In this case distance of the point P from the centre (x) = 0, the magnetic field
B = =
Case II : Field at a point far away from the centre
It means x >> R, B =
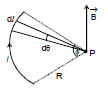
4.1 FIELD AT THE CENTRE OF A CURRENT ARC
Consider an arc of radius R carrying current i and subtending an angle f at the centre.
According to Biot-Savart Law, the magnetic field induction at the point P is given by
B =
Here, dl = Rdθ
Therefore, B =
or, B = ...(5)
It `l' is the length of the circular arc, we have
B = ...(6)
Consider some special cases involving the application of equation (5)
case I : If the loop is semicircular
In this case 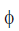 = π, so
= π, so
B = 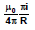
and will be out of the page for anticlockwise current while into the page for clockwise current as shown in the figure.
Case II. If the loop is a full circle with N turns
In this case 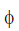 = 2p, so
= 2p, so
B =
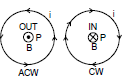
and will be out of the page for anticlockwise current while into the page for clockwise current as shown in the figure.
Ex.7 Two wire loop PQRSP formed by joining two semicircular wires of radii R1 and R2 carries a current i as shown in the figure given below. What is the magnetic field induction at the centre O in cases (A) and (B) ?
Sol. (a) As the point O is along the length of the straight wires, so the field at O due to them will be zero and hence magnetic field is only due to semicircular portions
Therefore,
or, =
out of the page
(b) =
into the page
Ex.8 A battery is connected between two points A and B on the circumference of a uniform conducting ring of radius r and resistance R as shown in the figure given below. One of the arcs AB of the ring subtends an angle q at the centre. What is the value of the magnetic field at the centre due to the current in the ring?
Sol. (a) As the field due to arc at the centre is given by
B =
Therefore, B =
But (VA - VB) = i1R1 = i2R2
or, i2 = i1 = i1
[Therefore, R µ L]
i2 = i1 [Therefore, L = rq]
Therefore, BR =
i.e., the field at the centre of the coil is zero and is independent of θ.
Ex.9 A charge of one coulomb is placed at one end of a nonconducting rod of length 0.6m. The rod is rotated in a vertical plane about a horizontal axis passing through the other end of the rod with angular frequency 104π rad/s. Find the magnetic field at a point on the axis of rotation at a distance of 0.8 m from the centre of the path.
Now half of the charge is removed from one end and placed on the other end. The rod is rotated in a vertical plane about horizontal axis passing through the mid-point of the rod with the same angular frequency. Calculate the magnetic field at a point on the axis at a distance of 0.4 m from the centre of the rod.
Sol. As the revolving charge q is equivalent to a current
i = qf = q × = 1 ×
= 5 × 103 A
Now B =
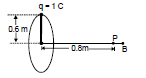
Therefore, B = 10-7 × = 1.13 × 10-3 T
If half of the charge is placed at the other end and the rod is rotated at the same frequency, the equivalent current.
i' = = qf = i = 5 × 103 A
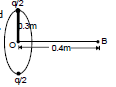
In this case, R' = 0.3 m and x' = 0.4 m
Therefore, B' = 10-7 × = 2.3 × 10-3T
5. Solenoid :
(i) Solenoid contains large number of circular loops wrapped around a non-conducting cylinder. (it may be a hollow cylinder or it may be a solid cylinder)
(ii) The winding of the wire is uniform direction of the magnetic field is same at all points of the axis.
(iii) on axis (turns should be very close to each others).
B = ...(7)
where n : number of turns per unit length.
cosθ1 = ; cosβ =
= -cosθ2
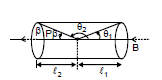
B =
=
Derivation :
Take an element of width dx at a distance x from point P. [point P is the point on axis at which we are going to calculate magnetic field. Total number of turns in the element dn = ndx where n : number of turns per unit length]
dB =
B =
|
268 videos|732 docs|171 tests
|
FAQs on Magnetic Field on the Axis of a Circular Current Loop - Physics for JEE Main & Advanced
| 1. What is the formula to calculate the magnetic field on the axis of a circular current loop? |  |
| 2. How does the magnetic field on the axis of a circular current loop vary with distance? |  |
| 3. Does the direction of the magnetic field on the axis of a circular current loop change with distance? |  |
| 4. How does the current flowing through the loop affect the magnetic field on its axis? |  |
| 5. Can the magnetic field on the axis of a circular current loop be zero? |  |
















