Mathematics: CBSE Sample Question Paper (2020-21)- 1 | Mathematics (Maths) Class 12 - JEE PDF Download
| Table of contents |

|
| PART - A |

|
| Section- I |

|
| Section - II |

|
| PART - B |

|
| Section - III |

|
| Section - IV |

|
| Section - V |

|
Class - XII
Math
TIME: 3 Hrs.
M.M: 80
General Instructions:
1. This question paper contains two parts A and B. Each part is compulsory. Part A carries 24 marks and Part B carries 56 marks.
2. Part-A has Objective Type Questions and Part-B has Descriptive Type Questions.
3. Both Part A and Part B have choices.
Part – A :
1. It consists of two sections- I and II.
2. Section I comprises of 16 very short answer type questions.
3. Section II contains 2 case studies. Each case study comprises of 5 case-based MCQs. An examinee is to attempt any 4 out of 5 MCQs.
Part – B :
1. It consists of three sections-III, IV and V.
2. Section III comprises of 10 questions of 2 marks each.
3. Section IV comprises of 7 questions of 3 marks each.
4. Section V comprises of 3 questions of 5 marks each.
5. Internal choice is provided in 3 questions of Section –III, 2 questions of Section -IV and 3 questions of Section-V. You have to attempt only one of the alternatives in all such questions.
PART - A
Section- I
Question numbers 1 to 16 are very short answer type questions.
Q.1. What is the principal value branch of cos–1 x ?
Ans. As we know that the principal value of cos–1x is [0, π].
y = cos–1x
Q.2. If A is a 3 × 3 matrix such that |A| = 8, then find |3A|.
Ans. Here |A| = 8
Then |3A| = 33|A| = 27 × 8 = 216
OR
Give an example of a skew symmetric matrix of order 3.
Ans. Skew symmetric matrix : A square matrix A = [aij] is said be a skew symmetrix matrix if AT = –A i.e., if A = [ay], then if A is skew symmetrix then AT = –[aij] or AT = –A.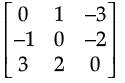
Q.3. If [x 1] 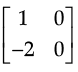 = 0, then find the value of x.
= 0, then find the value of x.
Ans.
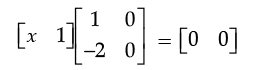
⇒ [ x - 2 0] = [ 0 0]
⇒ x - 2 = 0 [ By def. of equality]
⇒ x = 2
OR
If A is a square matrix such that A2 = A, then write the value of 7A – (I + A)3, where I is an identity matrix.
Ans. 7A – (I + A)3 = – I
Detailed Solution:
Since, A2 = A,
∴ 7A – (I + A)3 = 7A – I3 – 3A2I – 3AI2 – A3
= 7A – I – 3A – 3A – A2A
= 7A – I – 3A – 3A – A·A
= 7A – I – 3A – 3A – A
= 7A – I – 7A = – I
Q.4. If A and B are symmetric matrices of same order, then find AB – BA.
Ans. Given that, A and B are symmetric matrices.
⇒ A = A’ and B = B’,
Now (AB – BA)’ = (AB)’ – (BA)’ (i)
⇒ (AB – BA)’ = B’A’ – A’B’ [By reversal law]
⇒ (AB – BA)’ = BA – AB [From Eq. (i)]
⇒ (AB – BA)’ = –(AB – BA)
⇒ (AB – BA) is a skew matrix.
Q.5. If 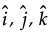 are unit vectors along three mutually perpendicular directions, then find
are unit vectors along three mutually perpendicular directions, then find 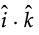 .
.
Ans.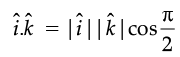 = 1 × 1 × 0 = 0
= 1 × 1 × 0 = 0
Q.6. On what set the function f(x) = cot x is discontinuous?
Ans. Given that,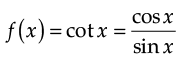
It is discontinuous at
sin x = 0
⇒ x = nπ, n ∈ Z
Thus, the given function is discontinuous at {x = nπ : n ∈ Z}.
Q.7. The set of points where the function f given by f(x) = |2x – 1|sin x is differentiable.
Ans. Given that,
f (x) =| 2x-1| sin x
The function sin x is differentiable.
The function |2x – 1| is differentiable, except
2x – 1 = 0
⇒ x = 1/2
Thus, the given function is differentiable
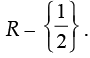
Q.8. Where is the graph of the inequality 2x + 3y > 6 lies?
Ans. Since, the equation 2x + 3y > 6, hence half plane that neither contains the origin nor the points of the line 2x + 3y = 6.
Q.9. The feasible solution for a LPP is shown in given figure. Let Z = 3x – 4y be the objective function. Find the Minimum of Z occurs at what point.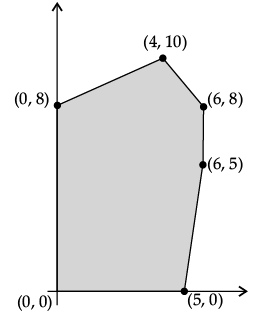
Ans. 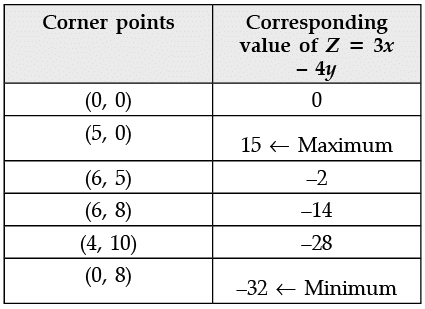
He menicneim, um of Z occurs at (0, 8) and its minimum value is (–32).
Q.10. The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y.
Column A | Column B |
| Maximum of Z | 325 |
Compare the quantity in Column A and Column B.
Ans.
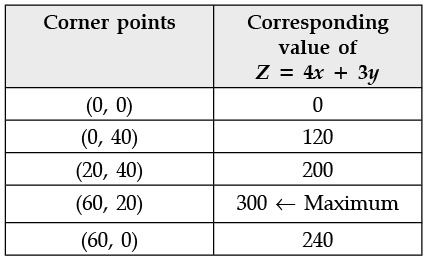
Hence, maximum value of Z = 300 < 325
So, the quantity in column B is greater.
Q.11. What is the domain of the function f : R → R defined by f(x) = 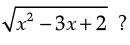
Ans.
Here x2 – 3x + 2 ≥ 0
⇒ (x – 1)(x – 2) ≥ 0
⇒ x ≤ 1 or x ≥ 2
Hence the domain of f = (– ∞, 1] ∪ [2, ∞)
Q.12. If A = {1, 2, 3} and B = {a, b, c, d, e}, then what is the number of injective functions from A to B ?
Ans. Number of one-one functions = 5P3 = 60
Q.13. What is the equation of normal to the curve y = tan x at (0, 0) ?
Ans. y + x = 0
Given that the equation of the curve y = tan x at (0, 0) is x +y= 0 .
∵ y = tan x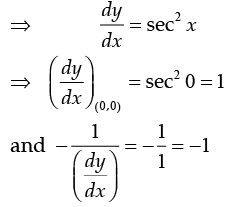
∴ Equation of normal to the curve y = tan x at (0, 0) is
y - 0 = -1(x - 0)
⇒ y+ x = 0
Q.14. What is the integrating factor of x dy/dx - y = x4- 3x ?
Ans. Given that, 
⇒ dy/dx - y/x = x3 - 3
Here, p = -1/x, Q = x3 - 3
∴ 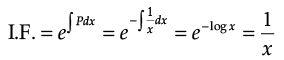
OR
What is the general solution of the differential equation log dy/dx = 2x + y ?
Ans.
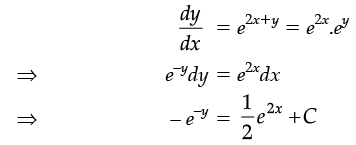
⇒ e2x + 2e–y + 2C = 0
Q.15. Find the area bounded by the curve y = sin x and the x-axis between x = 0 and x = 2p.
Ans.
= 2 + 2 sq. units
= 4 sq. units
Q.16. Evaluate 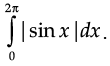
Ans. Let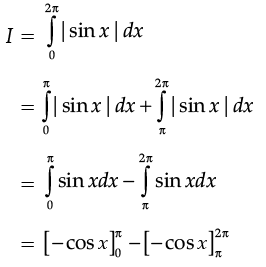
= [–cos π + cos 0] – [–cos 2π + cos π]
= [1 + 1] – [–1 – 1] = 2 + 2 = 4
OR
Find 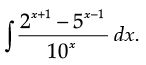
Ans.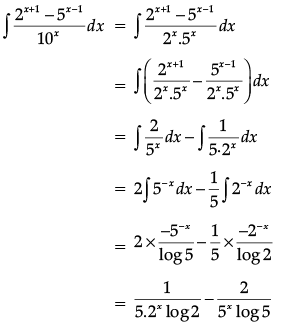
Section - II
Both the case study based questions are compulsory. Attempt any 4 sub parts from each question 17 and 18. Each question carries 1 mark.
Q.17. Let X denote the number of colleges where you will apply after your results and P(X = x) denotes your probability of getting admission is x number of colleges. It is given that: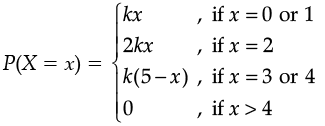
where k is a positive constant.
Then answer the following questions, based on the above information:
(i) What is the sum of all the probabilities of a distribution ?
(a) –1
(b) 0
(c) 1
(d) 2
Ans. c
(ii) What is the value of k ?
(a) 2/9
(b) 3/8
(c) 1/8
(d) 4/9
Ans. c
(iii) Find the probability that you will get admission in exactly one college ?
(a) 2/9
(b) 1/8
(c) 3/8
(d) 4/9
Ans. b
(iv) Find the probability that you will get admission in at most 2 colleges ?
(a) 5/8
(b) 4/9
(c) 17/21
(d) 1/21
Ans. a
(v) Find the probability that you will get admission in at least 2 colleges ?
(a) 2/9
(b) 8/17
(c) 5/9
(d) 7/8
Ans. d
Q.18. Two friends start a game in which both of them have equal chances to throw a pair of dice. Now, they noticed the number of doublets in their game in three throws of a pair of dice. Based on the above information answer the following questions :
(i) The values of p and q are:
(a) 1/2 and 1/2
(b) 1/3 and 2/3
(c) 1/6 and 5/6
(d) 0 and 1
Ans. c
(ii) The value of P(X = 3) is :
(a) 125/216
(b) 75/216
(c) 15/216
(d) 1/216
Ans. d
(iii) The mean of the above information is :
(a) 13
(b) 14
(c) 12
(d) 15
Ans. c
(iv) The variance of the above data is :
(a) 112
(b) 512
(c) 619
(d) 719
Ans. b
(v) The Standard Deviation of the above data is :
(a) √15/6
(b) √15/2
(c) √15/3
(d) √15/4
Ans. a
PART - B
Section - III
Q.19. If A and B are two independent events, then prove that the probability of occurrence of atleast one of A and B is given by 1 – P(A').P(B').
Ans. Required Probability = P(A ∪ B)
= P(A) + P(B) – P(A).P(A)
= P(A)[1 – P(B)] + 1 – P(B')
= P(A)P(B') – P(B') + 1
= [1 – P(B')][1 – P(A)]
= 1 – P(A') P(B')
Q.20. Find the area of the region bounded by the curve y = x + 1 and the lines x = 2 and x = 3.
Ans.
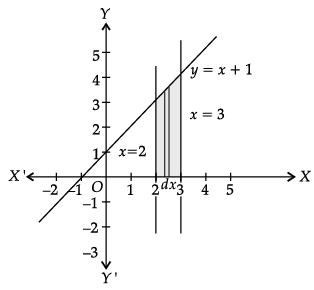
From figure, area of the shaded region,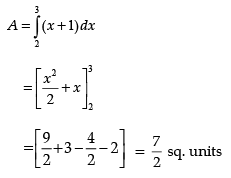
Q.21. Show that the function f in A = R – {2/3} defined as f(x) = 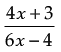 is onto.
is onto.
Ans.
Let, y ∈ B
∴ y = f(x)
or 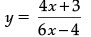
or y(6x – 4) = 4x + 3
or 6xy – 4y = 4x+3
or 6xy – 4x = 4y + 3
or x(6y – 4) = 4y + 3
or 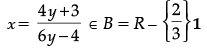
or For every value of y except y = {2/3}, there is
a pre-image x = 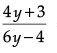 = g(y).
= g(y).
or x ∈ A
∴ f is onto.
OR
How many equivalence relations on the set {1, 2, 3} containing (1, 2) and (2, 1) are there in all ? Justify your answer.
Ans. Equivalence relations could be the following:
{(1, 1), (2, 2), (3, 3), (1, 2), (2, 1)} and
{(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2)}
So, only two equivalence relations.
Q.22. If A = 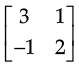 and I =
and I = 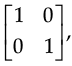 find k so that A2 = 5A + kI.
find k so that A2 = 5A + kI.
Ans.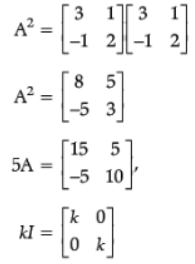
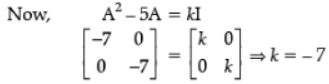
Q.23. Differentiate tan–1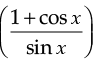 with respect to x.
with respect to x.
Ans. 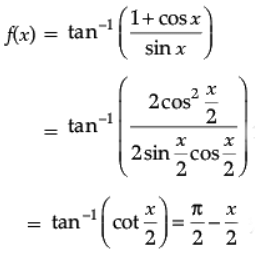
∴ f'(x) = -1/2
OR
Find dy/dx at x = 1, y = π/4 if sin2y + cos xy = K.
Ans.
From the given equation
Q.24. Evaluate 
Ans. 
= – 1 + 2 = 1
Detailed Solution:
Let 
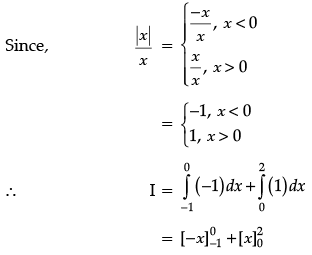
= – [0 – (–1)] + (2 – 0)
= –1 +2 = 1
Q.25. Find 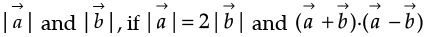 = 12
= 12
Ans.
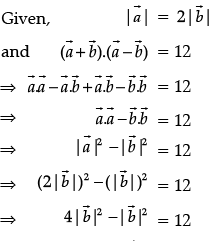
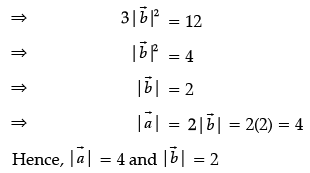
OR
Find the unit vector perpendicular to each of the vectors 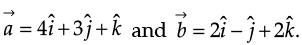
Ans.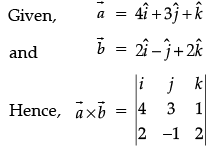
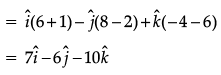
Unit vector perpendicular to each at the vector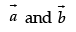

Q.26. Given two independent events A and B such that P(A) = 0.3 and P(B) = 0.6, find P(A' ∩ B').
Ans. P(A'∩B') = P(A∪B)' 1
= 1 – P(A∪B)
= 1 – 0.72 = 0.28
Alternate Method:
P(A'∩B') = P(A').P(B')
= [1 – P(A)] [1 – P(B)] 1
= [1 – 0.3] [1 – 0.6]
= (0.7).(0.4)
⇒ P(A'∩B') = 0.28
Q.27. Check whether the relation R in the set R of real numbers, defined by R = {(a, b) : 1 + ab > 0}, is reflexive, symmetric or transitive.
Ans.
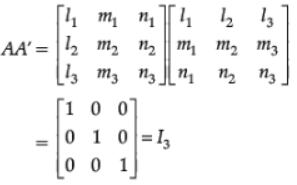
because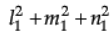 = 1, for each i = 1, 2, 3
= 1, for each i = 1, 2, 3
lilj + mimj + ninj = 0(i ≠ j) for each i, j = 1, 2, 3
Q.28. If y = (log x)x + xlog x, then find dy/dx.
Ans. Let us suppose, y = u + v
where u = [log (x)]x
and v = xlogx ...(ii)
First take u = [log(x)]x
Taking log of both the sides
logu = xloglogx
Now differentiating the above w.r. to x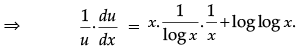
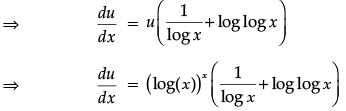
Now take v = xlogx
log v = logx.logx
[Taking log on both sides]
= (log x)2
Differentiating w.r.t. x
⇒ dv/dx = 2xlogx–1.logx ...(v)
equation (i), (iv) and (v)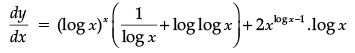
OR
If y = log (1 + 2t2 + t4), x = tan–1t, find d2y/dx2.
Ans. y = log (1 + 2t2 + t4)
y = log (1 + t2)2
y = 2log (1 + t2)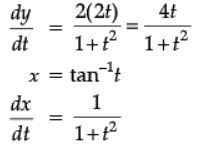
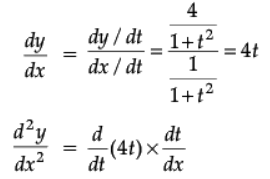
= 4 × (1 + t2) = 4(1 + t2)
Section - IV
Question Numbers 29 to 35 carry 3 marks each.
Q.29. Solve the differential equation x dy/dx + y = x cos x + sin x, given y (π/2) = 1.
Ans.
x dy/dx + y = xcos x + sin x
or dy/dx + 1/x.y = cos x + 1/x sin x
∴ I.F. = 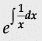 = elog x = x
= elog x = x
∴ Solution is xy = ∫( xcos x + sin x)dx
or xy = xsin x + C
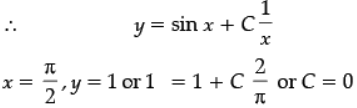
Solution is y = sin x.
Q.30. If A =  Find A–1.
Find A–1.
Hence, solve the system of equations :
3x + 3y + 2z = 1
x + 2y = 4
2x – 3y – z = 5
Ans. 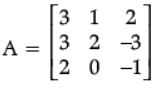
|A| = 3(– 2) – 1(3) + 2(– 4)
= – 6 – 3 – 8 = – 17 ≠ 0
∴ A–1 exists.
(At)X = B
⇒ X = (At)–1B
⇒ X = (A–1)tB [∵ (At)-1 = (A-1)t]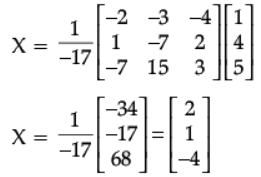
x = 2, y = 1, z = – 4
Q.31. Solve the following L.P.P. graphically:
Minimise Z = 5x + 10y
Subject to x + 2y ≤ 120
Constraints x + y ≥ 60
x – 2y ≥ 0
and x, y ≥ 0
Ans.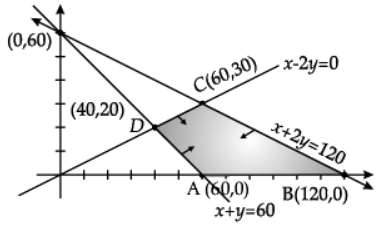
Correct graph of 3 lines
Correct Shade of 3 lines
Z = 5x + 10y
Z|A (60, 0) = 300
Z|B (120, 0) = 600
Z|C (60, 30) = 600
Z|D (40, 20) = 400
Minimum value of Z = 300 at x = 60, y = 0
Q.32. Probability of solving specific problem independently by A and B are 1/2 and 1/3 respectively. If both try to solve the problem, independently, then find the probability that (i) the problem is solved ? (ii) exactly one of them solves the problem ?
Ans.
Let E1: Problem solved by A
E2: Problem solved by B
∴ P(E1) = 1/2 and P(E2) = 1/3
or 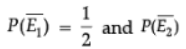 = 2/3
= 2/3
P(E1 ∩ E2) = P(E1).P(E2) = 1/2, 1/3 = 1/6
(i) P(Problem is solved)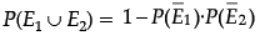
= 1 - 1/2 x 2/3 = 2/3
(ii) P(one of them is solved)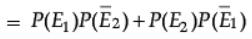
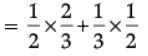
= 1/2
OR
Three persons A, B and C apply for a job of Manager in a Private company. Chance of their selection (A, B and C) are in the ratio 1 : 2 : 4. The probability that A, B and C can introduce changes to improve profits of company are 0·8, 0·5 and 0·3 respectively, if the changes does not take place, find the probability that it is due to the appointment of C.
Ans.
Let the events be described as below :
A : No change takes place
E1 : Person A gets appointed
E2 : Person B gets appointed
E3 : Person C gets appointed
The chances of selection of A, B and C are in the ratio 1 : 2 : 4.
Hence,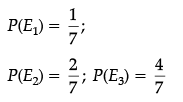
Probabilities of A, B and C introducing changes to improve profits of company are 0·8, 0·5 and 0·3 respectively.
Hence probability of no changes on appointment of A, B and C are 0·2, 0·5 and 0·7 respectively.
Hence,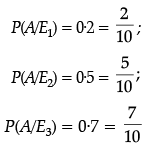
Therefore, required probability i.e., (E3/A) is P(E3/A)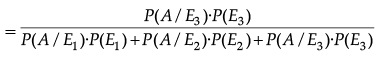
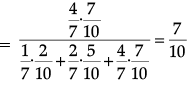
∴ If no change takes place, the probability that it is due to appointment of C is 7/10.
Q.33. If y = xsinx + sin(xx), find dy/dx.
Ans. Let u = xsinx
⇒ ln u = sin x ln x
⇒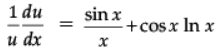
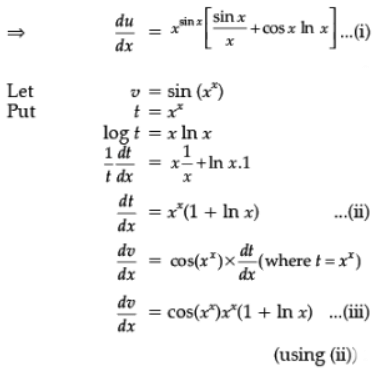
Since, y = u + v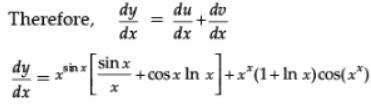
Q.34. If x = a sin pt, y = b cos pt, then find dy/dx at t = 0.
Ans. Given x = a sin pt
∴ dx/dt = ap cos pt
and y = b cos pt
∴ dy/dt = – bp sin pt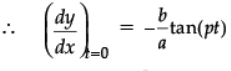
= 0
OR
If y = Peax + Qebx, show that 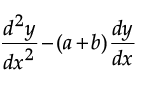 + aby = 0.
+ aby = 0.
Ans. y = Peax + Qebx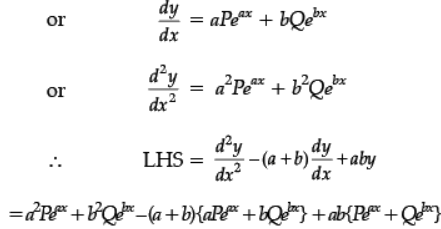
= Peax {a2 – a2 – ab + ab} + Qebx{b2 – ab – b2 + ab}
= 0 + 0 = 0 = RHS
Q.35. Find: 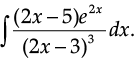
Ans. Let 2x = t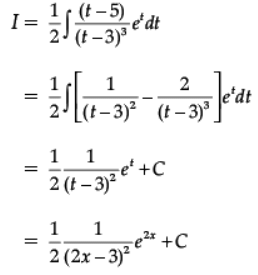
Section - V
Question numbers 36 to 38 carry 5 marks each.
Q.36. Find the point on the curve y2 = 4x which is nearest to the point (2, 1).
Ans. Suppose the required point on the curve is K(p, q) and the given point is A(2, 1).
∴ q2 = 4p
To find nearest point let us suppose S2 = T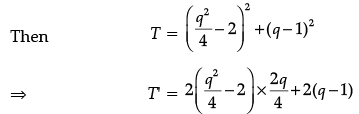
For critical points T' = 0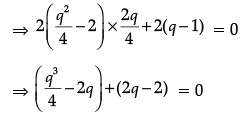
⇒ q3 = 8
⇒ q = 2
To find the maxima or minima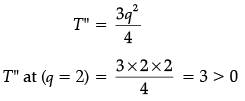
Therefore, T is least
From (i) q2 = 4p
⇒ 22 = 4p
⇒ p = 1
Therefore, the required point is K(1, 2).
OR
If xcos (a + y) = cos y, then prove that dy/dx = 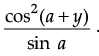 Hence, show that
Hence, show that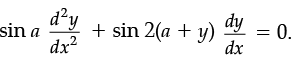
Ans. Given, xcos (a + y) = cos y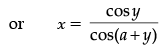
On differentiating both sides w.r.t. y, we get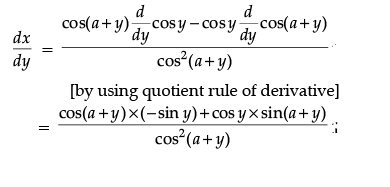
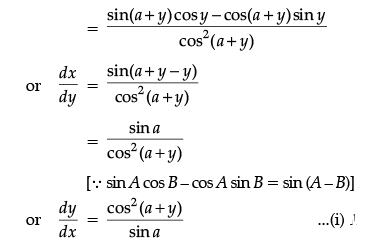
Again, on differentiating both sides of Eq. (i) w.r.t. x, we get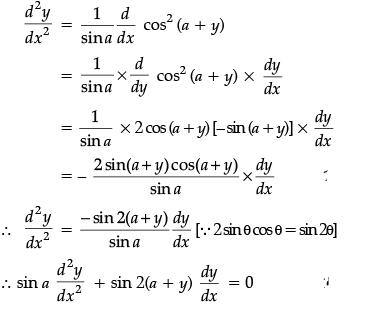
Hence Proved.
Q.37. Find the position vector of foot of perpendicular and the perpendicular distance from the point P with position vector 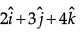 to the plane
to the plane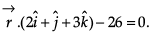 Also find the image of P in the plane.
Also find the image of P in the plane.
Ans. Equation of plane : 2x + y + 3z = 26
Normal to the plane = 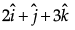
∴ < 2, 1, 3 > are direction ratios of the normal to the plane.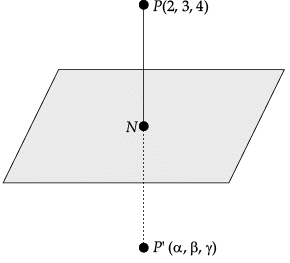
Equation of the line through P(2, 3, 4) and perpendicular to the given plane is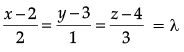
∴ Co-ordinates of point N are
N(2λ + 2, λ + 3, 3λ + 4)
Since N lie s on the plane,
∴ 2(2λ + 2) + (λ + 3) + 3(3λ + 4) = 26
4λ + 4 + λ + 3 + 9λ + 12 = 26
or 14λ = 26 – 19
or 14λ = 7
or λ = 1/2
∴ Co-ordinates of the foot of the perpendicular i.e., N are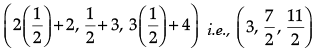
∴ The length of perpendicular from P to given plane is
Now, N is the mid-point of PP’, where P’(α, β, γ) is the image of point P.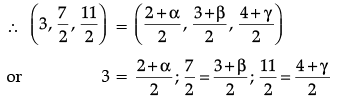
or 6 = 2 + α; 7 = 3 + β; 11 = 4 + γ
or α = 4; β = 4; γ = 7
∴ Image of point P is P’(4, 4, 7).
OR
Find the equation of the plane through the line 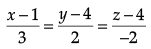 and parallel to the line
and parallel to the line 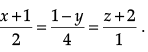 Hence, find the shortest distance between the lines.
Hence, find the shortest distance between the lines.
Ans. The two given lines are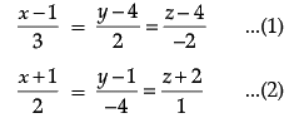
Let a, b, c the D.R's of the normal to the plane containing the line (1).
Therefore, equation of plane is
a(x – 1) + b(y – 4) + c(z – 4) = 0 ...(3)
3a + 2b – 2c = 0 ...(4)
(Q Required plane contains line (1))
2a - 4b + 1c = 0 ...(5)
(Q line (2) is parallel to the required plane)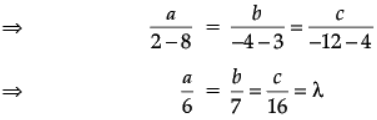
Putting, a = 6λ, b = 7λ, c = 16λ in (3), we get
⇒ 6λ(x – 1) + 7λ(y – 4) + 16λ(z – 4) = 0
⇒ 6x + 7y + 16z – 98 = 0, which is the required equation of the plane
Since line (2) is parallel to required plane
∴ SD between two lines = Perpendicular distance of the point (–1, 1 –2) from the plane.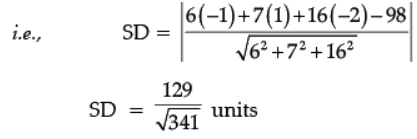
Q. 38. If A = 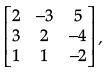 Find A–1. Use it to solve the system of equations
Find A–1. Use it to solve the system of equations
Hence, solve the system of equations :
2x – 3y + 5z = 11
3x + 2y – 4z = – 5
x + y – 2z = – 3
Ans.
|A| = – 1 ≠ 0 ∴ A–1 exists
Co-factors of A are :
A11 = 0; A12 = 2; A13 = 1 1 m for
A21 = – 1; A22 = – 9; A23 = – 5 4 correct
A31 = 2; A32 = 23; A33 = 13 Co-factors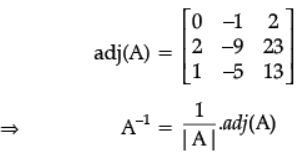
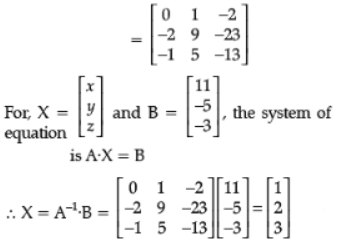
∴ x = 1, y = 2, z = 3
OR
Show that the matrix BT AB is symmetric or skew-symmetric accordingly when A is symmetric or skewsymmetric.
Ans. Case I : Let A be a symmetric matrix. Then AT = A.
Now (BT AB)T = BTAT(BT)T [By reversal law]
= BTATB [∵ (BT)T = B]
or (BTAB)T = BTAB [∵ AT = A]
∴ BT AB is a symmetric matrix.
Case II : Let A be a skew-symmetric matrix.
Then, AT = – A.
Now (BT AB)T = BTAT(BT)T [By reversal law]
or (BTAB)T = BTATB [∵ (BT)T = B]
or (BTAB)T = BT(- A)B [∵ AT = - A]
or (BTAB)T = - BTAB
∴ BT AB is a skew-symmetric matrix.
|
203 videos|307 docs|139 tests
|
FAQs on Mathematics: CBSE Sample Question Paper (2020-21)- 1 - Mathematics (Maths) Class 12 - JEE
| 1. What is the format of the CBSE Sample Question Paper for Mathematics (2020-21)? |  |
| 2. How many sections are there in Part A of the CBSE Sample Question Paper for Mathematics (2020-21)? |  |
| 3. What are the sections included in Part B of the CBSE Sample Question Paper for Mathematics (2020-21)? |  |
| 4. Is there any difference in the complexity level between Part A and Part B of the CBSE Sample Question Paper for Mathematics (2020-21)? |  |
| 5. How many questions are there in each section of the CBSE Sample Question Paper for Mathematics (2020-21)? |  |















