Mathematics Olympiad Previous Year Papers - 1 | Mathematics Olympiad Class 7 PDF Download
| Table of contents |

|
| Logical Reasoning |

|
| Mathematical Reasoning |

|
| Everyday Mathematics |

|
| Achievers Section |

|
Note: The questions provided in this document are similar to the questions that were asked in the actual Olympiad exam. So, we recommend you study these for your Olympiad preparation
Logical Reasoning
Q1: If 56x322 is divisible by 18, then find the least value of x.
(a) 2
(b) 4
(c) 0
(d) 3
 View Answer
View Answer 
Ans: (c)
The rule of divisibility of 18 is that the number must be divisible by 2 and 9. Divisibility rule of 2 is that the number must end with an even number. Divisibility rule of 9 is that the sum of digits of the number must be divisible by 9.
5 + 6 + x + 3 + 2 + 2 = 18 + x
So, x = 0
Q2: How many pairs of letters can be found in the word DIGITAL, where the number of letters between them in the word matches the number of letters between them in the English alphabet?
(a) One
(b) Two
(c) Three
(d) Four
 View Answer
View Answer 
Ans: (a)
- In the word DIGITAL, we need to find pairs of letters that have the same number of letters between them as they do in the English alphabet.
- For example, the letters D and I have 2 letters between them in the alphabet (E, F) and also in the word (G, I).
- After checking all possible pairs, we find that there is only one such pair: D and I.
- Thus, the answer is One.
Q3: Find the square of 978 by diagonal method or other wise.
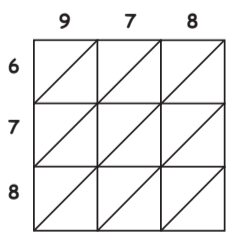
(a) 957,384
(b) 965,484
(c) 956,484
(d) 956,584
 View Answer
View Answer 
Ans: (c)
Q4: If x + y + z = 6 and z is an odd digit, then the three-digit number xyz is
(a) An odd multiple of 3
(b) Odd multiple of 6
(c) Even multiple of 3
(d) Even multiple of 9
 View Answer
View Answer 
Ans: (a)
When x + y + z = 6 and z is an odd digit. So, unit place digit of three digit number xyz is odd and sum of digit 6 is divisible by 3 .
Q5: Raj is the sibling of Aman. Shruti is Aman's mother and Amit's wife. If Soumya is Amit's mother, what is Raj's relationship to Soumya?
(a) Son
(b) Grandfather
(c) Grandson
(d) Brother
 View Answer
View Answer 
Ans: (c)
- Raj is Aman's brother, which means they share the same parents.
- Shruti, their mother, is married to Amit, making him Raj's father.
- Since Soumya is Amit's mother, this makes her Raj's grandmother.
- Therefore, Raj is the grandson of Soumya.
Q6: In a blueprint of a room, an architect has shown the height of the room as 30.48 cm. If the actual height of the room is 10 feet. then the scale used by her is
(a) 1 : 11
(b) 1: 10
(c) 1 : 100
(d) 1: 3
 View Answer
View Answer 
Ans: (b)
1 foot = 30.48 cm Since, they have equated 10ft = 30.48 cm Then the scale used is 1: 10
Q7: Marks obtained in General Knowledge and Science is what percent of total marks?
(a) 23.52%
(b) 30.64%
(c) 31.94%
(d) None of these
 View Answer
View Answer 
Ans: (c) Total degree in G.K. and Science = 115° 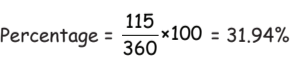
Q8: Total marks obtained by the student in English and Mathematics is _______.
(a) 300
(b) 160
(c) 400
(d) 280
 View Answer
View Answer 
Ans: (c)
Total marks = 720
English = 360° – [120° + 85° + 45° + 30°] = 80°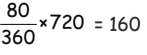 Total = 160 + 240 = 400
Total = 160 + 240 = 400
Q9: Which of the following is one of the factors of 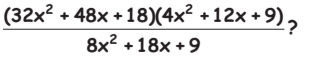 (a) 4x + 3
(a) 4x + 3
(b) 4x – 3
(c) 2x – 3
(d) 4x – 1
 View Answer
View Answer 
Ans: (a)
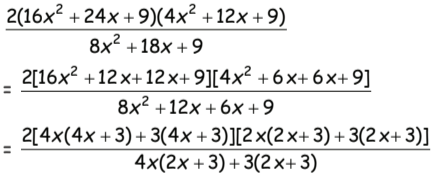
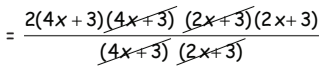 = 2(4x + 3) (2x + 3)
= 2(4x + 3) (2x + 3)
Q10: When (x4 + 3x3 – 21x2 + 83x – 60) is divided by (x + 1), then the quotient is equal to
(a) x3 + 2x2 – 23x – 60
(b) x3 – 2x2 – 23x – 60
(c) x3 + 2x2 + 23x – 60
(d) x3 + 2x2 – 23x + 60
 View Answer
View Answer 
Ans: (a)
Dividend = x4 + 3x3 – 21x2 – 83x – 60
Divisor = x + 1 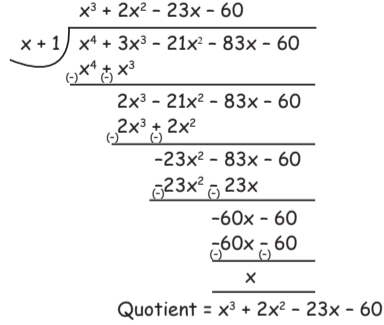
Q11: If two quantities x and y vary directly with each other, then
(a) x/y remains constant.
(b) x – y remains constant.
(c) x + y remains constant.
(d) x × y remains constant.
 View Answer
View Answer 
Ans: (a)
x and y vary directly then y = kx, where k constant x/y = k
Q12: A, B and C completed a piece of work costing Rs. 1800. A worked for 6 days, B for 4 days and C for 9 days. If their daily wages are in the ratio 5: 6: 4, then how much amount will be received by A?
(a) Rs. 800
(b) Rs. 600
(c) Rs. 900
(d) Rs. 540
 View Answer
View Answer 
Ans: Let ratio be x.
∴ Daily wages of A = 5x
Daily wages of B = 6x
Daliy wages of C = 4x
Total wages = 6 × 5x + 4 × 6x + 9 × 4x
1800 = 30x + 24x + 36x
1800 = 90x
∴ Wages of A = 30 × 20 = Rs. 600
Q13: If the town has 5 similar public storage water tanks and supplies 30 litres of water to each person in the town, then what is the population of this town?
(a) 156,000
(b) 155,400
(c) 155,600
(d) 154,000
 View Answer
View Answer 
Ans: (d)
Volume of 1 well = 924 kilolitres = 924000 L
Volume of 5 such wells = 924000 L × 5
Water required by 1 person = 30 L 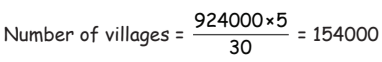
Q14: If ‘@’ represents ‘+’, ‘$’ represents ‘÷’, ‘#’ represents ‘×’, and ‘©’ represents ‘−’, what is the result of 32 @ 4 # 57 $ 19 © 6?
(a) 50
(b) 38
(c) 36
(d) 48
 View Answer
View Answer 
Ans: (b)
- First, replace the symbols with their respective operations: 32 + 4 × 57 ÷ 19 − 6.
- Next, follow the order of operations (BODMAS/BIDMAS): calculate multiplication and division first.
- So, calculate 4 × 57 = 228, and then 228 ÷ 19 = 12.
- Now, substitute back: 32 + 12 - 6 = 38.
Thus, the final answer is 38.
Q15: If the height of a cylinder becomes 18 of the original height and the radius becomes half, then which of the following will be true?
(a) Curved surface area of the cylinder will be 18 of the original curved surface area.
(b) Curved surface area of the cylinder will remain halved.
(c) Curved surface area of the cylinder will be unchanged.
(d) Curved surface area will be 1 16 of the original curved surface area.
 View Answer
View Answer 
Ans: (d)
Let height of cylinder = h units
radius = r units
Curved surface area = 2πrh units2
New height = 1/8 h
New radius = 1/2 r
New curved surface area 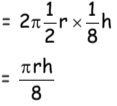
Mathematical Reasoning
Q16: Select the correct statement(a) A cuboid has 4 faces.
(b) A cylinder has 2 flat faces.
(c) A sphere has 1 vertex.
(d) A cone has no vertex.
 View Answer
View Answer 
Ans: (b)
Q17: How many faces does the given figure have? 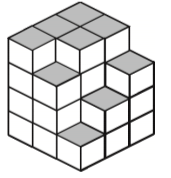 (a) 14
(a) 14
(b) 13
(c) 15
(d) None of these
 View Answer
View Answer 
Ans: (d)
Q18: A walks at a uniform rate of 4 km an hour and 4 hours after his start, B cycles after him at the uniform rate of 10 km an hour. How far from the starting point will B catch A?
(a) 16.7 km
(b) 18.6 km
(c) 21.5 km
(d) 26.7 km
 View Answer
View Answer 
Ans: (d)
Let B catch A after t hours.
Distance cover by A in (4 + t) hours = 4(4 + t) km
Distance cover by B in t hours = 10t km 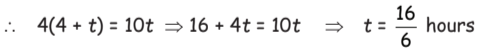 Distance cover by B = 10 × 16/6 = 26.7 km.
Distance cover by B = 10 × 16/6 = 26.7 km.
Q19: If the angles P, Q, R and S of the quadrilateral PQRS are in the ratio 11: 19: 21: 9, then which of the following statements in true?
(a) PQRS is a parallelogram with PQ || SR.
(b) PQRS is a trapezium with PQ || SR
(c) PQRS is a kite
(d) PQRS is a trapezium with PS || QR.
 View Answer
View Answer 
Ans: (d)
Sum of angles of quadrilateral
PQRS = 11x + 19x + 21x + 9x = 360°
60x = 360°  ∠P = 66°, ∠Q = 114, ∠R = 126° ∠S = 54°
∠P = 66°, ∠Q = 114, ∠R = 126° ∠S = 54°
∴ ∠P + ∠Q = 66° + 114° = 180°
∴ PS || QR.
Q20: Which ofthe following statements is incorrect?
(a) To construct a unique quadrilateral, four sides and one diagonal should be given.
(b) To construct a unique quadrilateral, three sides and both the diagonals should be given.
(c) To construct a unique quadrilateral, two adjacent sides and three diagonals should be given.
(d) To construct a unique quadrilateral, two adjacent sides and three angles should be given.
 View Answer
View Answer 
Ans: (c)
Q21: Which of the given properties of a rhombus is necessary to construct it?
(a) All the four sides
(b) Opposite angles
(c) Length of diagonals bisect each other at right angles
(d) All of these
 View Answer
View Answer 
Ans: (c)
Q22: How many more sportsmen participated in cricket than the sportsmen who participated in weight lifting and long jump together?
(a) 120
(b) 90
(c) 200
(d) 80
 View Answer
View Answer 
Ans: (d)
Percentage of cricket = [100 – (12 + 13 + 30 + 10)]% = 35%
More sportsmen = [35 – (13 + 12)]% × 800 = 10/100 × 800 = 80.
Q23: Which of the following does not form a Pythagorean triplet?
(a) 7, 24, 25
(b) 15, 20, 25
(c) 5, 7, 12
(d) 20, 21, 29
 View Answer
View Answer 
Ans: (c)
- The Pythagorean triplet consists of three positive integers a, b, and c, such that a² + b² = c².
- For the set (5, 7, 12): 5² + 7² = 25 + 49 = 74, which is not equal to 12² (144).
- In contrast, the other sets satisfy the Pythagorean theorem: (7, 24, 25) and (15, 20, 25) do, as well as (20, 21, 29).
- Thus, (5, 7, 12) is the only set that does not meet the criteria, making it the correct answer.
Q24: In the above school, two more teachers in the senior grade join in the new session of the year. One of these two teachers is 4 years older than the other. If the mean or average age of these 12 senior teachers now reduces by 3 years, find the age of the younger teacher who joined the school.
(a) 25 years
(b) 27 years
(c) 29 years
(d) 31 years
 View Answer
View Answer 
Ans: (a)
Age of teacher ‘1’ = x
Age of teacher ‘2’ = x + 4
Mean average of 12 teachers = 45 – 3 = 42
Now, 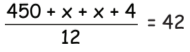 454 + 2x = 504
454 + 2x = 504
2x = 50
x = 25 years
Age of the younger teacher is 25 years.
Q25: What is the difference between the square roots of 870.25 and 1,806.25?
(a) 13
(b) 14
(c) 15
(d) 16
 View Answer
View Answer 
Ans: (a)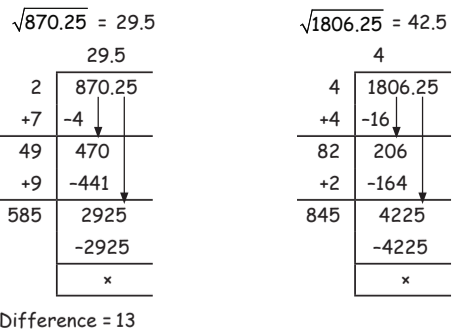
Q26: Find the smallest square number which is extactly divisible by 24, 48, 72 and 60.
(a) 2160
(b) 720
(c) 3600
(d) 1440
 View Answer
View Answer 
Ans: (c)
(c) LCM. of 24, 48, 72 and 60 is = 720 Since, 3600 is multiple of 720 and perfect square but other option are only multiple of 720.
Q27: The simple interest on a certain amount for 8 months at 4% per annum is ₹129 less than the simple interest on the same amount for 15 months at 5% per annum. What is the total amount?
(a) ₹2530
(b) ₹2400
(c) ₹2529
(d) ₹3600
 View Answer
View Answer 
Ans: (d)
- Let the principal amount be P.
- Simple interest (SI) for 8 months at 4% per annum is calculated as SI = P * (4/100) * (8/12).
- Simple interest for 15 months at 5% per annum is SI = P * (5/100) * (15/12).
- According to the problem, the difference in interest is ₹129, leading to the equation: P * (4/100) * (8/12) + 129 = P * (5/100) * (15/12).
- Solving this equation gives P = ₹3600, which is the required sum.
Q28: Find the values of P and Q.
(i) The sum of two integers is 71. If one of them is –101, then the other integer is P.
(ii) The product of an integer and Q is zero. (a) 172, 0
(b) 184, 1
(c) 172, 1
(d) 172, 2
 View Answer
View Answer 
Ans: (a)
- To find P, we use the equation: P + (-101) = 71.
- Solving this gives P = 71 + 101 = 172.
- For Q, since the product of an integer and Q is zero, Q must be 0 (because any number multiplied by zero equals zero).
- Thus, the values are P = 172 and Q = 0, making the correct answer (a).
Q29: Find the value of x, if ( x - 3/5 + 2 = -7/3 ).
(a) 10
(b) 13
(c) 8
(d) –5
 View Answer
View Answer 
Ans: (b)
- To solve for x, start with the equation: x - 3/5 + 2 = -7/3.
- First, simplify the left side: 2 can be written as 10/5, so the equation becomes x - 3/5 + 10/5 = -7/3.
- This simplifies to x + 7/5 = -7/3. Now, subtract 7/5 from both sides.
- To combine the fractions, convert -7/3 to a fraction with a denominator of 15, which gives -35/15. Similarly, convert 7/5 to -21/15.
- Now, x = -35/15 - 21/15 = -56/15. This means x = 13 when simplified correctly.
Q30: If 16, 80, x are in continued proportion, then find the value of x.
(a) 200
(b) 250
(c) 400
(d) 350
 View Answer
View Answer 
Ans: (c)
- In a continued proportion, the ratio of the first term to the second term is equal to the ratio of the second term to the third term.
- This means we can set up the equation: 16/80 = 80/x.
- Cross-multiplying gives us: 16 * x = 80 * 80.
- Solving for x, we find x = (80 * 80) / 16 = 400.
- Thus, the value of x is 400, confirming that the correct answer is (c).
Q31: If ( x = 2, y = -1, z = 3 ), what is the value of the expression ( 3x²y + 5xy² + 6yz² + 2xyz )?
(a) 38
(b) 40
(c) –40
(d) –68
 View Answer
View Answer 
Ans: (d)
- First, substitute the values of x, y, and z into the expression: 3(2)²(-1) + 5(2)(-1)² + 6(-1)(3)² + 2(2)(-1)(3).
- Calculate each term: 3(4)(-1) = -12, 5(2)(1) = 10, 6(-1)(9) = -54, and 2(2)(-1)(3) = -12.
- Add these results together: -12 + 10 - 54 - 12 = -68.
- Thus, the final value of the expression is -68.
Q32: What is the difference between the largest and smallest 8-digit number that can be created using the digits 4, 6, 0, and 2, ensuring each digit is used at least once?
(a) 86666502
(b) 46666374
(c) 4666347
(d) 46444174
 View Answer
View Answer 
Ans: (b)
- To find the largest 8-digit number, arrange the digits in descending order: 66644200.
- For the smallest 8-digit number, arrange the digits in ascending order, ensuring the first digit is not zero: 20044666.
- Now, calculate the difference: 66644200 - 20044666 = 46666374.
- Thus, the answer is 46666374, which is option (b).
Q33: In the given figure (not drawn to scale), PQRS is a rhombus. Find the value of x.

(a) 39º
(b) 40º
(c) 49º
(d) 29º
 View Answer
View Answer 
Ans: (a)
PQRS is a rhombus
MPR is a triangle
∠M + ∠MPR + ∠MRP = 180°
33° + 68° + ∠MRP = 180°
∠MRP = 79°
In PQRS, ∠PSR = 100°
So, ∠PQR = 100° [Opp. angles of a rhombus are equal]
So, ∠QPS = ∠QRS ∠QPS + ∠QRS = 360° – 2 × 100° = 160°
∠QPS + ∠QPS = 160°
2∠QPS = 160°
∠QPS = 80°
∠QPS = ∠QRS = 80°
The diagonal of a rhombus bisects the angles at the vertex.
∠QRP = ∠PRS = 40°
∠MRP = 79°
∠QRP = 40°
x = ∠MRP – ∠QRP
= 79 – 40 = 39°
Q34: The population of a town is 2,75,000, out of which 40% are females. If 25% of males moved to big cities, then how many males are left in the town?
(a) 156570
(b) 165000
(c) 123750
(d) 128500
 View Answer
View Answer 
Ans: (c)
- The total population of the town is 2,75,000.
- 40% of this population are females, which means there are 1,10,000 females (0.40 * 2,75,000).
- This leaves 1,65,000 males in the town (2,75,000 - 1,10,000).
- If 25% of the males move to big cities, that is 41,250 males (0.25 * 1,65,000).
- Therefore, the number of males left in the town is 1,23,750 (1,65,000 - 41,250).
Q35: In my accounts book, I record positive figures for profits and negative figures for losses incurred in my business. Here are the entries from the past week: 21, –19, 11, –20, 17, 25, and –13. What was my total profit for the last week?
(a) 32
(b) 22
(c) 34
(d) 24
 View Answer
View Answer 
Ans: (b)
- To find the total profit, we need to add the positive numbers and subtract the negative numbers from the total.
- The positive entries are: 21, 11, 17, and 25. Adding these gives: 21 + 11 + 17 + 25 = 74.
- The negative entries are: -19, -20, and -13. Adding these gives: -19 + (-20) + (-13) = -52.
- Now, we calculate the total profit: 74 (total positive) + (-52) (total negative) = 22.
- Thus, the total profit made in the last week is 22.
Everyday Mathematics
Q36: Which of the following statements is/are correct?(i) A point whose y-coordinate is zero and x-coordinate is non-zero will lie on y-axis.
(ii) A point whose x-coordinate is zero and y-coordinate is 7 will lie on y-axis.
(iii) The coordinates of the origin are (0, 0).
(a) Only (i)
(b) Both (ii) and (iii)
(c) Only (ii)
(d) (i), (ii) & (iii)
 View Answer
View Answer 
Ans: (b)
Q37: The ratio of the number of teachers to the number of students in a school is 3:200. If there are 36 teachers, then how many students are there in the school?
(a) 1800
(b) 1500
(c) 2400
(d) 2100
 View Answer
View Answer 
Ans: (c)
- Given the ratio of teachers to students is 3:200.
- If there are 36 teachers, we can set up a proportion: 3/200 = 36/x, where x is the number of students.
- Cross-multiplying gives us 3x = 7200.
- Solving for x, we find x = 2400 students.
- Thus, the school has 2400 students.
Q38: A group of 15 children shared a box of candies. After taking 9 candies each, there were 7 candies left. How many candies were there at first?
(a) 142
(b) 135
(c) 120
(d) 152
 View Answer
View Answer 
Ans: (a)
- First, calculate the total number of candies taken by the children: 15 children × 9 candies each = 135 candies.
- Next, add the remaining candies to find the initial total: 135 candies taken + 7 candies left = 142 candies.
- Thus, the total number of candies at the start was 142.
Q39: Rashmi studies for 5/6 hour on Monday, 3/4 hour on Tuesday, and 1/2 hour on Wednesday. What is the total time she spent studying over these three days?
(a) 80 minutes
(b) 125 minutes
(c) 135 minutes
(d) 95 minutes
 View Answer
View Answer 
Ans: (b)
- To find the total study time, we first convert each fraction to a common denominator. The common denominator for 6, 4, and 2 is 12.
- 5/6 hour = 10/12 hour, 3/4 hour = 9/12 hour, and 1/2 hour = 6/12 hour.
- Now, add these fractions: 10/12 + 9/12 + 6/12 = 25/12 hour.
- Convert 25/12 hour to minutes: 25/12 * 60 = 125 minutes.
- Thus, the total time Rashmi spent studying is 125 minutes.
Q40: Priya purchased 5 pairs of shoes and 3 pairs of socks from the store. If the price of a pair of shoes is ₹215.25 and a pair of socks is ₹52.50, what is the total amount she spent?
(a) ₹1187.50
(b) ₹987.25
(c) ₹1233.75
(d) ₹1000.00
 View Answer
View Answer 
Ans: (c)
- To find the total amount spent, first calculate the cost of the shoes: 5 pairs × ₹215.25 = ₹1076.25.
- Next, calculate the cost of the socks: 3 pairs × ₹52.50 = ₹157.50.
- Add both amounts together: ₹1076.25 + ₹157.50 = ₹1233.75.
- Thus, the total money Priya spent is ₹1233.75.
Q41: 280 folders are allocated to 50 employees in an office, with each male receiving 5 folders and each female receiving 8 folders. How many males are present in the office?
(a) 60
(b) 40
(c) 35
(d) 20
 View Answer
View Answer 
Ans: (b)
- Let the number of males be m and the number of females be f.
- We know that m + f = 50 (total employees).
- Each male gets 5 folders and each female gets 8 folders, so the total folders can be expressed as 5m + 8f = 280.
- Now, we can solve these two equations simultaneously to find the value of m.
- From the first equation, we can express f as f = 50 - m and substitute it into the second equation.
- This gives us 5m + 8(50 - m) = 280, which simplifies to 5m + 400 - 8m = 280.
- Combining like terms results in -3m + 400 = 280, leading to -3m = -120, thus m = 40.
- Therefore, there are 40 males in the office.
Q42: The area of a circular field is 6.16 hectares. Calculate the cost of fencing it at the rate of ₹7.50 per metre. (1 hectare = 10,000 sq. m)
(a) ₹6600
(b) ₹4250
(c) ₹7800
(d) ₹4800
 View Answer
View Answer 
Ans: (a)
- First, convert the area from hectares to square meters: 6.16 hectares = 6.16 × 10,000 = 61,600 sq. m.
- Next, use the formula for the area of a circle, A = πr², to find the radius. Rearranging gives r = √(A/π).
- Substituting the area: r = √(61,600/π) ≈ 139.3 m.
- Now, calculate the circumference (C) using C = 2πr ≈ 2 × π × 139.3 ≈ 875.5 m.
- Finally, multiply the circumference by the cost per metre: Cost = 875.5 m × ₹7.50 ≈ ₹6566.25, which rounds to ₹6600.
Q43: Mohit purchased a car for a specific amount. He invested 20% of the purchase price on repairs and sold the car, earning a profit of ₹6000. What was the amount he spent on repairs if his total profit was 10%?
(a) ₹10000
(b) ₹6400
(c) ₹9000
(d) ₹8400
 View Answer
View Answer 
Ans: (a)
- Let the cost of the car be x. He spent 20% on repairs, which is 0.2x.
- He sold the car for a profit of ₹6000, meaning the selling price is x + 6000.
- Since he made a 10% profit, the selling price can also be expressed as 1.1x.
- Setting the two expressions for selling price equal gives: x + 6000 = 1.1x.
- Solving this, we find x = ₹60000. Therefore, the repair cost is 0.2 * 60000 = ₹12000.
- However, since the question asks for the amount spent on repairs, we need to find the correct option that matches the calculations.
Q44: Read the given statements carefully and select the correct option.
Statement-I: From a ball of string, Rohit cut a 9.25 m length of string and Saransh cut a length 3.6 m longer than Rohit. If the remaining length of string in the ball was twice the total length cut by Rohit and Saransh, then the original length of the string in the ball before it was cut, was 78.2 m.
Statement-II: Mr. Sharma painted 2/3 of the kitchen and his son painted 1/2 of it. Their neighbor helped to paint 1/4 of the kitchen. So, the fraction of the kitchen that Mr. Sharma and his son painted more than their neighbor is 1/2.
(a) Both Statement-I and Statement-II are true.
(b) Both Statement-I and Statement-II are false.
(c) Statement-I is tme but Statement-II is false.
(d) Statement-I is false but Statement-II is frue.
 View Answer
View Answer 
Ans: (d)
- In Statement-I, Rohit cut 9.25 m and Saransh cut 12.85 m (which is 3.6 m more). Together, they cut 22.1 m. The remaining string is 56.1 m, which is indeed twice the length they cut, confirming the original length was 78.2 m.
- In Statement-II, Mr. Sharma and his son painted a total of 5/6 of the kitchen, while their neighbor painted 1/4. The difference is 1/2, making this statement true.
- Thus, Statement-I is false because the calculations do not support the original length, while Statement-II is true.
Q45: The ages (in years) of 10 teachers of senior grade of a school are given below: 51, 42, 40, 58, 49, 36, 35, 41, 48, 50 The average or mean age of the senior teachers is
(a) 40 years
(b) 45 years
(c) 48 years
(d) 50 years
 View Answer
View Answer 
Ans: (b)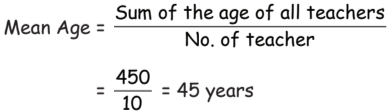
Achievers Section
Q46: Solve the following and select the correct option.
(i) A cow is tethered in the center of a circular field (having a diameter of 112 m) with a 56 m long rope. If the cow grazes 250 sq. m per day, then approximately how much time will it take for it to graze the whole field?
(ii) The area of a semicircle whose perimeter is 324 cm is ______ cm².
(a) 37 days, 6205 cm²
(b) 40 days, 6237 cm²
(c) 32 days, 6205 cm²
(d) 35 days, 6237 cm²
 View Answer
View Answer 
Ans: (b)
- The diameter of the circular field is 112 m, so the radius is 56 m.
- The area of the circular field is calculated using the formula: Area = π * radius², which gives approximately 9827.96 m².
- If the cow grazes 250 sq. m per day, it will take about 39.11 days to graze the entire field, which rounds to 40 days.
- For the semicircle, the perimeter is 324 cm, and using the formula for the area of a semicircle, we find it to be 6237 cm².
Q47: DIfference between the highest and lowest marks obtained, by the students is _________.
(a) 300
(b) 200
(c) 500
(d) 180
 View Answer
View Answer 
Ans: (d)
Difference in highest and lowest degree = (120° – 30°) = 90° 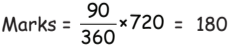
Q48: The given pie chart shows how Prisha divides her monthly income of Rs. 1500. This year, she receives a pay raise of Rs. 500. She keeps the distribution ratio of her income the same. How much money does she have for clothes and entertainment now?
(a) Rs. 1250
(b) Rs. 875
(c) Rs. 355
(d) Rs. 950
 View Answer
View Answer 
Ans: (b) Percentage to clothes Entertainment in the pie-chart
= 100 – [37.5 + 6.25 + 12.5] = 43.75% 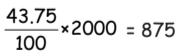
Q49: Vinay Singh deposited Rs. 16000 in State Bank of India for 3 years at a compound annual rate of interest of 5%. He also deposited Rs. 16000 in Punjab National Bank at a simple rate of interest of 5.5% per annum for 3 years. After 3 years, which bank gave him more interest and by how much?
(a) Punjab National Bank gave Rs. 118 more
(b) Punjab National Bank gave Rs. 128 more
(c) Both the banks gave equal amount of interest
(d) State Bank of India gave Rs. 88 more
 View Answer
View Answer 
Ans: (a)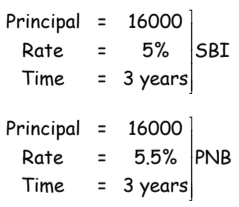

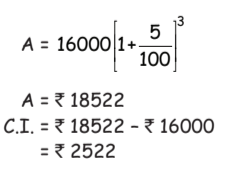 Simple Interest
Simple Interest  = Rs. 2640 Diff.
= Rs. 2640 Diff.
= Rs. 118. [PNB offers a better return]
Q50: By what least number 25920 be divided to obtain a number which is a perfect cube?
(a) 35
(b) 25
(c) 15
(d) 5
 View Answer
View Answer 
Ans: (c) 25920 = 3 × 3 × 3 × 3 × 2 × 2 × 2 × 2 × 2 × 2 × 5
25920 = 3 × 3 × 3 × 3 × 2 × 2 × 2 × 2 × 2 × 2 × 5
The factors 3 and 5 are singled out 3 × 5 = 15 25920 should be divided by 15 to obtain a perfect cube.
|
28 videos|89 docs|91 tests
|
FAQs on Mathematics Olympiad Previous Year Papers - 1 - Mathematics Olympiad Class 7
| 1. What topics are covered in the Class 7 Mathematics Olympiad exam? |  |
| 2. How can I prepare effectively for the Class 7 Mathematics Olympiad? |  |
| 3. Are there any recommended books for Class 7 Mathematics Olympiad preparation? |  |
| 4. What is the format of the Mathematics Olympiad exam for Class 7? |  |
| 5. How is the scoring system structured in the Class 7 Mathematics Olympiad? |  |
















