Mathematics Olympiad Previous Year Papers - 2 | Mathematics Olympiad Class 7 PDF Download
| Table of contents |

|
| Logical Reasoning |

|
| Mathematical Reasoning |

|
| Everyday Mathematics |

|
| Achievers Section |

|
Note: The questions provided in this document are similar to the questions that were asked in the actual Olympiad exam. So, we recommend you study these for your Olympiad preparation
Logical Reasoning
Q1: 42 (4 + 2) = (42 × 4) + (42 × 2) is an example of
(a) closure property
(b) commutative property
(c) associative property
(d) distributive property
 View Answer
View Answer 
Ans: (d)
a (b + c) = (a × b) + (a × c) distributive property.
Q2: Find 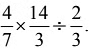
(a) 4
(b) 5
(c) 3
(d) 2
 View Answer
View Answer 
Ans: (a)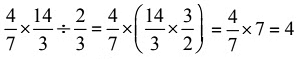
Q3: The property represented by a × (b + c) = a × b + a × c is
(a) commutative property
(b) associative property
(c) distributive property
(d) none of these
 View Answer
View Answer 
Ans: (c)
distributive property
Q4: The number which is neither positive nor negative is
(a) 1
(b) 5
(c) 0
(d) 10
 View Answer
View Answer 
Ans: (c)
0 is neither positive nor negative.
Q5: Madhavi eats one full bar of chocolate. Then she divides another one into 5 equal parts and eats 3 of those parts. The total number of chocolates that she has eaten is
(a) 4/5
(b) 3/5
(c) 8/5
(d) 8/10
 View Answer
View Answer 
Ans: (c)
Q6: If 2805 ¸ 2.55 = 1100, then 280.5 ¸ 25.5 = _______
(a) 1.1
(b) 1.01
(c) 0.11
(d) 11
 View Answer
View Answer 
Ans: (d)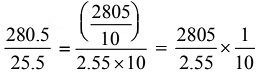
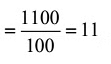
Q7: The rational number 0/7
(a) has a positive numerator.
(b) has a negative numerator.
(c) has either a positive numerator or a negative numerator.
(d) has neither a positive numerator nor a negative numerator.
 View Answer
View Answer 
Ans: (d)
0/7 equals to 0 and 0 is neither positive nor negative.
Q8: π is
(a) rational
(b) irrational
(c) imaginary
(d) an integer
 View Answer
View Answer 
Ans: (b)
π is irrational.
Q9: The largest rational number among the following rational numbers is
(a) 44/34
(b) 55/85
(c) 76/68
(d) 98 /102
 View Answer
View Answer 
Ans: (a)
On equating the denominators, we find that numerator of option (a) is largest and is equal to 132/102.
Q10: How many of the following four numbers are rational?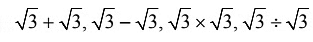 (a) One
(a) One
(b) Two
(c) Three
(d) Four
 View Answer
View Answer 
Ans: (c) Three
Q11: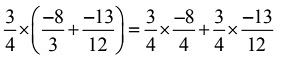
is illustrated by which of the following property?
(a) Commutativity
(b) Associativity of multiplication
(c) Distributivity of multiplication over addition
(d) Existence of identity
 View Answer
View Answer 
Ans: (c)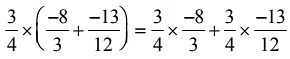 Distributivity of multiplication over addition.
Distributivity of multiplication over addition.
Q12: The reciprocal of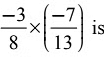
(a)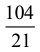 (b)
(b)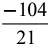 (c)
(c)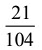 (d)
(d)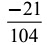
 View Answer
View Answer 
Ans: (a)
Given, 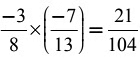 ∴ Reciprocal of
∴ Reciprocal of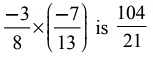
Q13: The sum of two numbers is 80. If three times of one number is equal to five times of the other number, find the numbers.
(a) 20, 60
(b) 50, 30
(c) 10, 70
(d) 25, 55
 View Answer
View Answer 
Ans: (b)
Let numbers are
x and y x + y = 80 ...(i)
Now, 3x = 5y 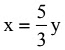
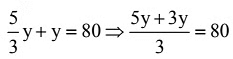
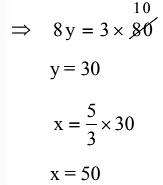
Q14: In an examination a student was asked to find 3 14 th of a certain number. By mistake, he found 3 4 of it. His answer was 150 more than the correct answer. The number is
(a) 290
(b) 280
(c) 240
(d) 180
 View Answer
View Answer 
Ans: (b) Let the required number be x.
We have, 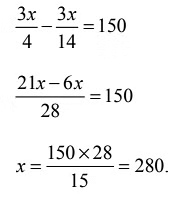
Q15: A man is 5 years older than his wife and the wife is now thrice as old as their daughter, who is 10 years old. How old was the man when his daughter was born?
(a) 20 years
(b) 23 years
(c) 25 years
(d) 30 years
 View Answer
View Answer 
Ans: (c)
Let the age of daughter be x yrs.
Age of wife = 3x
Age of the man = 3x + 5
Given that x = 10
⇒ Age of man = 3 (10) + 5 = 35 years.
∴ Age of the man when his daughter was
born = 35 – 10 = 25 years.
Mathematical Reasoning
Q16: There were only two candidates in an election. One got 62% votes and was elected by a margin of 144 votes. The total number of voters were
(a) 500
(b) 600
(c) 700
(d) 800
 View Answer
View Answer 
Ans: (b)
Let the total number of votes be x.
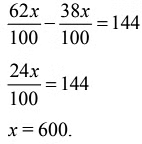
Q17: A man can row at 8 kmph in still water. If the river is running at 2 kmph, it takes him 48 minutes to row to a place and back. How far is the place?
(a) 1 km
(b) 2 km
(c) 3 km
(d) 4 km
 View Answer
View Answer 
Ans: (c) Speed of the man in still water = 8 kmph
Speed of the river = 2 kmph
Downstream = 8 + 2 = 10 kmph
Upstream = 8 – 2 = 6 kmph 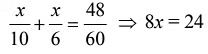 x = 3 km.
x = 3 km.
Q18: If the angles of a triangle are in the ratio 2: 3: 4, then the difference between the greatest and smallest angles is
(a) 10°
(b) 20°
(c) 30°
(d) 40°
 View Answer
View Answer 
Ans: (d)
2x + 3x + 4x = 180°
9x = 180°
x = 20°
Difference = 4x – 2x = 2x = 2 × 20° = 40°.
Q19: One number is three times another. If the larger number is subtracted from 60, the result is 5 less than the smaller number subtracted from 55. Find the numbers.
(a) 5 and 10
(b) 5 and 6
(c) 5 and 15
(d) 15 and 18
 View Answer
View Answer 
Ans: (c)
Let the smaller number = x
Larger number subtracted from 60 = 60 – 3x
Smaller number subtracted from 55 = 55 – x
Solution is x = 5 (smaller no.)
Q20: The hundreds digit of a three-digit number is 7 more than the units digit. The digits of the number are reversed, and the resulting number is subtracted from the original three digit number. The units digit of the final number so obtained is
(a) 0
(b) 1
(c) 2
(d) 3
 View Answer
View Answer 
Ans: (d)
Let unit digit be x
Then, hundreds digit = x + 7
Number = 100(x + 7) + x
= 101x + 700
Now after reverse the new number will be
= 100x + x + 7
= 101x + 7
According to question
Original no. – New no.
= (101 x + 700) – (101x + 7) = 693
So, unit of final no. = 3.
Q21: A bag contains 50P, 25P and 10P coins in the ratio 2:3:4: amounting to Rs. 129. Find the number of coins of each type
(a) 120,180,240
(b) 180,150,200
(c) 200,180,120
(d) 180,200,140
 View Answer
View Answer 
Ans: (a)
Let number of coins of 50P, 25P and 10P are 2x, 3x and 4x respectively
∴ 2x(.50) + 3x (.25) + 4x (.10) = 129
x + .75x + .4x = 129
2.15x = 129 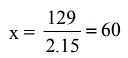 ∴ No. of coins of 50P, 25P and 10P are 120, 180, 240 respectively.
∴ No. of coins of 50P, 25P and 10P are 120, 180, 240 respectively.
Q22: A boat goes downstream and covers the distance between two ports in 4 hrs while it covers the same distance upstream in 5 hrs. If the speed of the stream is 2 kmph, the speed of the boat in still water is
(a) 15 km/ hr
(b) 20 km/ hr
(c) 24 km/ hr
(d) 18 km/ hr
 View Answer
View Answer 
Ans: (d)
Let the speed of the boat in still water be x km/hr.
The speed down stream = (x + 2) km/hr.
The speed up stream = (x – 2) km/hr.
4 (x + 2) = 5 (x – 2) x = 18 km/hr.
Q23: There are 40 passengers in a bus, some with Rs. 3 tickets and remaining with Rs. 10 tickets. The total collection from these passengers is Rs. 295. Find how many passengers have tickets worth Rs. 3?
(a) 23
(b) 19
(c) 15
(d) 11
 View Answer
View Answer 
Ans: (c) Let the passengers have ticket worth Rs. 3 = x Then,
3 × x + 10 × (40 – x) = 295
3x + 400 – 10x = 295
–7x = 295 – 400
–7x = –105 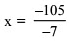 x = 15.
x = 15.
Q24: In a quadrilateral the angles are in the ratio 3 : 4 : 5 : 6. Then the difference between the greatest and the smallest angle is
(a) 108°
(b) 60°
(c) 180°
(d) 360°
 View Answer
View Answer 
Ans: (b) Let the angles be 3x, 4x, 5x, and 6x.
We have
3x + 4x + 5x + 6x = 360°
[sum of angles of a quadrilateral is equal to 360°]
18x = 360°
x = 20°
Difference between greatest and smallest angles = 6x − 3x = 3x = 3 × 20° = 60°.
Q25: The angles of a quadrilateral are x°, x − 10°, x + 30° and 2x°. Find the greatest angle.
(a) 136°
(b) 180°
(c) 68°
(d) None of these
 View Answer
View Answer 
Ans: (a) We have,
x + x − 10 + x + 30 + 2x = 360°
5x + 20 = 360 The angles are 68°, 68° − 10°, 68° + 30°, 2 × 68°,i.e. 68°, 58°, 98°, 136°.∴ Greatest angle = 136°.
The angles are 68°, 68° − 10°, 68° + 30°, 2 × 68°,i.e. 68°, 58°, 98°, 136°.∴ Greatest angle = 136°.
Q26: Find x in the following figure:
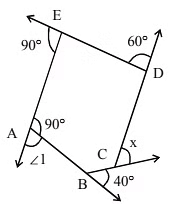
(a) 90°
(b) 70°
(c) 80°
(d) 60°
 View Answer
View Answer 
Ans: (c)
In the given figure
∠1 + 90° = 180°
⇒ ∠1 = 90° (linear pair)
Now, sum of exterior angles of a polygon is 360°, therefore,
x + 60° + 90° + 90° + 40° = 360°
x + 280° = 360°
x = 80°
Q27: In a parallelogram ABCD, diagonals AC and BD intersect at O. If AO = 5 cm, then AC =
(a) 5 cm
(b) 20 cm
(c) 10 cm
(d) None of these
 View Answer
View Answer 
Ans: (c)
Diagonals bisect each other.
We have AC = 2 × AO = 2 × 5 = 10 cm.
Q28. In a rhombus ABCD, if AB = AC, then ∠BCD =
(a) 60°
(b) 120°
(c) 72°
(d) 108°
 View Answer
View Answer 
Ans: (b)
∵ AB = AC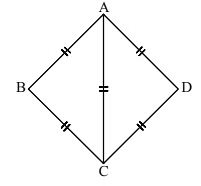 △ABC is an equilateral triangle.So ∠BCA = 60°, also ∠ACD = 60°.∴ ∠BCD = 60° + 60° = 120°.
△ABC is an equilateral triangle.So ∠BCA = 60°, also ∠ACD = 60°.∴ ∠BCD = 60° + 60° = 120°.
Q29: Find the value of x in the figure given below. (2014)
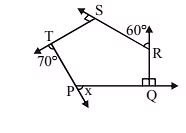
(a) 35°
(b) 50°
(c) 55°
(d) 60°
 View Answer
View Answer 
Ans: (b)
In this pentagon
Sum of external angles = 360°
∠T + ∠S + ∠R + ∠Q + ∠P = 360°
70° + 90° + 60° + 90° + ∠P = 360°
∠P = 50°
Q30: If ABCD is a parallelogram, then ∠A – ∠C = ...........
(a) 180°
(b) 0°
(c) 360°
(d) 90°
 View Answer
View Answer 
Ans: (b)
In a parallelogram, opposite angles are equal.
So ∠A = ∠C ⇒ ∠A − ∠C = 0°.
Q31: The perimeter of a parallelogram is 180 cm. One side exceeds another by 10 cm. The adjacent sides of the parallelogram are........
(a) 30 cm, 40 cm
(b) 40 cm, 50 cm
(c) 50 cm, 60 cm
(d) None of these
 View Answer
View Answer 
Ans: (b) Two sides are x, x + 10
Perimeter = 180 cm
i.e., x + x + 10 + x + x + 10 = 180
4x + 20 = 180
x = 40 cm.
The sides are 40 cm, 50 cm.
Q32: ABCD is a parallelogram in which ∠DAB = 75° and ∠DBC = 60° then ∠CDB = ...........
(a) 60°
(b) 75°
(c) 45°
(d) 135°
 View Answer
View Answer 
Ans: (c)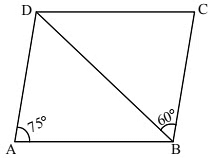 We have,∠ADB = ∠CBD = 60° (∵ AD ∥ BC)In △ADB∠A + ∠D + ∠B = 180°
We have,∠ADB = ∠CBD = 60° (∵ AD ∥ BC)In △ADB∠A + ∠D + ∠B = 180°
75° + 60° + ∠B = 180°
∠B = 45°
∴ ∠ABD = 45°
∴ ∠CDB = ∠ABD = 45°
(Alternate interior angles)
Q33: In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 120°. Find ∠BCD.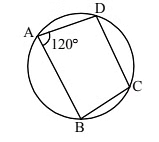 (a) 240°
(a) 240°
(b) 60°
(c) 120°
(d) 180°
 View Answer
View Answer 
Ans: (b)
Sum of the opposite angles in a cyclic quadrilateral = 180°.
∴ ∠BAD + ∠BCD = 180°
∠BCD = 180° − ∠BAD
= 180° − 120° = 60°.
Q34: If ‘*’ represents ‘×’, ‘#’ represents ‘+’, ‘%’ represents ‘–’ and ‘$’ represents ‘÷’, which of the following equations is not correct?
(a) 5 # 6 $ 3 * 4 % 9 = 4
(b) 5 * 9 $ 3 # 4 % 6 = 13
(c) 5 # 3 * 6 $ 2 % 8 = 6
(d) 5 * 6 $ 3 # 4 % 8 = 6
 View Answer
View Answer 
Ans: (c)
- To solve the equations, we need to replace the symbols:
- ‘*’ with ‘×’, ‘#’ with ‘+’, ‘%’ with ‘–’, and ‘$’ with ‘÷’.
- For option (c): 5 + 3 × 6 ÷ 2 – 8 becomes 5 + 18 ÷ 2 – 8 = 5 + 9 – 8 = 6, which is correct.
- However, the calculations for the other options show that they do not equal the stated results, making option (c) the only incorrect equation.
Q35: Arrange the following words in the order they appear in the dictionary and choose the right option.
(a) Folder
(b) Finger
(c) Fountain
(d) Figure
(e) Flight
 View Answer
View Answer 
Ans: (d)
- To determine the correct order, we look at the first letters of each word: F for Folder, Finger, Fountain, Figure, and Flight.
- Next, we compare the second letters: Folder (o), Finger (i), Fountain (o), Figure (i), and Flight (l).
- Following this, we can see that Finger comes before Figure because 'i' is the same, but 'g' comes after 'n'.
- Finally, the correct sequence is Finger, Figure, Flight, Folder, Fountain, which corresponds to option (d).
Everyday Mathematics
Q36: Pointing to a girl at a gathering, Gopal remarked, “She is the daughter of my son’s wife.” What is Gopal's relationship to that girl?(a) Grandmother
(b) Aunt
(c) Granddaughter
(d) Daughter-in-law
 View Answer
View Answer 
Ans: (c)
- The girl is described as the daughter of Gopal's son's wife. This means she is the child of Gopal's son.
- Since Gopal is the grandfather of this girl, she is his granddaughter.
- Thus, the correct relationship is that the girl is Gopal's granddaughter.
- Options like grandmother and aunt do not fit the relationship described.
Q37: If ‘METAL’ is coded as ‘72856’ and ‘MIND’ is coded as ‘7341’, then how will ‘DILEMMA’ be coded in that code language?
(a) 7362115
(b) 1362775
(c) 1328776
(d) 7352775
 View Answer
View Answer 
Ans: (b)
- To decode the word 'DILEMMA', we first need to understand the coding system used for the letters.
- From the examples, we see that each letter corresponds to a specific number: M=7, E=2, T=8, A=5, L=6, I=3, N=4, and D=1.
- Using this code, we can break down 'DILEMMA' as follows: D=1, I=3, L=6, E=2, M=7, M=7, A=5.
- Putting these numbers together gives us the code: 1362775.
Q38: How many of the following expressions qualify as binomials? 5a² + 3b, 2a + 3b, 8a², 9a² + 5a + 3b², 7ab + 3a²
(a) 3
(b) 2
(c) 4
(d) 5
 View Answer
View Answer 
Ans: (a)
- To determine how many expressions are binomials, we need to understand that a binomial is a polynomial with exactly two terms.
- Looking at the expressions: 5a² + 3b (2 terms), 2a + 3b (2 terms), 8a² (1 term), 9a² + 5a + 3b² (3 terms), and 7ab + 3a² (2 terms).
- Only the expressions 5a² + 3b, 2a + 3b, and 7ab + 3a² are binomials, totaling 3 binomials.
- Thus, the correct answer is (a) 3.
Q39: Which of the following statements is CORRECT?
(a) All natural numbers are whole numbers and all whole numbers are integers.
(b) All whole numbers are integers and all integers are natural numbers.
(c) All integers are whole numbers and all natural numbers are integers.
(d) All integers are whole numbers and all integers are natural numbers.
 View Answer
View Answer 
Ans: (a)
- The statement in option (a) is correct because natural numbers (like 1, 2, 3...) are indeed a subset of whole numbers (which include 0 and all natural numbers).
- Furthermore, whole numbers are a subset of integers (which include negative numbers, zero, and positive numbers).
- Options (b), (c), and (d) are incorrect because they misrepresent the relationships between these sets of numbers.
- Understanding these relationships helps clarify how different types of numbers are categorized in mathematics.
Q40: How many unique prime factors does the smallest 5-digit number possess?
(a) 2
(b) 3
(c) 4
(d) 5
 View Answer
View Answer 
Ans: (a)
- The smallest 5-digit number is 10,000.
- To find its prime factors, we can break it down: 10,000 = 10 x 10 x 10 x 10 = (2 x 5) x (2 x 5) x (2 x 5) x (2 x 5).
- This simplifies to 2^4 x 5^4, showing that the only distinct prime factors are 2 and 5.
- Thus, the total number of distinct prime factors is 2.
Q41: Two numbers are in the ratio of 2:3. If 2 is taken away from the smaller number and 6 is taken away from the larger number, the ratio changes to 3:4. What is the total of the two numbers?
(a) 50
(b) 38
(c) 45
(d) 25
 View Answer
View Answer 
Ans: (a)
- Let the two numbers be 2x and 3x based on the ratio 2:3.
- After subtracting, the smaller number becomes 2x - 2 and the larger number becomes 3x - 6.
- The new ratio is given as (2x - 2) / (3x - 6) = 3 / 4.
- Cross-multiplying gives 4(2x - 2) = 3(3x - 6), leading to 8x - 8 = 9x - 18.
- Solving this gives x = 10. Therefore, the numbers are 20 and 30.
- The sum of the two numbers is 20 + 30 = 50.
Q42: What is the smallest number that, when reduced by 4, can be evenly divided by 10, 15, 20, and 25?
(a) 304
(b) 296
(c) 354
(d) 350
 View Answer
View Answer 
Ans: (a)
- To find the least number, we first need to determine the least common multiple (LCM) of the numbers 10, 15, 20, and 25.
- The LCM of these numbers is 300.
- Now, we need to add 4 to this LCM to find the smallest number that meets the condition: 300 + 4 = 304.
- Thus, 304 is the least number that, when decreased by 4, is divisible by 10, 15, 20, and 25.
Q43: What needs to be deducted from the largest 6-digit number created using the digits 5, 3, 6, 8, and 4 (with each digit used at least once) to equal 100000?
(a) 766543
(b) 582614
(c) 786543
(d) None of these
 View Answer
View Answer 
Ans: (c)
- To find the largest 6-digit number, we arrange the digits 8, 7, 6, 5, 4, and 3 in descending order, which gives us 876543.
- Next, we need to determine what to subtract from this number to reach 100000.
- Calculating this gives us: 876543 - 100000 = 776543.
- Among the options, the correct answer is 786543, which is the number we need to subtract to achieve the target.
Q44: In a game, team P recorded scores of –40, 10, 50, –20, and 15 points, while team Q had scores of 40, –20, –10, 30, and 20 points over five consecutive rounds. Which team had a higher total score and by what margin?
(a) P, 30 points
(b) Q, 40 points
(c) Q, 45 points
(d) P, 25 points
 View Answer
View Answer 
Ans: (c)
- To find out which team scored more, we need to calculate the total points for each team.
- For team P: –40 + 10 + 50 + –20 + 15 = 15 points.
- For team Q: 40 + –20 + –10 + 30 + 20 = 60 points.
- Team Q scored 45 points more than team P (60 - 15 = 45).
Q45: A rectangular piece of land is to be sold off in smaller pieces. The total area of the land is 217 sq. miles. Each piece to be cut out is 162 sq. miles in size. How many smaller pieces of the land can be sold at the given size?
(a) 215
(b) 164
(c) 29
(d) None of these
 View Answer
View Answer 
Ans: (c)
- To find out how many smaller pieces can be sold, we need to divide the total area of the land by the area of each piece.
- The total area is 217 sq. miles and each piece is 162 sq. miles.
- So, we calculate: 217 ÷ 162, which gives us approximately 1.34.
- This means only 1 full piece can be sold, as we cannot sell a fraction of a piece. Therefore, the answer is 29 pieces can be sold at the given size.
Achievers Section
Q46: Megha is 20 years younger than her mother. After 10 years, her mother will be twice as old as Megha. Find the present age of Megha.(a) 15 years
(b) 12 years
(c) 10 years
(d) 18 years
 View Answer
View Answer 
Ans: (c)
- Let Megha's current age be x. Then her mother's age is x + 20.
- In 10 years, Megha will be x + 10 and her mother will be (x + 20) + 10 = x + 30.
- According to the problem, in 10 years, her mother will be twice Megha's age: x + 30 = 2(x + 10).
- Simplifying this gives: x + 30 = 2x + 20, leading to 30 - 20 = 2x - x, so x = 10.
- Thus, Megha's present age is 10 years.
Q47: Out of 6 varieties of ice creams, Sneha is interested in buying the chocolate flavor that is favored the most by children. Which measure of central tendency would be the best choice if she receives the data?
(a) Mean
(b) Median
(c) Mode
(d) Range
 View Answer
View Answer 
Ans: (c)
- The mode is the measure of central tendency that identifies the most frequently occurring value in a dataset.
- In this case, since Sneha wants to know which chocolate ice cream is the most liked by children, the mode will show her the flavor that appears the most in the data.
- The mean and median are not suitable here because they provide average values or middle values, which do not directly indicate popularity.
- The range simply shows the difference between the highest and lowest values, which is not helpful for determining preference.
Q48: Read the given statements carefully and state T for true and F for false.
(i) The value of ((-71 - (-45)) times (70 - 50) + 400) is -120.
(ii) ( -78) should be subtracted from the product of 15 and (-8) to get -198.
(iii) The value of (a + (b + c) - (a + b) + c) for (a = 5), (b = -2), and (c = 3), is 0.
(a) F T F
(b) T F F
(c) T F T
(d) F F T
 View Answer
View Answer 
Ans: b
- Statement (i): The calculation gives a value of 120, not -120, so this is false.
- Statement (ii): The product of 15 and -8 is -120. Subtracting -78 from -120 gives -198, making this statement true.
- Statement (iii): Plugging in the values results in 0, confirming this statement is true.
- Thus, the correct combination of true and false is T F F, which corresponds to option b.
Q49: Read the given statements carefully and select the correct option.
Statement-I: If the median of the observations 15, 17, 20, 20, 24, a + 5, 29, 31, 31, 33, 34 (arranged in ascending order) is 27, then the mean of the above data is 20.
Statement-II: The median and mode of the given data, 70, 52, 47, 64, 47, 71, 58 are 58 and 47 respectively.
(a) Both Statement-I and Statement-II are true.
(b) Statement-I is true but Statement-II is false.
(c) Both Statement-I and Statement-II are false.
(d) Statement-I is false but Statement-II is true.
 View Answer
View Answer 
Ans: (d)
- Statement-I: The median is the middle value when data is arranged in order. Here, if the median is 27, it implies that the value of a + 5 must be adjusted accordingly. However, the mean being 20 is incorrect based on the given median.
- Statement-II: The median of the data set 70, 52, 47, 64, 47, 71, 58 is indeed 58, and the mode, which is the most frequently occurring number, is 47. This statement is true.
- Since Statement-I is incorrect and Statement-II is correct, the answer is (d).
Q50: Solve the following:
(i) An item sold through two dealers has a profit of 38% based on the original cost price. If the first dealer earns a profit of 20%, what is the profit percentage for the second dealer?
(ii) In an office with 125 employees, 15 are not present, and 10% of those remaining did not meet their target. Calculate the number of employees who met their target.
(a) 15%, 90
(b) 10%, 88
(c) 15%, 99
(d) None of these
 View Answer
View Answer 
Ans: (c)
- To find the profit percentage of the second dealer, we first calculate the selling price after the first dealer's profit of 20%.
- The second dealer then sells the item at a total profit of 38%, which means we can find the second dealer's profit by comparing the selling price to the cost price.
- For the office scenario, after accounting for the 15 absentees, there are 110 employees left. If 10% of these did not achieve their target, that means 10 employees failed, leaving 100 who did achieve their target.
- Thus, the answer is 15% for the first part and 99 for the second part, leading to option (c) as the correct choice.
|
28 videos|89 docs|91 tests
|
FAQs on Mathematics Olympiad Previous Year Papers - 2 - Mathematics Olympiad Class 7
| 1. What topics are covered in the Class 7 Mathematics Olympiad previous year papers? |  |
| 2. How can I prepare effectively for the Class 7 Mathematics Olympiad? |  |
| 3. What is the format of the Class 7 Mathematics Olympiad exam? |  |
| 4. Are there any specific strategies for solving Logical Reasoning questions in the Olympiad? |  |
| 5. How can previous year papers help in Olympiad preparation? |  |















