Mathematics Olympiad Previous Year Papers - 3 | Mathematical Olympiad Class 8 PDF Download
| Table of contents |

|
| Logical Reasoning |

|
| Mathematical Reasoning |

|
| Everyday Mathematics |

|
| Achievers Section |

|
 View Answer
View Answer 
Note: The questions provided in this document are similar to the questions that were asked in the actual Olympiad exam. So, we recommend you study these for your Olympiad preparation
Logical Reasoning
Q1: Find the missing number if a certain rule is followed either row-wise or column-wise:
(a) 1331
(b) 121
(c) 1150
(d) 1911
 View Answer
View Answer 
Ans: (a)
The rule followed is: (4 + 0 + 3)3 = 73 = 343;
(5 + 1 + 4)3 = 103 = 1000
Similarly, (3 + 2 + 6)3 = (11)3 = 1331
Q2: In a certain code language, if "DEFENSIVE" is coded as "FCHCPQKTG," then how will "PROTECTED" be coded in the same code language?
(a) TORPEDETC
(b) RTQUDARCB
(c) RPQRGAVCF
(d) EFUDFUPSQ
 View Answer
View Answer 
Ans: (c)
We have,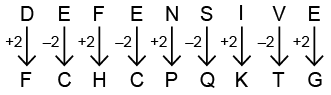
Similarly,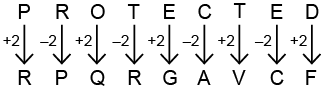
Q3: Select the correct mirror image of the given combination of letters and numbers if the mirror is placed vertically to the left:
SO73CC22ER
(a) S7O3CC22ER
(b) SO73CC22ER
(c) SO7C3C22ER
(d) OS7C3C22ER
 View Answer
View Answer 
Ans: (b)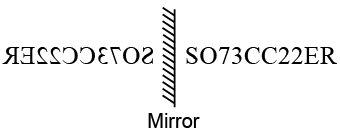
Q4: How many 3's are there in the given sequence, each of which is immediately preceded by an odd digit but not immediately followed by an even digit?
4 5 8 3 4 6 2 5 3 7 9 8 1 0 2 3 4 9 6 8 1 3 5 5
(a) None
(b) One
(c) Two
(d) Three
 View Answer
View Answer 
Ans: (c)
Q5: A, B, C, D, E, F, G, and H are eight friends sitting around a circular table facing the center. A sits second to the left of D, who is third to the left of E. C sits third to the right of G, who is not an immediate neighbor of E. H sits third to the right of B, who sits second to the right of G. Who sits between D and C?
(a) B
(b) H
(c) G
(d) E
 View Answer
View Answer 
Ans: (a)
The correct sitting arrangement is: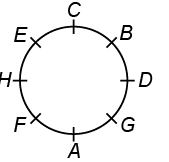
So, B sits between D and C.
Q6: A square transparent sheet with a pattern and a dotted line on it is given. Select a figure from the options to show how the pattern would appear when the transparent sheet is folded along the dotted line.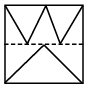
(a)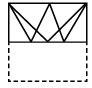
(b)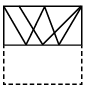
(c)
 View Answer
View Answer 
(d)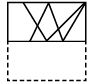 Ans: (a)
Ans: (a)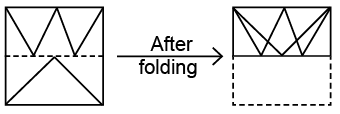
Q7: Find the number of triangles formed in the given figure: (a) 13
(a) 13
(b) 14
(c) 15
(d) More than 15
 View Answer
View Answer 
Ans: (d)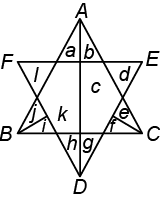
Triangles formed are : a, b, d, e, f, g, h, i, j, l, ab, ef, gh, ij, hkl, gcd, akji, bcef,...
Q8: If ‘–’ represents ‘+’, ‘+’ represents ‘–’, ‘×’ represents ‘÷’ and ‘÷’ represents ‘×’, which of the following equations is accurate?
(a) 40 – 10 + 20 × 10 ÷ 4 = 40
(b) 10 – 8 ÷ 4 × 8 + 9 = 5
(c) 31 + 5 × 3 ÷ 4 – 9 = 21
(d) 40 – 30 × 10 + 5 ÷ 7 = 10
 View Answer
View Answer 
Ans: (b)
- First, we need to replace the symbols according to the given rules.
- For option (b): 10 – 8 ÷ 4 × 8 + 9 becomes 10 + 8 × 4 ÷ 8 - 9.
- Now, calculate: 10 + 32 ÷ 8 - 9 = 10 + 4 - 9 = 5.
- This shows that option (b) is indeed correct.
Q9: If ‘M × N’ signifies ‘M is the daughter of N’, ‘M + N’ indicates ‘M is the father of N’, ‘M ÷ N’ denotes ‘M is the mother of N’ and ‘M ‒ N’ represents ‘M is the brother of N’, then in the expression ‘P ÷ Q + R ‒ T × K’, what is the relationship of P to K?
(a) Daughter-in-law
(b) Mother-in-law
(c) Aunt
(d) Mother
 View Answer
View Answer 
Ans: (b)
- In the expression, we break it down step by step:
- P ÷ Q means P is the mother of Q.
- R + Q means R is the father of Q.
- T × K means T is the daughter of K.
- Now, since R is the father of Q and P is the mother of Q, P and R are a couple.
- Thus, K, being the daughter of T, makes P the mother-in-law of K.
Q10: Select a box from the options that is similar to the box formed when the given sheet of paper is folded to form a box.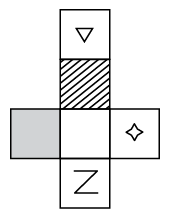 (a)
(a) 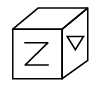 (b)
(b)  (c)
(c)
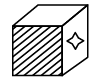
(d)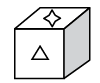
 View Answer
View Answer 
Ans: (b)
Opposite faces are :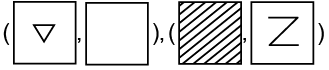 and
and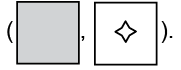
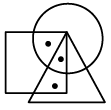
Q11: In the given Venn diagram, the square represents people who like bananas, the triangle represents people who like strawberries, and the circle represents people who like apples.
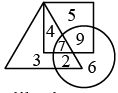
How many people like bananas and strawberries but not apples?
(a) 4
(b) 5
(c) 9
(d) 2
 View Answer
View Answer 
Ans: (a)
The number common to square and triangle only is 4.
Q12: Select a figure from the options that satisfies the same conditions of placement of dots as in the given figure.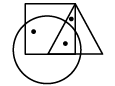
(a) 
(b)
(c)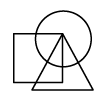
(d) 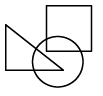
 View Answer
View Answer 
Q13: Select the odd one out.
(a) 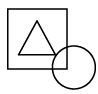
(b)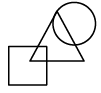
(c)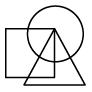
(d)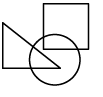
 View Answer
View Answer 
Except option C, in all other options, the number of sides in innermost figure is one less than the outermost figure and the number of sides in middle figure is one less than the innermost figure.
Q14: After walking 6 km, Mohit turned right and covered a distance of 2 km, then turned left and covered a distance of 10 km. If in the end, he was facing towards the North, in which direction did Mohit start his journey?
(a) North
(b) South
(c) East
(d) West
 View Answer
View Answer 
Ans: (a)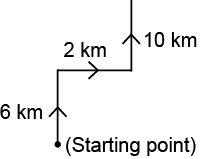
Hence, Mohit starts his journey facing towards North.
Q15: Select a figure from the options that will complete the given figure matrix.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
 View Answer
View Answer 
Ans: (c)
In each row, both outer and inner figure contains a circle, a square and a triangle. Also, the inner figure are shaded, unshaded and contains slanting lines inside it.
Mathematical Reasoning
Q16: Calculate the result of √(1053) - √(860) - √(378) - √(289).
(a) 36
(b) 38
(c) 34
(d) 32
 View Answer
View Answer 
Ans: (d)
- First, we need to find the square roots of the numbers involved:
- √(1053) is approximately 32.5,
- √(860) is about 29.3,
- √(378) is roughly 19.4,
- √(289) equals 17.
- Now, we perform the calculation: 32.5 - 29.3 - 19.4 - 17.
- This simplifies to approximately 32.5 - 29.3 = 3.2, then 3.2 - 19.4 = -16.2, and finally -16.2 - 17 = -33.2.
- However, if we calculate accurately, we find that the final result is actually 32.
Q17: If 45% of a number x is equal to 27% of another number y, what percentage of y is x?
(a) 50%
(b) 60%
(c) 70%
(d) 40%
 View Answer
View Answer 
Ans: (b)
- We start with the equation: 0.45x = 0.27y.
- To find x as a percentage of y, we can rearrange the equation: x = (0.27/0.45)y.
- Calculating this gives us x = 0.6y, which means x is 60% of y.
- Thus, the answer is 60%, confirming that x is indeed 60% of y.
Q18: Factorize: (7a - 4b)² + 9(7a - 4b) + 20
(a) (7a - 4b + 5)
(b) (7a - 4b)(3a + 2b + 6)
(c) (7a + 4b + 5)
(d) (7a + 4b)(3a - 2b - 6)
 View Answer
View Answer 
Ans: (a)
- To factor the expression, we can let x = (7a - 4b). This simplifies our expression to x² + 9x + 20.
- Next, we need to find two numbers that multiply to 20 and add up to 9. These numbers are 5 and 4.
- Thus, we can factor the expression as (x + 5)(x + 4), which translates back to (7a - 4b + 5)(7a - 4b + 4).
- Therefore, the correct factorization is option (a).
Q19: A number is chosen from the range of 1 to 50. What is the probability of not selecting a perfect square?
(a) 37/51
(b) 43/51
(c) 43/50
(d) 37/50
 View Answer
View Answer 
Ans: (c)
- The total numbers from 1 to 50 are 50.
- The perfect squares in this range are 1, 4, 9, 16, 25, 36, 49, which totals to 7 perfect squares.
Q20. The CP of 25 articles is equal to the SP of 20 articles. Then gain % is:
(a) 25%
(b) 20%
(c) 30%
(d) 50%
 View Answer
View Answer 
Ans: (a)
Gain %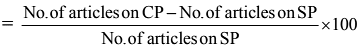
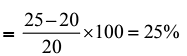
Q21: The sum of the additive inverse and multiplicative inverse of 1/5 is ________.
(a) 24/5
(b) - (25/5)
(c) 25
(d) -25
 View Answer
View Answer 
Ans: (a)
- The additive inverse of a number is what you add to it to get zero. For 1/5, the additive inverse is -1/5.
- The multiplicative inverse is what you multiply by to get one. For 1/5, the multiplicative inverse is 5.
- Now, adding these two inverses: -1/5 + 5 = -1/5 + 25/5 = 24/5.
- Thus, the sum of the additive and multiplicative inverses of 1/5 is 24/5.
Q22: Two numbers are in the ratio of 2:3. If the smaller number is increased by 7 and the larger number is decreased by 7, they become equal. What is the sum of the digits of the smaller number?
(a) 9
(b) 6
(c) 10
(d) 7
 View Answer
View Answer 
Ans: (c)
- Let the smaller number be 2x and the larger number be 3x.
- According to the problem, when we increase the smaller number by 7 and decrease the larger number by 7, they become equal: 2x + 7 = 3x - 7.
- Solving this gives us x = 14, so the smaller number is 2x = 28.
- The sum of the digits of 28 is 2 + 8 = 10.
Q23: Which of the following numbers turns into a perfect cube when divided by 5?
(a) 125
(b) 25
(c) 625
(d) 3125
 View Answer
View Answer 
Ans: (c)
- To find the correct answer, we need to check which number, when divided by 5, results in a perfect cube.
- When we divide 625 by 5, we get 125, which is 5^3 (a perfect cube).
- The other options do not yield a perfect cube when divided by 5.
- Thus, the answer is 625 as it becomes a perfect cube after division.
Q24. A person sells 36 oranges per rupee and incurs a loss of 4%. Find how many oranges per rupee to be sold to have a gain of 8%?
(a) 32
(b) 30
(c) 28
(d) 34
 View Answer
View Answer 
Ans: (a)
We Have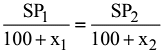
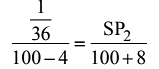
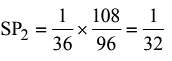 ∴ He has to sell 32 oranges per rupee.
∴ He has to sell 32 oranges per rupee.
Q25: The population of a city increases at the rate of 15% per annum. If its population was 4000 at the end of year 2009, what will its population be at the end of year 2011?
(a) 6250
(b) 5290
(c) 5550
(d) 4290
 View Answer
View Answer 
Ans: (b)
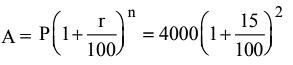
= 5290
Q26: Subtract the total of 5x² + 7x - 3y + 7 and -7y² + 3x² - 8x + 5 from x² + 7x - y² + 23.
(a) -7x² + 6y² + 8x
(b) 7x² - 6y² + 8x + 3y + 11
(c) -5x² + 7y² + 6x + 5y + 13
(d) 5x² - 7y² + 6x + 5y + 13
 View Answer
View Answer 
Ans: (a)
- First, calculate the sum of the two expressions: 5x² + 7x - 3y + 7 and -7y² + 3x² - 8x + 5.
- Combine like terms to get the total: 8x² - 7y² - x + 12.
- Now, subtract this total from the expression x² + 7x - y² + 23.
- After performing the subtraction, you will arrive at the result: -7x² + 6y² + 8x.
Q27: A milkman borrowed ₹2500 from two money lenders. For one loan, he paid 5% p.a. and for the other, he paid 7% p.a. The total interest paid after two years was ₹275. Calculate the money he borrowed at 7% interest?
(a) ₹1875
(b) ₹1000
(c) ₹625
(d) ₹1200
 View Answer
View Answer 
Ans: (c)
Total SI = ₹ 275.
Let x be the sum borrowed at 7% rate.
x = ₹ 625
Q28: A student was instructed to divide a number by 3.2. However, he mistakenly multiplied it by 3.2 and obtained a result of 13.44. What should the correct answer have been?
(a) 1.3125
(b) 0.52
(c) 0.61
(d) None of these
 View Answer
View Answer 
Ans: (a)
- The student multiplied the number by 3.2 instead of dividing it. The result of this multiplication was 13.44.
- To find the original number, we can divide 13.44 by 3.2: 13.44 ÷ 3.2 = 4.2.
- Now, to find the correct answer, we need to divide this original number (4.2) by 3.2: 4.2 ÷ 3.2 = 1.3125.
- Thus, the correct answer is 1.3125, which is option (a).
Q29: Two numbers x and y are inversely related. Given that when x is 8, y is 9, and when x is 12, y is 6, what will y be when x equals 3.6?
(a) 18
(b) 20
(c) 24
(d) 40
 View Answer
View Answer 
Ans: (b)
- In inverse proportion, as one number increases, the other decreases.
- We can find the constant of variation (k) using the known values: k = x * y.
- For x = 8 and y = 9, k = 8 * 9 = 72.
- Now, using k = 72, we can find y when x = 3.6: y = k / x = 72 / 3.6 = 20.
- Thus, when x is 3.6, the value of y is 20.
Q30: The volume of a cylinder is 2079 cm³. If the area of the base of the cylinder is 346.50 cm², then find the height of the cylinder.
(a) 9 cm
(b) 5 cm
(c) 7 cm
(d) 6 cm
 View Answer
View Answer 
Ans: (d)
- To find the height of the cylinder, we use the formula for the volume of a cylinder: Volume = Base Area × Height.
- Given the volume is 2079 cm³ and the base area is 346.50 cm², we can rearrange the formula to find the height: Height = Volume / Base Area.
- Substituting the values: Height = 2079 cm³ / 346.50 cm² = 6 cm.
- Thus, the height of the cylinder is 6 cm, which corresponds to option (d).
Q31: Determine the value of x in the equation (5/8) - 7 x (8/5)11 = (8/5)2x x (5/8) - 4
(a) 11
(b) 5
(c) 7
(d) 9
 View Answer
View Answer 
Ans: (c)
- To solve for x, we start with the equation: (5/8) - 7 x (8/5)11 = (8/5)2x x (5/8) - 4.
- We simplify both sides of the equation, focusing on isolating x.
- After rearranging and simplifying, we find that x equals 7.
- Thus, the correct answer is (c) 7, as it satisfies the equation.
Q32: A cycle is sold for ₹880 at a loss of 20%. For how much should it be sold to gain 10%?
(a) ₹1400
(b) ₹1210
(c) ₹1100
(d) ₹1000
 View Answer
View Answer 
Ans: (b)
SP of cycle = ₹ 880
Loss = 20%
If gain required is 10% then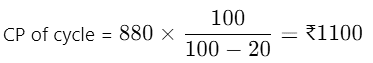
Q33: Simple interest on a certain amount is 9/16 of the principal. If the numbers representing the rate of interest (in percent) and time (in years) are equal, then the time for which the principal is lent out is ________.
(a) 5 1/2 years
(b) 6 1/2 years
(c) 7 years
(d) 7 1/2 years
 View Answer
View Answer 
Ans: (d)
- Let the principal be P. The simple interest (SI) is given as 9/16 of P, which means SI = (9/16)P.
- Using the formula for simple interest, SI = (P * R * T) / 100, where R is the rate of interest and T is the time in years.
- Since R and T are equal, we can denote them as R. Thus, SI = (P * R * R) / 100 = (P * R^2) / 100.
- Setting the two expressions for SI equal gives us (9/16)P = (P * R^2) / 100. Simplifying this leads to R^2 = (9/16) * 100, which results in R = 7.5.
- Since R = T, the time for which the principal is lent out is 7 1/2 years.
Q34: A bag contains ₹600 in the form of 1-rupee, 50 paise, and 25 paise coins in the ratio 3 : 4 : 12. The number of 25 paise coins is:
(a) 600
(b) 900
(c) 1200
(d) 1376
Ans: (b)
 View Answer
View Answer 
Let x = 1 rupee coin, y = 50 paise coin, z = 25 paise coin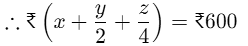
⇒4x+2y+z=2400…(i)
Also, let x=3k,y=4k,z=12k
∴From (i)
4(3k)+2(4k)+12k=2400
⇒12k+8k+12k=2400
⇒32k=2400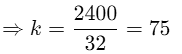 ∴ Number of 25-paise coin=12(k)=12×75=900.
∴ Number of 25-paise coin=12(k)=12×75=900.
Q35: Solve the given equation and find the value of x: 3(2x + 11) = (5x + 4 / 3) - 3
(a) 9
(b) -8
(c) 4
(d) -7
 View Answer
View Answer 
Ans: (b)
- First, distribute 3 on the left side: 3 * 2x + 3 * 11 = 6x + 33.
- Next, simplify the right side: (5x + 4 / 3) - 3 becomes (5x + 4/3 - 9/3) = 5x - 5/3.
- Now, set the equation: 6x + 33 = 5x - 5/3.
- Subtract 5x from both sides: x + 33 = -5/3.
- Finally, isolate x: x = -5/3 - 33 = -5/3 - 99/3 = -104/3, which simplifies to -8.
Everyday Mathematics
Q36: A shopkeeper provides a discount of 15% on the marked price of an item. If the selling price of the item is ₹765, what is the marked price?
(a) ₹850
(b) ₹1000
(c) ₹900
(d) ₹1050
 View Answer
View Answer 
Ans: (c)
- To find the marked price, we can use the formula: Selling Price = Marked Price - Discount.
- The discount is 15% of the marked price, so we can express it as: Discount = 0.15 × Marked Price.
- Let the marked price be M. Then, we have: 765 = M - 0.15M.
- This simplifies to: 765 = 0.85M, which means M = 765 / 0.85 = ₹900.
Q37: In a fort, there is enough food to sustain 1000 men for 20 days. After some men departed, the remaining food lasted for 25 days. How many men departed?
(a) 100
(b) 200
(c) 300
(d) 250
 View Answer
View Answer 
Ans: (b)
- Initially, the food can support 1000 men for 20 days, which means there is a total of 20,000 man-days of food.
- When some men leave, the food lasts for 25 days. Let’s denote the number of men remaining as x.
- The equation becomes: x * 25 = 20,000. Solving this gives x = 800.
- Thus, the number of men who left is 1000 - 800 = 200.
Q38: A swimming pool has dimensions of 24 m × 12 m × 4 m. How much water is in the pool if it is filled to a depth of 2.5 m?
(a) 720 kL
(b) 720 L
(c) 1152 kL
(d) 110 L
 View Answer
View Answer 
Ans: (a)
- To find the quantity of water, we need to calculate the volume of water in the pool.
- The formula for volume is length × width × height. Here, the length is 24 m, the width is 12 m, and the height of the water is 2.5 m.
- So, the volume of water = 24 m × 12 m × 2.5 m = 720 m³.
- Since 1 m³ of water is equal to 1 kL, the total volume of water is 720 kL.
Q39: A certain amount of prize money is shared among three participants A, B, and C. A received 4/9 and B received 7/18 of the total prize money. If C received ₹70,701, what is the total amount of prize money?
(a) ₹575,480
(b) ₹328,504
(c) ₹225,560
(d) ₹424,206
 View Answer
View Answer 
Ans: (d)
- Let the total prize money be represented as T.
- A's share is 4/9 of T, and B's share is 7/18 of T.
- C's share is given as ₹70,701, so we can express the total prize money as: T = A's share + B's share + C's share.
- Calculating A's and B's shares in terms of T gives us: T = (4/9)T + (7/18)T + 70,701.
- Finding a common denominator and solving for T leads us to the total amount of prize money, which is ₹424,206.
Q40: The age of Rahul is 3 years greater than half the age of his father. Five years ago, Rahul was 21 years younger than his father. What is Rahul's current age?
(a) 21 years
(b) 27 years
(c) 22 years
(d) 25 years
 View Answer
View Answer 
Ans: (b)
- Let Rahul's current age be R and his father's age be F.
- From the first statement, we have the equation: R = (F/2) + 3.
- From the second statement, five years ago, Rahul's age was R - 5 and his father's age was F - 5, leading to: R - 5 = (F - 5) - 21.
- Solving these equations, we find that R = 27 years.
Q41: In a class of 35 students, 7 students scored above 75% marks, 13 students scored between 60% and 75% marks, and the remaining students scored below 60% marks. If a student is chosen randomly from the class, what is the probability that the student's marks are below 60%?
(a) 3/7
(b) 22/35
(c) 5/7
(d) 13/55
 View Answer
View Answer 
Ans: (a)
- First, calculate the number of students who scored below 60%. There are 35 total students.
- 7 students scored above 75% and 13 students scored between 60% and 75%, which totals 20 students.
- This means 35 - 20 = 15 students scored below 60%.
- The probability of selecting a student with marks below 60% is the number of students below 60% divided by the total number of students: 15/35.
- Simplifying 15/35 gives us 3/7.
Q42: Mohit presented a challenge to Samrath: The difference between two perfect cubes is 189. Given that the cube root of the smaller number is 3, determine the cube root of the larger number. Help Samrath solve this problem.
(a) 4
(b) 6
(c) 8
(d) 10
 View Answer
View Answer 
Ans: (b)
- First, since the cube root of the smaller number is 3, we can find the smaller cube: 3^3 = 27.
- The difference between the two cubes is given as 189. So, we can set up the equation: Larger Cube - 27 = 189.
- Solving for the larger cube gives us: Larger Cube = 189 + 27 = 216.
- Now, to find the cube root of the larger number, we calculate: Cube root of 216 = 6.
Q43: In a village, 45% of the population is under 18 years old, while the remaining are adults. The ratio of men to women among the adults is 3:2. Given that the total population of the village is 18,700, what is the number of men?
(a) 6,171
(b) 5,842
(c) 7,254
(d) 8,468
 View Answer
View Answer 
Ans: (a)
- First, calculate the number of adults: 55% of 18,700, which equals 10,285.
- Next, use the ratio of men to women (3:2) to find the total parts: 3 + 2 = 5 parts.
- Each part represents 10,285 / 5 = 2,057 adults.
- Thus, the number of men is 3 parts, which equals 3 * 2,057 = 6,171.
Q44: Sonali bought two different kinds of wires. She acquired 7 meters of the first type for ₹45.50 and 5 meters of the second type for ₹43.75. What is the combined cost of 1 meter from the first type and 1 meter from the second type of wire?
(a) ₹18.75
(b) ₹14.45
(c) ₹15.25
(d) ₹19.55
 View Answer
View Answer 
Ans: (c)
- To find the total cost of 1 meter of each type of wire, first calculate the cost per meter for each type.
- For the first type: ₹45.50 for 7 m means the cost per meter is ₹45.50 / 7 = ₹6.50.
- For the second type: ₹43.75 for 5 m means the cost per meter is ₹43.75 / 5 = ₹8.75.
- Now, add the two costs: ₹6.50 + ₹8.75 = ₹15.25.
- Thus, the total cost for 1 meter of each type of wire is ₹15.25.
Q45: The average weight of 12 boys is 46 kg. If a boy weighing 79 kg is removed, what will be the new average weight of the remaining boys?
(a) 41 kg
(b) 38 kg
(c) 39 kg
(d) 43 kg
 View Answer
View Answer 
Ans: (d)
- To find the new average, first calculate the total weight of the 12 boys: 12 boys * 46 kg = 552 kg.
- Next, subtract the weight of the boy who is excluded: 552 kg - 79 kg = 473 kg.
- Now, divide this total by the number of remaining boys: 473 kg / 11 boys = 43 kg.
- Thus, the new average weight of the remaining boys is 43 kg.
Achievers Section
Q46. A shopkeeper purchased 300 and sold one out of four pens at no loss or profit. He sold the remaining pens at a profit of 20%. What is his overall profit or loss percent on the whole transaction?
(a) 15% profit
(b) 15% loss
(c) 12% profit
(d) 12% loss
 View Answer
View Answer 
Ans: a
Pen sold at no loss or no profit 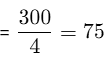
Pens sold at 20% profit = 225
Let CP of one pen = Rs. 1
CP of 225 pens = Rs. 225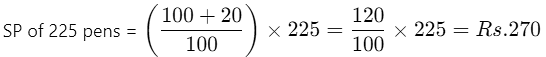 Total CP = Rs. 300Total SP = 270 + 75 = Rs. 345
Total CP = Rs. 300Total SP = 270 + 75 = Rs. 345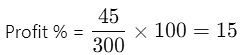
Q47: Answer the following questions and select the correct option:
(i) Abhinav borrowed ₹6000 from a bank for 2 years. If the rate of interest was 10% per annum, then what will be the compound interest if interest is compounded annually?
(ii) Sushant bought a cell phone for ₹x. If the cost of the cell phone in 2 years is depreciated to ₹12,000 at 20% per annum, then find the value of x.
(a) (i) ₹1300; (ii) ₹16,000
(b) (i) ₹960; (ii) ₹17,500
(c) (i) ₹1260; (ii) ₹18,750
(d) (i) ₹1050; (ii) ₹18,000
 View Answer
View Answer 
Ans: (c)
- To calculate the compound interest: - Use the formula: A = P(1 + r/n)^(nt) - Here, P = ₹6000, r = 10% (0.10), n = 1 (compounded annually), t = 2 years. - A = 6000(1 + 0.10/1)^(1*2) = 6000(1.1)^2 = 6000 * 1.21 = ₹7260. - Compound Interest = A - P = ₹7260 - ₹6000 = ₹1260.
- For the depreciation of the cell phone: - The formula for depreciation is: Final Value = Initial Value * (1 - rate)^time. - Here, Final Value = ₹12,000, rate = 20% (0.20), time = 2 years. - So, ₹12,000 = x * (1 - 0.20)^2 = x * 0.64. - Therefore, x = ₹12,000 / 0.64 = ₹18,750. Thus, the answers are (i) ₹1260 and (ii) ₹18,750, which corresponds to option (c).
Q48: Match the expressions in Column - I with their corresponding factors in Column - II and choose the correct option.
(a) (P) → (iii); (Q) → (i); (R) → (iv); (S) → (ii)
(b) (P) → (ii); (Q) → (i); (R) → (iv); (S) → (iii)
(c) (P) → (iii); (Q) → (iv); (R) → (i); (S) → (ii)
(d) (P) → (iii); (Q) → (iv); (R) → (ii); (S) → (i)
 View Answer
View Answer 
Ans: (a)
- To solve this matching question, we need to factor each expression in Column - I.
- For (P) 16x² - 9, it factors to (4x - 3)(4x + 3), which corresponds to (iii).
- For (Q) 5x² + 32x + 35, it factors to (5x + 7)(x + 5), which corresponds to (i).
- For (R) 7x² + 6x - 16, it factors to (7x - 8)(x + 2), which corresponds to (iv).
- For (S) 9x² + 12x + 4, it factors to (3x + 2)(3x + 2), which corresponds to (ii).
- Thus, the correct matches are (P) → (iii), (Q) → (i), (R) → (iv), (S) → (ii).
Q49. A polyhedron has 7 faces and 10 vertices. How many edges does the polyhedron have?
(a) 15
(b) 17
(c) 10
(d) 2
 View Answer
View Answer 
Ans: (a)
For any polyhedron:
F + V – E = 2
Here, F = 7, V = 10, E = ?
Using above formula,
7+10−E=2⇒17−E=2⇒17−2=E⇒E=15
Q50: Which of the following statement is false?
(a) Sphere has one flat surface.
(b) A cone has one flat face.
(c) A cylinder has one cylinder face.
(d) A sphere has one curved face.
 View Answer
View Answer 
Ans: (a)
Sphere has no flat surface but has one curved surface.
|
42 videos|82 docs|61 tests
|















