Maths Olympiad Model Test Paper -2 | Mathematics Olympiad for Class 9 PDF Download
| Table of contents |

|
| Logical Reasoning |

|
| Mathematical Reasoning |

|
| Everyday Mathematics |

|
| Achievers Section |

|
Note: The questions provided in this document are similar to the questions that were asked in the actual Olympiad exam. So, we recommend you study these for your Olympiad preparation
Logical Reasoning
Q1: The position of how many digits will remain the same, if the digits in the number 97215368 are rearranged in the descending order?
(a) None
(b) One
(c) Two
(d) Three
 View Answer
View Answer 
Ans: (d)
After arranging the numbers in descending order, we get
Descending order 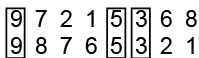
Q2: Three positions of a dice are shown below. Which of the following alphabet is on the face opposite to the face having alphabet B?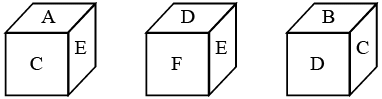 (a) F
(a) F
(b) E
(c) A
(d) C
 View Answer
View Answer 
Ans: (b)
The alphabets on the opposite faces are : (A, D), (B, E) and (C, F)
Q3: Which of the following figures is exactly embedded in the given figure as one of its parts? (a)
(a) 
(b) 
(c) 
(d) 
 View Answer
View Answer 
Ans: (b)
Q4: In a specific coding system, ‘348’ translates to ‘she likes apples’, ‘8375’ translates to ‘parrots likes apples lot’ and ‘748’ translates to ‘she likes parrots’. What is the code for ‘parrots’ in that coding system?
(a) 3
(b) 4
(c) 8
(d) 7
 View Answer
View Answer 
Ans: (d)
- To find the code for ‘parrots’, we analyze the given codes.
- From ‘348’ (she likes apples) and ‘748’ (she likes parrots), we see that ‘8’ represents ‘likes’ and ‘3’ represents ‘she’.
- In ‘8375’ (parrots likes apples lot), since ‘8’ is already known as ‘likes’, we can deduce that ‘7’ must represent ‘parrots’.
- Thus, the code for ‘parrots’ is ‘7’.
Q5: Savita walks 20 m to the West, then turns left and walks 18 m, then again turns left and walks 13 m and then turns right and walks 6 m. How far and in which direction is she now with respect to the starting point?
(a) 25 m, South-East
(b) 25 m, South-West
(c) 24 m, South-East
(d) 20 m, South
 View Answer
View Answer 
Ans: (b)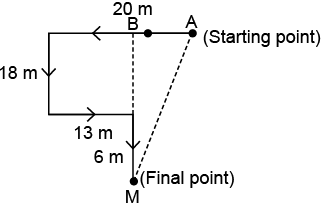
AB = (20 – 13) m = 7 m
BM = (18 + 6) m = 24 m
Now, in ΔABM, using Pythagoras theorem,
AM2 = AB2 + BM2
= 72 + 242
= 49 + 576
= 625
⇒ AM = 25 m
So, Savita is 25 m away and in South-West direction with respect to the starting point.
Q6: Find the odd one out.
(a) 
(b) 
(c) 
(d) 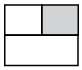
 View Answer
View Answer 
Ans: (c)
Except figure in option (C), all other figures can be obtained by rotating each other.
Q7: Select a figure from the options which satisfies the same conditions of placement of the dots as in the given figure.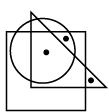 (a)
(a) 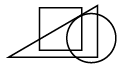
(b) 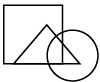
(c) 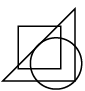
(d) 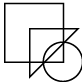
 View Answer
View Answer 
Ans: (d)
Q8: A building has seven floors numbered from one to seven, where the ground floor is labeled as one, the next as two, and so forth, with the topmost floor being seven. Each of the seven individuals, P, Q, R, S, T, U, and V, resides on a different floor. P is on the fourth floor. T is on the floor directly beneath U’s floor. U is not on the second or seventh floor. R occupies the third floor. Q does not live on a floor that is directly above or below R’s floor. S is not on the topmost floor. V does not reside on any floor below T’s floor. Who occupies the topmost floor?
(a) Q
(b) V
(c) T
(d) U
 View Answer
View Answer 
Ans: (b)
- To solve this, we need to determine the arrangement of the individuals on the floors based on the clues provided.
- P is on the fourth floor and R is on the third floor. Since Q cannot be above or below R, Q must be on the first or second floor.
- U cannot be on the second or seventh floor, so U must be on the fifth or sixth floor. This means T is on the fourth or fifth floor.
- Since V cannot be below T, and T is below U, V must be on the seventh floor.
- Thus, the only arrangement that fits all clues is that V lives on the topmost floor (seventh floor).
Q9: If ‘W’ stands for ‘division’, ‘X’ stands for ‘multiplication’, ‘Y’ stands for ‘subtraction’ and ‘Z’ stands for ‘addition’, then which of the following options is correct?
(a) 6 X 20 W 12 Y 7 W 1 = 38
(b) 6 W 20 Y 12 Z 7 X 1 = 57
(c) 6 X 20 W 12 Y 7 Z 1 = 62
(d) 6 Y 20 Z 12 X 7 W 1 = 70
 View Answer
View Answer 
Ans: (d)
Q10: Select a figure from the options which will continue the same series as established by the Problem Figures.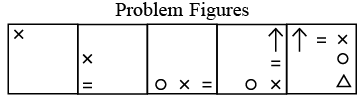 (a)
(a) 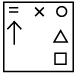
(b) 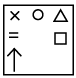
(c) 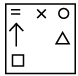
(d) 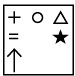
 View Answer
View Answer 
Ans: (c)
Every element moves half and full step alternatively. Also one new element is added at right and left position of the existing element(s) alternatively.
Q11: Find the number which replaces the question mark. 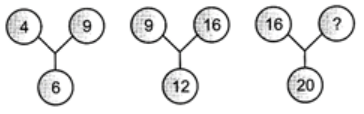 (a) 60
(a) 60
(b) 50
(c) 25
(d) 40
 View Answer
View Answer 
Ans: (c)
Q12: Find the missing number in the following figure.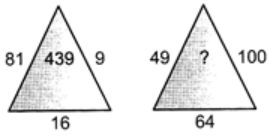 (a) 8710
(a) 8710
(b) 1078
(c) 8107
(d) 789
 View Answer
View Answer 
Ans: (c)
Q13: Find the correct water image of the given figure. (a)
(a) 
(b)
(c) 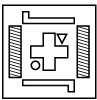
(d) 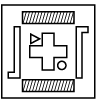
 View Answer
View Answer 
Ans: (b)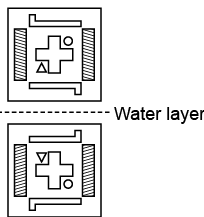
Q14: Study the given information and answer the following question. P ★ Q means P is the father of Q. P # Q means P is the sister of Q. P $ Q means P is the brother of Q. P £ Q means P is the wife of Q. Which of the following means L is the mother of N?
(a) L £ M ★ N
(b) L ★ M £ N
(c) L # M $ O £ N
(d) L £ M ★ O £ N
 View Answer
View Answer 
Ans: (a)
- In the expression L £ M ★ N, L is the wife of M and M is the father of N. This means L is the mother of N.
- The symbol £ indicates that L is the wife, and ★ indicates that M is the father.
- Thus, L being the wife of M and M being the father confirms that L is indeed the mother of N.
- The other options do not correctly represent L as the mother of N based on the given symbols.
15: Identify the pair which is similar to the given pair.
PQ : 1617
(a) EU : 527
(b) EU : 521
(c) JI : 910
(d) KP : 1611
 View Answer
View Answer 
Ans: (b)
Mathematical Reasoning
Q16: If x = k² and y = k is a solution of x - 5y + 6 = 0, then determine the values of k.
(a) 1, 2
(b) 2, 3
(c) 1, 5
(d) 2, 4
 View Answer
View Answer 
Ans: (b)
- Substituting x = k² and y = k into the equation x - 5y + 6 = 0 gives k² - 5k + 6 = 0.
- This is a quadratic equation that can be factored as (k - 2)(k - 3) = 0.
- Setting each factor to zero gives the solutions k = 2 and k = 3.
- Thus, the values of k that satisfy the equation are 2 and 3.
Q17: If (Z - k/2) exactly divides (3z3 - kz2 + 4z + 16), find k.
(a) 4
(b) -4
(c) 2
(d) 0
 View Answer
View Answer 
Ans: (b)
Let f (x) = 3z3 - kz2 + 4z + 16
Then, f (z) will be divisible 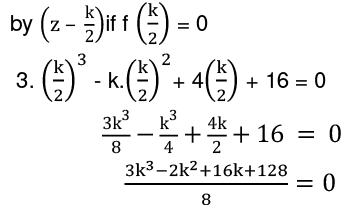
⇒ (k+ 4)(k2 - 4k+ 32)=0
⇒ k + 4 = 0 = k = - 4
Q18: If 3y3 + 8y2 + 8y + 3 + 5k leaves no remainder when divided by y2 + y + 1, what is the value of k?
(a) 0
(b) 5/2
(c) 2/5
(d) -1
 View Answer
View Answer 
Ans: (c)
Let p(x) = 3y3 + 8y2 + 8y + 3 + 5k
- 2 + 5k = 0 (Since, it is given that y2 + y + 1 is a factor of 3y3 + 8y2 + 8y + 3 + 5k, the remainder is equal to 0)
k = 2/5
Q19: As shown in the figure, Given L (4, 6) and M (0, 3) respectively. Find the area of quadrilateral LMOP (in sq. units).2 + 4x + 9, then the remainder when f(x) is divided by (x + 4) is: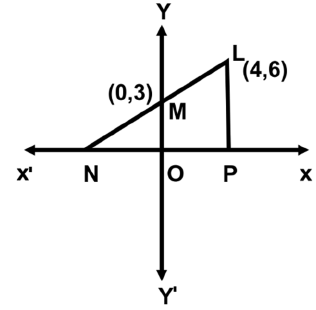 (a) 20
(a) 20
(b) 16
(c) 18
(d) 24
 View Answer
View Answer 
Ans: (c)
Q20: The equation of a line whose x-intercept is -7 and which is parallel to 7x + 10y - 9 = 0 is:
(a) 7x + 10y + 49 = 0
(b) 7x + 10y - 49 = 0
(c) 7x + 10y - 47 = 0
(d) 7x - 10y - 48 = 0
 View Answer
View Answer 
Ans: (a)
Slope of the line parallel to 7x + 10y - 9 = 0 is -7/10
Given that the x-intercept of the required line is -7
It passes through (-7, 0). Hence, the required line is 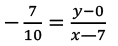
= 7x + 10y + 49 = 0
Q21: The construction of a triangle (△PQR) where PQ = 7 cm and ∠P = 45° can be achieved if (QR + PR) > 7 cm. Which of the following lengths for QR would satisfy this condition?
(a) 6 cm
(b) 7 cm
(c) 8 cm
(d) 5 cm
 View Answer
View Answer 
Ans: (c)
- To construct triangle △PQR, we need to ensure that the sum of the lengths of sides QR and PR is greater than the length of side PQ, which is 7 cm.
- If we take QR as 8 cm, then regardless of the length of PR (as long as it is a positive value), the sum QR + PR will always be greater than 7 cm.
- For example, if QR = 8 cm and PR = 1 cm, then QR + PR = 9 cm, which satisfies the condition.
- In contrast, lengths like 6 cm or 5 cm for QR would not satisfy the condition when added to any positive length for PR.
Q22: Find the product of intercepts of the line 7x + 9y - 63 = 0.
(a) 8
(b) 24
(c) 63
(d) 12
 View Answer
View Answer 
Ans: (c)
7x + 9y - 63 = 0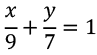
Intercepts are 9 and 7 and their product is 9 x 7 = 63.
Q23: The sum of the digits of a three-digit number is 12. On adding 99, the digits of the number are reversed. The digit in the ten’s place is equal to 1/3 of the sum of the digits in the hundred's place and unit's place. Find the product of the digits in the number.
(a) 60
(b) 40
(c) 36
(d) 70
 View Answer
View Answer 
Ans: (a)
Let the digits in the hundred's place, Ten's place and in the unit's, place be x, y, and z, respectively.
x + y + Z = 12
Given that:
100x + 10y + z + 99 = 100z + 10y + X
99x - 99z =- 99
X - Z =- 1
Given that (x + Z) x (1/3) = y
x + Z = 3y and x + y + Z = 12
⇒ x + z = 12 - y
⇒ 12 -y =3y
⇒ 12 = 4y
⇒ y = 3
⇒ = x + Z = 3 × 3
⇒ x + z = 9
⇒ x - z =- 1
⇒ 2x = 8 ⇒ x = 4 ⇒ z = 5 Product of the digits = 4 x 3 x 5 = 60
Q24: If 4a + 5b + 9c 36, 6a + 15/2 b + 11c = 49. Find c.
(a) 2
(b) 1
(c) 3
(d) Cannot be determined
 View Answer
View Answer 
Ans: (a)
3(4a + 5b + 9c) = (36)3
⇒12a + 15b + 27c = 108 ...........(1) 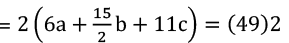
(1) - (2) ⇒ 5c = 10 ⇒ c = 2
Q25: Factorise: (x + y + z)² – (x – y – z)² + 4y² – 4z²
(a) (x + 2z) (4x + y - z)
(b) (x + z) (x + y - 2z)
(c) 4(y + z) (x + y - z)
(d) 2(x + z) (y - 2z)
 View Answer
View Answer 
Ans: (c)
- To factorise the expression, we start with the difference of squares: (x + y + z)² – (x – y – z)².
- This simplifies to 4y(x + z) using the identity a² - b² = (a - b)(a + b).
- Next, we combine this with the remaining terms: 4y(x + z) + 4y² - 4z².
- Factoring out 4 gives us 4[(y + z)(x + y - z)], which leads us to the final factorisation: 4(y + z)(x + y - z).
Q26: The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle if
(a) PQRS is a rectangle
(b) PQRS is a parallelogram
(c) Diagonals of PQRS are equal
(d) Diagonals of PQRS are at right angles
 View Answer
View Answer 
Ans: (d)
Q27: Study the diagram given below and find the value of x if y = 24°.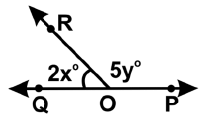 (a) 45o
(a) 45o
(b) 30o
(c) 60o
(d) 50o
 View Answer
View Answer 
Ans: (b)
We know that they are linear angle.
So, 2x°+ 5y° = 180°
Given: y = 24°
So, 2x° = 180 - 5 × 24 2x° = 180 - 120
x° = 60/2 = 30°
Q28: Determine the median and mode of the following set of numbers:
24, 17, 24, 26, 13, 18, 25, 19, 16, 20, 28
(a) 20, 24
(b) 20, 20
(c) 18, 24
(d) 16, 25
 View Answer
View Answer 
Ans: (a)
- To find the median, first, arrange the numbers in ascending order: 13, 16, 17, 18, 19, 20, 24, 24, 25, 26, 28. Since there are 11 numbers, the median is the 6th number, which is 20.
- To find the mode, identify the number that appears most frequently. Here, 24 appears twice, more than any other number, making it the mode.
- Thus, the median is 20 and the mode is 24.
Q29: Some families with pets were surveyed, and the following data was recorded: (Table Based Question) Number of pets in the family and Number of families. If a family is selected at random, what is the probability that it has at least one pet?
(a) 17/25
(b) 18/25
(c) 12/41
(d) 36/25
 View Answer
View Answer 
Ans: (b)
- To find the probability of a family having at least one pet, we first need to determine the total number of families surveyed.
- Next, we count the families that have at least one pet. This includes all families except those with zero pets.
- The probability is then calculated as the number of families with at least one pet divided by the total number of families.
- In this case, the probability comes out to be 18 out of 25 families, which simplifies to 18/25.
Q30: In a △ABC, ∠A = 90o, AB = 5 cm and AC = 12 cm. If AD⊥BC, then the length of AD is:
(a) 60/13 cm
(b) 13/2 cm
(c) 13/60 cm
(d) 2/13 cm
 View Answer
View Answer 
Ans: (a)
Q31: In the given figure, if BC || FE and AB : AF = 2 : 5 and CE = 21 cm, then the length of AC is: 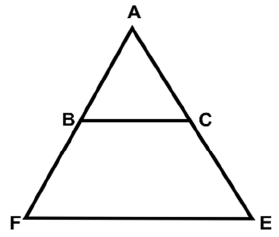
(a) 16 cm
(b) 18 cm
(c) 14 cm
(d) 15 cm
 View Answer
View Answer 
Ans: (c)
By basic proportionality theorem: 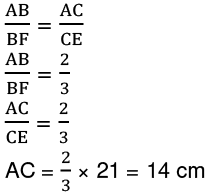
Q32: In a ΔABC, D and E are the points on the sides AB and AC, and D is the midpoint of AB. DE is parallel to BC. F is the midpoint of AE and G is a point on AD such that GF is parallel to DE. If BC = 12 cm, then what is the length of GF in cm?
(a) 3 cm
(b) 2 cm
(c) 5 cm
(d) 6 cm
 View Answer
View Answer 
Ans: (a)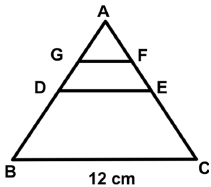
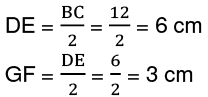
Q33: In the given figure, DE||BC, AD = 5 cm, BC = 6 cm, and DE = 2 cm. Find DB.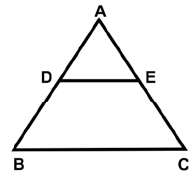 (a) 5 cm
(a) 5 cm
(b. 7.5 cm
(c. 10 cm
(d. 15 cm
 View Answer
View Answer 
Ans: (c)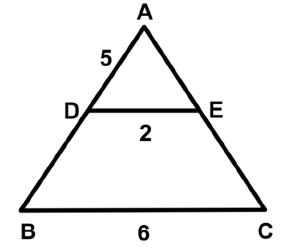
Q34: In the given figure, ABC is an isosceles triangle AB = AC. BD and CD are external bisectors of ∠B and ∠C, respectively. They meet at D. If ∠ABC = 70°, then ∠BDC = ______.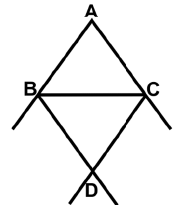 (a) 40o
(a) 40o
(b) 70o
(c) 100o
(d) 80o
 View Answer
View Answer 
Ans: (b)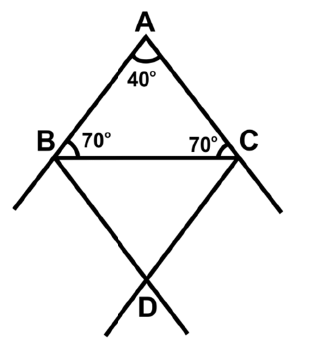 In ∆ABC, AB = AC.
In ∆ABC, AB = AC.
∠ABC = ∠ACB and
∠ACB = ∠ABC = 70° (given)
In ∆BCD, ∠BDC = 180° - (∠DBC + ∠DCB)
∠BDC = 70°
Q35: The length of a hall is 20 m and the width is 16 m. The total area of the floor and the roof equals the total area of the four walls. What is the height of the hall?
(a) 6.45 m
(b) 7.18 m
(c) 8.89 m
(d) 9.20 m
 View Answer
View Answer 
Ans: (c)
- To find the height of the hall, we first calculate the area of the floor and the roof. The area of the floor is length × width = 20 m × 16 m = 320 m². Since the roof has the same area, the total area of the floor and roof is 320 m2 + 320 m2 = 640 m2.
- Next, we calculate the area of the four walls. The area of the walls is given by the formula: 2 × (length + width) × height. This equals 2 × (20 m + 16 m) × height = 72 m × height.
- According to the problem, the area of the floor and roof (640 m²) equals the area of the walls (72 m × height). Setting these equal gives us the equation: 640 = 72 × height.
- Solving for height, we find height = 640 / 72 = 8.89 m.
Everyday Mathematics
Q36: In the given figure (not to scale), AB = 3 cm and CD = 4 cm. The perimeter of the quadrilateral ABCD is _______.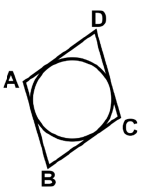 (a) 12 cm
(a) 12 cm
(b) 10 cm
(c) 14 cm
(d) 9 cm
 View Answer
View Answer 
Ans: (c)
AP = AS, BS = BR, CR = CQ, and DQ = DP
(Since Tangents drawn from an external point to a circle are equal.) 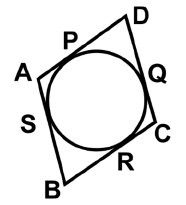
Q37: 12 years ago, the ratio of the ages of P to Q was 3 : 4. Currently, P's age is (3 3/5) times R's age. If R is now 10 years old, what is Q's current age?
(a) 32 years
(b) 48 years
(c) 44 years
(d) 58 years
 View Answer
View Answer 
Ans: (c)
- 12 years ago, the ratio of ages of P and Q was 3:4. This means if P was 3 parts, Q was 4 parts.
- Let’s say 12 years ago, P's age was 3x and Q's age was 4x. So, currently, P is 3x + 12 and Q is 4x + 12.
- We know that P's current age is (3 3/5) times R's age. Since R is 10 years old, P's age is (3 3/5) * 10 = 36 years.
- Now, we can set up the equation: 3x + 12 = 36, which gives us 3x = 24, so x = 8.
- Now, Q's current age is 4x + 12 = 4(8) + 12 = 32 + 12 = 44 years.
Q38: The average marks in Mathematics of a class of 24 students is 56. If the marks of 3 students were misread as 44, 45, and 61 instead of the actual marks 48, 59, and 67 respectively. What would be the correct average marks of the class?
(a) 57
(b) 57.5
(c) 55
(d) 56.5
 View Answer
View Answer 
Ans: (a)
- First, calculate the total marks based on the average: 24 students * 56 average = 1344 total marks.
- Next, find the incorrect total by adding the misread marks: 44 + 45 + 61 = 150.
- Now, calculate the correct total by replacing the misread marks with the actual marks: 48 + 59 + 67 = 174.
- So, the correct total marks = 1344 - 150 + 174 = 1368.
- Finally, to find the correct average, divide the correct total by the number of students: 1368 / 24 = 57.
Q39: If a town's population is declining by 15% each year and currently has 32,000 residents, what will the population be in 3 years
(a) 21,454
(b) 18,042
(c) 19,652
(d) 19,008
 View Answer
View Answer 
Ans: (c)
- To find the population after 3 years, we use the formula for exponential decay: Future Population = Present Population × (1 - Rate of Decrease)^Number of Years.
- Here, the present population is 32,000, the rate of decrease is 15% (or 0.15), and the number of years is 3.
- Calculating it: Future Population = 32,000 × (1 - 0.15)^3 = 32,000 × (0.85)^3 ≈ 19,652.
- Thus, the population after 3 years will be approximately 19,652.
Q40: In a cricket match, a batsman hits the boundary 5 times out of 40 balls played by him. What is the probability that a boundary is not hit by a ball?
(a) 1/8
(b) 5/8
(c) 3/4
(d) 7/8
 View Answer
View Answer 
Ans: (d)
- The batsman hits a boundary 5 times out of 40 balls.
- This means he does not hit a boundary 35 times (40 - 5 = 35).
- The probability of not hitting a boundary is calculated as the number of non-boundary hits divided by the total number of balls: 35/40.
- Simplifying 35/40 gives 7/8, which is the correct answer.
Q41: A person needs to fully distribute three colors of paint: 162 liters of red paint, 126 liters of blue paint, and 180 liters of yellow paint into cans of the same size without mixing the colors. What is the minimum number of cans needed?
(a) 24
(b) 26
(c) 28
(d) 30
 View Answer
View Answer 
Ans: (b)
- To find the least number of cans, we first need to determine the greatest common divisor (GCD) of the three amounts of paint: 162, 126, and 180.
- The GCD of these numbers is 18. This means each can should hold 18 liters of paint.
- Now, we divide each amount of paint by the can size: 162/18 = 9 cans for red, 126/18 = 7 cans for blue, and 180/18 = 10 cans for yellow.
- Adding these gives us a total of 9 + 7 + 10 = 26 cans required.
Q42: A taxi charges ₹ 25 for the first kilometer and ₹ 12.50 for every subsequent kilometer. For a distance of p km, an amount of ₹ q is paid. Which of the following shows the linear equation representing the given information?
(a) 12.50 p – 12.50 = 1
(b) 25 – 12.50 p = q
(c) 25 + 12.50 p = q
(d) 12.50 p + 12.50 = q
 View Answer
View Answer 
Ans: (c)
- The taxi fare starts with a fixed charge of ₹ 25 for the first kilometer.
- For every additional kilometer, the charge is ₹ 12.50.
- Thus, for a total distance of p kilometers, the total fare can be expressed as 25 + 12.50(p - 1), which simplifies to 25 + 12.50p - 12.50.
- This leads to the equation 25 + 12.50p = q, which correctly represents the total fare paid.
Q43: The perimeter of a triangular field is 540 m and its sides are in the ratio 25:17:12. Calculate the cost of ploughing the field at ₹ 5 per m2.
(a) ₹ 45,000
(b) ₹ 50,000
(c) ₹ 48,500
(d) ₹ 42,500
 View Answer
View Answer 
Ans: (a)
- First, find the total parts of the ratio: 25 + 17 + 12 = 54 parts.
- Next, calculate the length of each side: - Side 1 = (25/54) * 540 = 250 m, - Side 2 = (17/54) * 540 = 170 m, - Side 3 = (12/54) * 540 = 120 m.
- Now, find the area of the triangle using Heron's formula: - Semi-perimeter (s) = 540/2 = 270 m, - Area = √[s(s-a)(s-b)(s-c)] = √[270(270-250)(270-170)(270-120)] = 2700 m².
- Finally, calculate the cost of ploughing: - Cost = Area * Rate = 2700 m2 * ₹ 5 = ₹ 13,500.
Q44: The marked price of a shirt is 20% higher than the cost price. A discount of 20% is given on the marked price. Find the loss or gain percent.
(a) 4% gain
(b) 4% loss
(c) 2% gain
(d) 2% loss
 View Answer
View Answer 
Ans: (b)
- Let the cost price (CP) of the shirt be 100.
- The marked price (MP) is 20% higher, so MP = 100 + 20% of 100 = 120.
- A 20% discount on the marked price means the selling price (SP) = MP - 20% of MP = 120 - 24 = 96.
- Now, to find the loss percent, we calculate: Loss = CP - SP = 100 - 96 = 4.
- The loss percent is (Loss/CP) * 100 = (4/100) * 100 = 4%.
Q45: A begins a business with an investment of ₹ 6000, and B enters the business 4 months later with ₹ 8000. After one year, they make a profit of ₹ 34,000. What is A's share of the profit?
(a) ₹ 18,000
(b) ₹ 16,000
(c) ₹ 19,000
(d) ₹ 15,000
 View Answer
View Answer 
Ans: (a)
- To determine A's share of the profit, we first calculate the capital contribution of both A and B over the time they invested.
- A invests ₹ 6000 for 12 months, giving a total contribution of ₹ 6000 * 12 = ₹ 72,000.
- B invests ₹ 8000 for 8 months (since he joins 4 months later), resulting in ₹ 8000 * 8 = ₹ 64,000.
- The total capital contribution is ₹ 72,000 + ₹ 64,000 = ₹ 136,000.
- A's share of the profit is then calculated as (A's contribution / Total contribution) * Total profit = (₹ 72,000 / ₹ 136,000) * ₹ 34,000 = ₹ 18,000.
Achievers Section
Q46: ABCD is a trapezium inscribed in a circle and PQRS is the quadrilateral formed by joining the midpoints of AB, BC, CD, and DA in order. If AC = 15 cm, then find the perimeter of quadrilateral PQRS (in cm).
(a) 30
(b) 20
(c) 15
(d) 25
 View Answer
View Answer 
Ans: (a)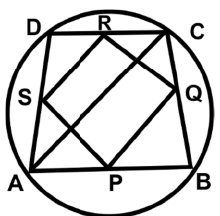 In △ABC, PQ = (1/2) AC, and in △ADC, SR = (1/2) AC.
In △ABC, PQ = (1/2) AC, and in △ADC, SR = (1/2) AC.
So, PQ + SR = AC
In an isosceles trapezium, the diagonals are equal.
So, SP + RQ = AC
So, PQ + QR + RS + SP = 2AC = 30 cm
Q47: VXYZ is a parallelogram and A is a point on VZ. If AYZ is an equilateral triangle and VZ = 2YZ, find ∠XAY.
(a) 100o
(b) 120o
(c) 90o
(d) 110o
 View Answer
View Answer 
Ans: (c)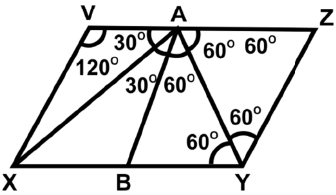
VXYZ is a parallelogram and AYZ is an equilateral triangle. VZ = 2YZ = 2AZ
A is the midpoint of VZ. Join AB such that AB || VX.
Now VABX and ABYZ are two congruent rhombuses.
∠VAB = 60°⇒ ∠XAB = 30°
∠BAZ = 120°⇒ ∠BAY = 60°
So, ∠XAY = 30° + 60° = 90°
Q48: It has been given that JKLM is a quadrilateral. If JL and KM bisect each other, find out what kind of quadrilateral is JKLM?
(a) Square
(b) Rectangle
(c) Parallelogram
(d) Rhombus
 View Answer
View Answer 
Ans: (c)
Since diagonals of a parallelogram bisect each other, JKLM must be a parallelogram.
Q49: Find the sum of the number of diagonals in a 23-sided figure and a 21-sided figure.
(a) 468
(b) 419
(c) 489
(d) 469
 View Answer
View Answer 
Ans: (b)
Number of diagonals of an n-sided polygon = 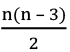
21-sided figure = n = 21
So, diagonals = 189
23-sided figure = n = 23
So, diagonals = 230
Sum = 189 + 230 = 419
Q50: In the following figure, CB is produced to point A. Find ∠CDE.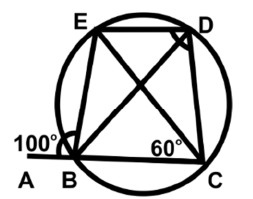
(a) 40o
(b) 100o
(c) 150o
(d) 60o
 View Answer
View Answer 
Ans: (b)
We know that: Exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.
∠ CDE =∠ABE
∠ ABE is given 100°
So, ∠CDE = 100°
|
25 videos|117 docs|45 tests
|
FAQs on Maths Olympiad Model Test Paper -2 - Mathematics Olympiad for Class 9
| 1. What topics are generally covered in the Class 9 Maths Olympiad Model Test Paper -2? |  |
| 2. How can I prepare effectively for the Class 9 Maths Olympiad? |  |
| 3. What is the importance of Logical Reasoning in the Maths Olympiad? |  |
| 4. Are there specific strategies to tackle Everyday Mathematics questions in the Olympiad? |  |
| 5. How is the Achievers Section different from other sections in the Maths Olympiad? |  |















